Построение поля комплексных чисел
Вопрос расширения числовой области неоднократно возникал перед математиками прошлых веков в связи с возникающими новыми задачами. Так было при переходе к рациональным числам от множества натуральных, от рациональных к вещественным и, наконец, от вещественных к комплексным. Дальнейшее расширение оказалось невозможным при сохранении естественных свойств предыдущей числовой области. В случае с комплексными числами вопрос расширения кратко выглядит так: требуется иметь в своем распоряжении возможность решать уравнение
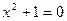 ,
,
которое в вещественной области неразрешимо. С такой задачей столкнулись в позднем средневековье при решении алгебраических уравнений. История эта достаточно интересна и содержит определенную интригу. Признание комплексных чисел затянулось на века, но в данном случае речь пойдет об утилитарной проблеме построения множества комплексных чисел 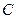 , для которого выделим следующие требования:
, для которого выделим следующие требования:
1. 
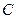 является полем;
является полем;
2.  Поле
Поле  является подполем поля
является подполем поля 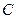 ;
;
3.  Уравнение
Уравнение 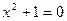 разрешимо в
разрешимо в 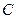 ;
;
4. 
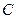 минимально по включению.
минимально по включению.
Такова программа построения новой числовой области.
Определение 2.1. Множеством комплексных чисел называется множество 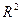 упорядоченных пар вещественных чисел при условии выполнения следующих требований:
упорядоченных пар вещественных чисел при условии выполнения следующих требований:
1. 
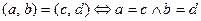 ;
;
2. 
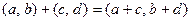 ;
;
3. 
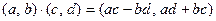 .
.
Таким образом, утверждается критерий равенства пар, а также задаются правила сложения и умножения элементов 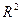 . Покажем, что указанное множество удовлетворяет требованиям 1
. Покажем, что указанное множество удовлетворяет требованиям 1  – 4
– 4  .
.
Теорема 2.1. 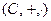 – поле.
– поле.
Доказательство. Во-первых, отметим, что 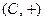 – абелева группа. Операция сложения очевидно алгебраична. Ассоциативность и коммутативность сложения легко следуют из ассоциативности и коммутативности сложения вещественных чисел. Нейтральным элементом, или нулем, является пара
– абелева группа. Операция сложения очевидно алгебраична. Ассоциативность и коммутативность сложения легко следуют из ассоциативности и коммутативности сложения вещественных чисел. Нейтральным элементом, или нулем, является пара 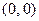 , а противоположной парой к любой данной
, а противоположной парой к любой данной 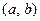 будет, очевидно, пара
будет, очевидно, пара  .
.
Во-вторых, утверждаем, что  тоже абелева группа. Покажем сначала, что операция умножения на множестве
тоже абелева группа. Покажем сначала, что операция умножения на множестве 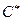 алгебраична. Действительно, пусть
алгебраична. Действительно, пусть 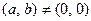 и
и 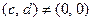 , при этом
, при этом  . Пользуясь условием равенства двух комплексных чисел, находим, что
. Пользуясь условием равенства двух комплексных чисел, находим, что
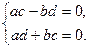
Рассмотрим несколько вариантов. Пусть 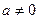 и
и 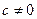 . Тогда и
. Тогда и  , ибо в противном случае
, ибо в противном случае  , что невозможно. Из первого уравнения выразим
, что невозможно. Из первого уравнения выразим 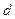 и подставим во второе. Получим эквивалентную систему:
и подставим во второе. Получим эквивалентную систему:
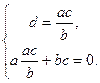
Откуда имеем 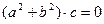 , что невозможно. Если теперь
, что невозможно. Если теперь 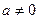 и
и 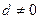 , то опять
, то опять  , а иначе
, а иначе  . Теперь, выражая
. Теперь, выражая 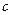 из второго уравнения и подставляя в первое, имеем
из второго уравнения и подставляя в первое, имеем
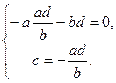
Это влечет  , что тоже невозможно. Аналогично рассматриваются случаи с
, что тоже невозможно. Аналогично рассматриваются случаи с  и
и 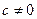 , а также
, а также  и
и 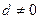 . Таким образом, считаем, что алгебраичность операции умножения пар установлена.
. Таким образом, считаем, что алгебраичность операции умножения пар установлена.
Докажем ассоциативность умножения.
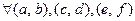 должно быть
должно быть 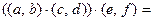
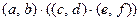 .
.
Вычислим отдельно левую и правую части соотношения.
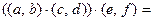
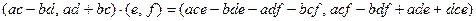 .
.
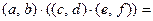
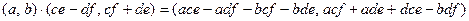 .
.
Как видим, левая и правая части совпадают.
Похожим образом доказывается коммутативность умножения.
Найдем нейтральный элемент. Для этого решим уравнение
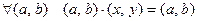 .
.
Уравнение приводит к системе
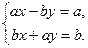
Пусть 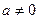 и
и  , тогда умножая первое уравнение на
, тогда умножая первое уравнение на 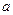 , а второе на
, а второе на  и складывая почленно, получим, что
и складывая почленно, получим, что 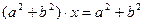 , откуда
, откуда 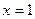 и тогда
и тогда 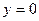 . Легко видеть, что при
. Легко видеть, что при 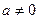 и
и 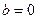 , а также при
, а также при 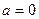 и
и  получаем тот же ответ. Так что единица установлена, это пара
получаем тот же ответ. Так что единица установлена, это пара 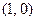 .
.
Осталось указать для любой пары 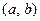 такую пару
такую пару 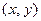 , что
, что 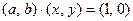 . Это уравнение приводит к системе
. Это уравнение приводит к системе
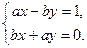
Решая эту систему, вновь предположим, что 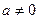 и
и  . Тогда умножая первое уравнение на
. Тогда умножая первое уравнение на 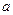 , а второе на
, а второе на  и складывая почленно, получаем, что
и складывая почленно, получаем, что 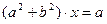 , откуда
, откуда 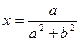 . А отсюда находим, что
. А отсюда находим, что 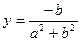 . Итак,
. Итак, 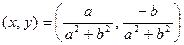 .
.
Если 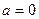 и
и  или
или 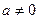 и
и 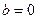 , то справедливой остается полученная формула, доказательство чего оставляем студентам. Таким образом, найден обратный элемент к паре
, то справедливой остается полученная формула, доказательство чего оставляем студентам. Таким образом, найден обратный элемент к паре 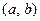 , именно:
, именно: 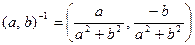 . Значит, наличие мультипликативной группы установлено. Проверку выполнимости дистрибутивного закона также оставляем студентам в качестве упражнения. Тогда
. Значит, наличие мультипликативной группы установлено. Проверку выполнимости дистрибутивного закона также оставляем студентам в качестве упражнения. Тогда 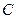 – поле, и теорема доказана.
– поле, и теорема доказана.
Теорема 2.2.  подполе в
подполе в 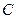 .
.
Доказательство. При доказательстве этого факта воспользуемся приемом, достаточно широко используемым в алгебре. Зададим множество
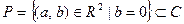 .
.
Покажем, что это множество есть подполе в 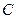 . Действительно, пары вида
. Действительно, пары вида 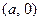 образуют аддитивную абелеву группу относительно сложения пар. Ибо сложение алгебраично: для любых
образуют аддитивную абелеву группу относительно сложения пар. Ибо сложение алгебраично: для любых 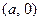 ,
, 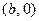
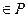
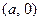 +
+ 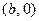
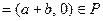 . Пара
. Пара 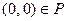 и очевидно, что противоположные пары вида
и очевидно, что противоположные пары вида 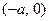 тоже принадлежат
тоже принадлежат  .
.
Операция умножения на 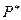 также алгебраична, так как для
также алгебраична, так как для 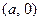 ,
, 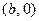
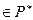
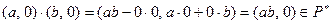 .
.
Единица 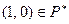 . И, наконец, для каждой пары
. И, наконец, для каждой пары 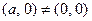 существует пара
существует пара  такая, что
такая, что 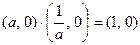 . Проверять выполнимость ассоциативности, коммутативности и дистрибутивности, очевидно, не нужно. Поэтому можно утверждать, что множество
. Проверять выполнимость ассоциативности, коммутативности и дистрибутивности, очевидно, не нужно. Поэтому можно утверждать, что множество  относительно сложения и умножения пар представляет собой поле, подполе поля
относительно сложения и умножения пар представляет собой поле, подполе поля 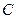 .
.
Зададим отображение 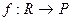 по правилу
по правилу 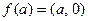
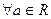 . Ясно, что такое отображение является биекцией. Но кроме этого, оно согласовано с операциями, именно:
. Ясно, что такое отображение является биекцией. Но кроме этого, оно согласовано с операциями, именно:
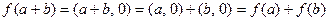
и
 .
.
Значит, отображение 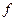 является изоморфизмом. Таким образом, констатируется тот факт, что по своим свойствам операций поля
является изоморфизмом. Таким образом, констатируется тот факт, что по своим свойствам операций поля  и
и  неразличимы. Тогда с помощью модели
неразличимы. Тогда с помощью модели  можно «вложить» поле
можно «вложить» поле  в поле
в поле  . Говорят, что поле
. Говорят, что поле  вложено в поле
вложено в поле 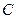 с точностью до изоморфизма. Теорема доказана.
с точностью до изоморфизма. Теорема доказана.
Теорема 2.3. Уравнение 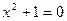 разрешимо в поле
разрешимо в поле 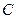 .
.
Доказательство. Перепишем это уравнение как уравнение над 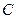 . Имеем
. Имеем
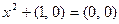 .
.
Предположим, что искомое решение представляет собой пару 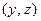 . Тогда, выполняя операции над парами, находим, что
. Тогда, выполняя операции над парами, находим, что
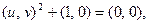
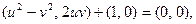
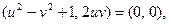
что приводит к системе:
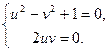
Эта система должна быть решена как система над полем вещественных чисел. Поэтому из нижнего уравнения заведомо 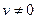 , ибо в таком случае приходим к той задаче, с которой начинали. Пусть тогда
, ибо в таком случае приходим к той задаче, с которой начинали. Пусть тогда 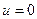 . Тогда первое уравнение дает, что
. Тогда первое уравнение дает, что 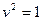 , т.е.
, т.е. 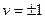 , откуда получаем два комплексных решения:
, откуда получаем два комплексных решения: 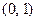 и
и  . Эти корни принято обозначать буквами
. Эти корни принято обозначать буквами 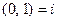 и
и 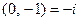 . Иногда их называют мнимыми единицами. Это название носит чисто исторический характер, идущий от эпохи признания-непризнания комплексных чисел. Теорема доказана.
. Иногда их называют мнимыми единицами. Это название носит чисто исторический характер, идущий от эпохи признания-непризнания комплексных чисел. Теорема доказана.
Пусть теперь задано произвольное комплексное число 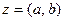 . Запишем его несколько иначе, используя найденные в предыдущей теореме квадратные корни из
. Запишем его несколько иначе, используя найденные в предыдущей теореме квадратные корни из 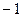 и изоморфизм теоремы 2.2. Имеем
и изоморфизм теоремы 2.2. Имеем
 .
.
Здесь производится отождествление вещественных чисел 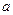 и
и  с парами
с парами 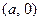 и
и 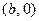 соответственно при помощи изоморфизма
соответственно при помощи изоморфизма 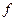 . Надо только помнить, что знаки «+» и « . » означают соответственно операции сложения и умножения пар.
. Надо только помнить, что знаки «+» и « . » означают соответственно операции сложения и умножения пар.
Определение 2.2. Запись комплексного числа  в виде
в виде 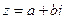 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Определение 2.3. Если комплексное число задано в алгебраической форме 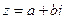 , то число
, то число 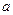 называется вещественной (действительной) частью
называется вещественной (действительной) частью  и обозначается
и обозначается 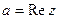 , а число
, а число  называется мнимой частью
называется мнимой частью  и обозначается
и обозначается 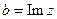 .
.
Отсюда понятно, что можно записать 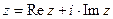 . Сами названия носят тоже исключительно исторический характер, ибо мнимая часть не большая абстракция, нежели вещественная. Подчеркнем, что мнимая часть комплексного числа есть число вещественное. Теперь легко видеть, что если
. Сами названия носят тоже исключительно исторический характер, ибо мнимая часть не большая абстракция, нежели вещественная. Подчеркнем, что мнимая часть комплексного числа есть число вещественное. Теперь легко видеть, что если  , то
, то 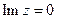 . Комплексные числа с равной нулю вещественной частью часто называют чисто мнимыми и обозначают
. Комплексные числа с равной нулю вещественной частью часто называют чисто мнимыми и обозначают 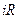 .
.
Теорема 2.4. Поле комплексных чисел минимально по включению.
Доказательство. Пусть поле 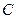 содержит подполе
содержит подполе 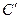 , которое в свою очередь включает поле
, которое в свою очередь включает поле  , т.е.,
, т.е.,
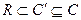 ,
,
и в 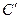 разрешимо уравнение
разрешимо уравнение 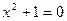 с корнями
с корнями 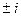 . Тогда в этом новом поле должны содержаться элементы
. Тогда в этом новом поле должны содержаться элементы 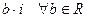 . А тогда
. А тогда 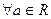 сумма
сумма 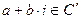 . Но такими элементами исчерпывается поле
. Но такими элементами исчерпывается поле 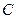 . Следовательно,
. Следовательно, 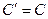 . Теорема доказана.
. Теорема доказана.
Опишем операции над комплексными числами в алгебраической форме.
1. 
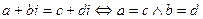 ;
;
2. 
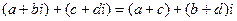 ;
;
3. 
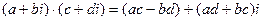 ;
;
4. 
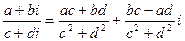 для
для  .
.
Эти формулы позволяют утверждать, что сложение комплексных чисел есть приведение подобных членов для двух двучленов, умножение комплексных чисел есть простое перемножение таких двучленов с одной особенностью, что  . Наконец, деление есть ни что иное, как избавление от числа
. Наконец, деление есть ни что иное, как избавление от числа 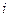 в знаменателе. Последнюю формулу легко получить, умножая числитель и знаменатель указанной дроби на число
в знаменателе. Последнюю формулу легко получить, умножая числитель и знаменатель указанной дроби на число 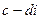 . Отсюда, кстати, следует, что нет нужды в специальном заучивании таких формул.
. Отсюда, кстати, следует, что нет нужды в специальном заучивании таких формул.
Комплексное сопряжение
Определение 2.4. Пусть 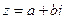 , тогда число
, тогда число 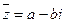 называется сопряженным с числом
называется сопряженным с числом  (точнее, комплексно сопряженным).
(точнее, комплексно сопряженным).
Рассмотрим свойства комплексно сопряженных чисел. Здесь 
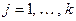 .
.
1. 
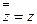 ;
;
2. 
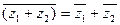 ;
;
3. 
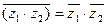 ;
;
4. 
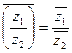 ,
, 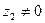 ;
;
5. 
 ;
;
6. 
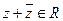 ;
;
7. 
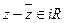 ;
;
8. 
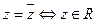 ;
;
Свойства 2  и 3
и 3  допускают естественные обобщения.
допускают естественные обобщения.
9. 
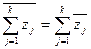 для
для 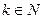 ;
;
10. 
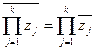 для
для 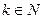 .
.
Докажем свойство 9  в предположении, свойство 2
в предположении, свойство 2  доказано. Это будет база индукции. Предполагаем, что свойство доказано для всех
доказано. Это будет база индукции. Предполагаем, что свойство доказано для всех 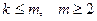 . Докажем, что оно справедливо для
. Докажем, что оно справедливо для 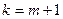 . Имеем
. Имеем
 .
.
Доказательство десятого свойства повторяет доказательство девятого, а справедливость остальных проверяется тривиально. Теперь можно сказать, что при операции деления двух комплексных чисел числитель и знаменатель дроби умножаются на число сопряженное со знаменателем.
Геометрическая интерпретация комплексных чисел
Зададим на плоскости декартову систему координат. Саму плоскость назовем комплексной плоскостью, ось абсцисс ОХ назовем вещественной осью, а ось ординат 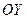 – мнимой. Зафиксируем комплексное число
– мнимой. Зафиксируем комплексное число 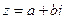 и в данной системе координат представим точку
и в данной системе координат представим точку  . Так как каждая точка плоскости имеет вполне определенные координаты в указанной системе, выражающиеся упорядоченной парой вещественных чисел, то тем самым можно поставить в соответствие эту точку числу
. Так как каждая точка плоскости имеет вполне определенные координаты в указанной системе, выражающиеся упорядоченной парой вещественных чисел, то тем самым можно поставить в соответствие эту точку числу  . С другой стороны, комплексное число, как упорядоченная пара вещественных чисел, может однозначно изображаться точкой комплексной плоскости в данной системе координат. Следовательно, легко установить биективное отображение
. С другой стороны, комплексное число, как упорядоченная пара вещественных чисел, может однозначно изображаться точкой комплексной плоскости в данной системе координат. Следовательно, легко установить биективное отображение 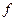 множества комплексных чисел на множество точек комплексной плоскости, выражающееся равенством:
множества комплексных чисел на множество точек комплексной плоскости, выражающееся равенством:
 , или
, или 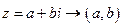 .
.
Это отображение задает т.н., точечную геометрическую интерпретацию комплексных чисел.
Рассмотрим теперь множество векторов- направленных отрезков комплексной плоскости, начала которых закреплены в точке О, начале координат. Конец каждого такого вектора лежит в некоторой точке той же плоскости, и эта точка однозначно определяет положение вектора. Пусть конец вектора лежит в точке  , тогда можно установит биективное отображение множества комплексных чисел на множество указанных векторов по правилу: любое комплексное число
, тогда можно установит биективное отображение множества комплексных чисел на множество указанных векторов по правилу: любое комплексное число 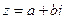 отображается в вектор, конец которого имеет координаты
отображается в вектор, конец которого имеет координаты  . Это отображение задает векторную геометрическую интерпретацию комплексных чисел. В зависимости от характера возникающих задач пользуются той или иной интерпретацией. В любом случае, на вещественной оси отмечается вещественная часть комплексного числа, а на мнимой – мнимая. Удобство такого представления чисел будет показано ниже.
. Это отображение задает векторную геометрическую интерпретацию комплексных чисел. В зависимости от характера возникающих задач пользуются той или иной интерпретацией. В любом случае, на вещественной оси отмечается вещественная часть комплексного числа, а на мнимой – мнимая. Удобство такого представления чисел будет показано ниже.
Определение 2.5. Модулем комплексного числа 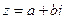 (обозначение:
(обозначение: 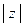 )называется арифметический корень квадратный из суммы квадратов его вещественной и мнимой части, т.е.,
)называется арифметический корень квадратный из суммы квадратов его вещественной и мнимой части, т.е.,
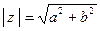 ,
,
или
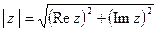 .
.
Как легко видеть, 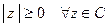 и
и 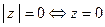 .Кроме того,
.Кроме того, 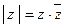 . Геометрически модуль можно интерпретировать как длину вектора, изображающего данное число на комплексной плоскости в векторной интерпретации.
. Геометрически модуль можно интерпретировать как длину вектора, изображающего данное число на комплексной плоскости в векторной интерпретации.
Определение 2.6. Аргументом комплексного числа называется величина угла, который образует вектор, изображающий это число на комплексной плоскости, с вещественной осью. Аргумент считается положительным, если отсчитывается от оси против часовой стрелки, и отрицательным в противном случае.
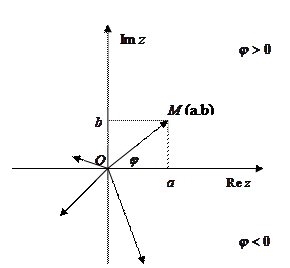

Заметим, прежде всего, что число 0 аргумента не имеет, ибо не определено направление соответствующего вектора. Кроме того, понятно, что аргумент определен неоднозначно, а с точностью до слагаемого 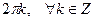 . Поэтому часто используются такие обозначения:
. Поэтому часто используются такие обозначения: 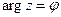 для
для 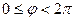 (иногда,
(иногда,  ),
), 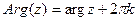 ,
, 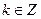 . В последнем случае речь идет о некотором аргументе, представленном в общем виде.
. В последнем случае речь идет о некотором аргументе, представленном в общем виде.
Пример 2.1. 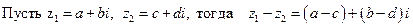 . Тогда
. Тогда
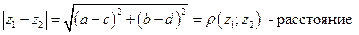 между точками (числами
между точками (числами 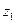 и
и  ) на комплексной плоскости.
) на комплексной плоскости.

Таким образом, модуль разности всегда можно интерпретировать как расстояние.
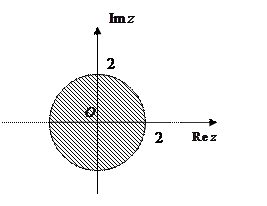
Пример 2.2. Нарисовать на комплексной плоскости область, удовлетворяющую следующему условию: 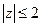 .
.
Положим 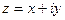 . Тогда
. Тогда 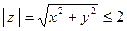 . Таким образом, расстояние от начала координат до любой точки описываемой области не должно превосходить 2. Тогда имеем:
. Таким образом, расстояние от начала координат до любой точки описываемой области не должно превосходить 2. Тогда имеем:
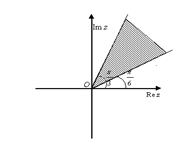
Пример 2.3. Нарисовать на комплексной плоскости область, удовлетворяющую следующему условию:  . Получаем бесконечную угловую область:
. Получаем бесконечную угловую область:
Введем теперь еще одно представление комплексных чисел. Пусть 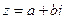 ,
, 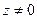 и
и 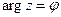 . Рассмотрим описание числа
. Рассмотрим описание числа  в векторной форме.
в векторной форме.

Легко видеть, что можно записать следующие выражения: 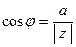 и
и 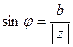 .
.
Иначе, 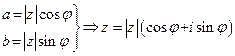 .
.
Определение 2.6. Пусть 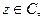
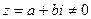 и
и 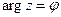 . Тогда представление числа
. Тогда представление числа  в виде
в виде 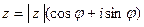 называется тригонометрической формой этого комплексного числа.
называется тригонометрической формой этого комплексного числа.
Замечание. Тригонометрической формой называется только указанная запись. Любое другое представление числа  , содержащее значения тригонометрических функций, таковым не является. Обычно обозначают
, содержащее значения тригонометрических функций, таковым не является. Обычно обозначают 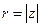 и тогда
и тогда
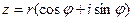 .
.
Пример 2.4. Запишем несколько чисел в тригонометрической форме:
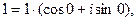
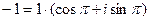 ,
,
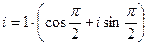 ,
,
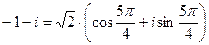 ,
,
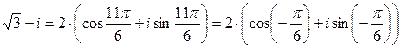 .
.
Рассмотрим действия над комплексными числами в тригонометрической форме. Если сложение и вычитание производятся так же, как и в алгебраической форме, то умножение и деление гораздо проще. Но предварительно надо отметить условие равенства. Пусть заданы два числа 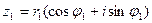 и
и  . Тогда
. Тогда
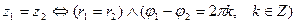 .
.
Лемма 2.1. Если 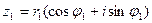 и
и 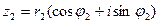 , то
, то
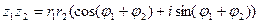 .
.
Доказательство. Перемножая указанные два числа обычным образом (как в алгебраической форме), имеем:
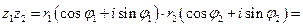
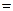
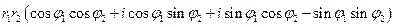 .
.
Теперь группируя слагаемые и применяя тригонометрические формулы для синуса и косинуса суммы аргументов, получаем требуемое. Лемма доказана.
Следствие. 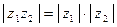 ,
,
 .
.
Лемма 2.2. Если 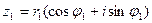 и
и 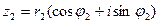 , то
, то
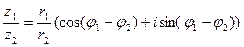 .
.
Доказательство.
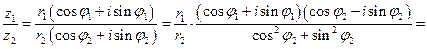
 .
.
Здесь воспользовались результатом предыдущей леммы. Лемма доказана.
Следствие. 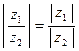 ,
,
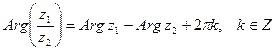 .
.
Из формулы умножения легко получается формула, описывающая возведение комплексного числа в степень.
Теорема 2.5 (формула Муавра).
Пусть 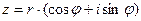 ,
, 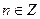 . Тогда имеет место формула
. Тогда имеет место формула
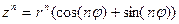 .
.
Доказательство. Пусть сначала 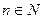 . Проведем доказательство индукцией по
. Проведем доказательство индукцией по  . Содержательный смысл индуктивного рассуждения начинается с
. Содержательный смысл индуктивного рассуждения начинается с 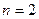 . Будем считать это базой индукции. Действительно,
. Будем считать это базой индукции. Действительно,
 .
.
Предположим, что теорема справедлива для всех натуральных 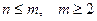 и докажем справедливость формулы для
и докажем справедливость формулы для 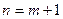 . Имеем
. Имеем
 .
.
Так как для 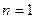 формула тривиальна, а для
формула тривиальна, а для 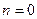 естественно считать
естественно считать 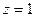 , или
, или

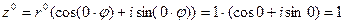 ,
,
то теорема справедлива для всех неотрицательных целых показателей. Докажем теперь формулу для отрицательных показателей. Пусть вновь 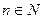 , тогда
, тогда
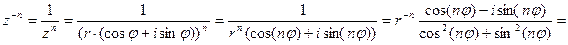
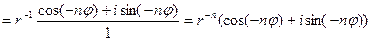 .
.
Таким образом, теорема справедлива для любого целого  .
.
Следствие. 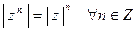 ,
,
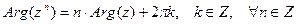 .
.
Как видим, в качестве следствий получили равенства для модулей произведения и частного двух комплексных чисел. Для суммы и разности удается доказать лишь неравенство.
Теорема 2.6.
Пусть 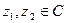 . Тогда имеет место следующее неравенство:
. Тогда имеет место следующее неравенство:
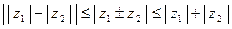 .
.
Доказательство. Если какое-либо из чисел 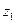 или
или  равно нулю, то неравенство становится тривиальным. Поэтому считаем, что
равно нулю, то неравенство становится тривиальным. Поэтому считаем, что 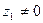 и
и 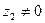 . Значит, эти числа можно представить в тригонометрической форме. Пусть
. Значит, эти числа можно представить в тригонометрической форме. Пусть
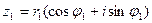 и
и 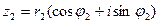 .
.
Докажем правую часть неравенства. Имеем
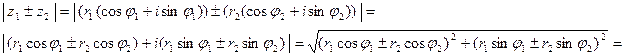
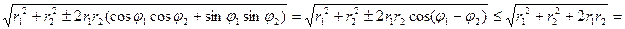
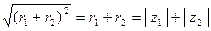 .
.
Здесь учли, что 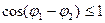 .
.
Левая часть неравенства доказывается похожим образом, что оставляем студентам.
Следствие. Равенство в указанном неравенстве достигается тогда и только тогда, когда 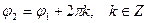 .
.
Извлечение корня из комплексного числа.
Определение 2.7. Пусть 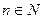 и
и 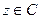 , тогда корнем степени
, тогда корнем степени  из комплексного числа
из комплексного числа  называется комплексное число
называется комплексное число  , удовлетворяющее условию
, удовлетворяющее условию  .
.
Сразу заметим, что если 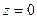 , то очевидно, что
, то очевидно, что 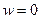 . Поэтому будем считать, что
. Поэтому будем считать, что 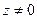 . Покажем, что корни степени
. Покажем, что корни степени  из числа
из числа  существуют. Представим
существуют. Представим  в тригонометрической форме:
в тригонометрической форме: 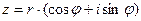 и сначала предположим, что искомые корни действительно существуют. Пусть
и сначала предположим, что искомые корни действительно существуют. Пусть  . Тогда по формуле Муавра имеем
. Тогда по формуле Муавра имеем
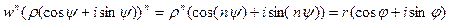 .
.
На основе равенства двух комплексных чисел, записанных в тригонометрической форме, получаем:
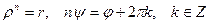 .
.
Отсюда сразу находим, что
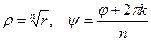 .
.
Тогда можно сконструировать число  , точнее,
, точнее, 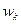 . А именно
. А именно
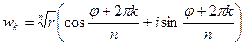 .
.
Оказалось, что корень  -ой степени зависит от параметра
-ой степени зависит от параметра 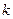 . Уясним точнее эту зависимость.
. Уясним точнее эту зависимость.
Лемма 2.3. 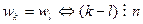 .
.
Доказательство.
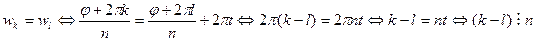 .
.
Построим множество 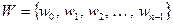 . В силу предшествовавшей леммы элементы этого множества попарно различны. С другой стороны, для любого
. В силу предшествовавшей леммы элементы этого множества попарно различны. С другой стороны, для любого 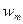 имеем:
имеем:
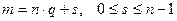 ,
,
откуда немедленно находим, что 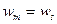 . Отсюда получаем теорему.
. Отсюда получаем теорему.
Теорема 2.7.
Пусть 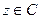 ,
, 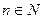 , тогда, если
, тогда, если 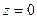 , то имеется единственное значение корня
, то имеется единственное значение корня  -ой степени из этого числа
-ой степени из этого числа 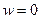 ; если
; если 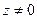 и
и 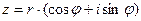 , то имеется ровно
, то имеется ровно  значений корня
значений корня  -ой степени из
-ой степени из  , которые можно получить из следующей формулы:
, которые можно получить из следующей формулы:
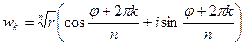 , где
, где 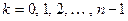 .
.
Следствие. Геометрически (в точечной интерпретации) значения корня  -ой степени из числа
-ой степени из числа  можно представить точками, лежащими на окружности радиуса
можно представить точками, лежащими на окружности радиуса 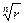 с центром в начале координат и делящими указанную окружность на
с центром в начале координат и делящими указанную окружность на  равных частей.
равных частей.
Пример 2.5. Найдем значения корня четвертой степени из числа  .
.
Запишем число  в тригонометрической форме. Имеем
в тригонометрической форме. Имеем
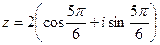 .
.
Тогда значениями коня будут
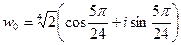 ,
,
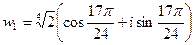 ,
,
 ,
,
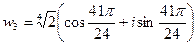 .
.
Применим формулу извлечения корня к частному случаю 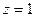 , т.е., рассмотрим вопрос о корнях из единицы. С учетом сложившихся обозначений получим:
, т.е., рассмотрим вопрос о корнях из единицы. С учетом сложившихся обозначений получим:
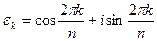 ,
, 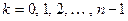 ,
,
так как 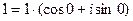 . Опираясь на формулу Муавра легко заметить, что
. Опираясь на формулу Муавра легко заметить, что 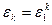 , т.е., можно получить все значения корня
, т.е., можно получить все значения корня  -ой степени, располагая одним числом
-ой степени, располагая одним числом  . Это наблюдение приводит к следующему результату.
. Это наблюдение приводит к следующему результату.
Теорема 2.8.
Пусть  – множество значений корня
– множество значений корня  -ой степени из единицы. Тогда
-ой степени из единицы. Тогда 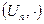 есть мультипликативная циклическая группа порядка
есть мультипликативная циклическая группа порядка  .
.
Доказательство. Во-первых, для любых 
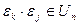 так как
так как 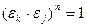 .
.
Число 1 естественно принадлежит  . Наконец, для любого
. Наконец, для любого 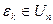 ,
, 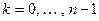 , найдется
, найдется 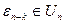 , что
, что 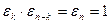 . Цикличность же усматривается наличием числа
. Цикличность же усматривается наличием числа  , что завершает доказательство.
, что завершает доказательство.
Пример 2.6. Пусть 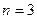 , тогда корнями из 1 третьей степени будут
, тогда корнями из 1 третьей степени будут
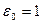 ,
,
 ,
,
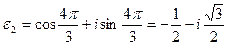 .
.
Пример 2.7. Пусть 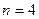 , тогда корнями из 1 четвертой степени будут
, тогда корнями из 1 четвертой степени будут
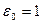 ,
,
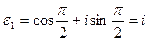 ,
,
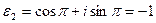 ,
,
 .
.
Пример 2.8. Вычислить значение 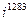 .
.
Разделив число 1283 на 4 получим остаток 3. Тогда
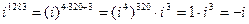 .
.
Определение 2.8. Образующий элемент циклической группы  называется первообразным корнем степени
называется первообразным корнем степени  из единицы.
из единицы.
Как уже было показано, первообразным корнем всегда будет число  , но, вообще говоря, существуют и другие первообразные корни
, но, вообще говоря, существуют и другие первообразные корни  -ой степени (для
-ой степени (для 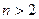 ). Опишем это множество, доказав критерии первообразности. Эти теоремы можно перенести на общий случай циклической группы конечного порядка, сделав соответствующие изменения в терминах. Частично это будет получено в главе XIV.
). Опишем это множество, доказав критерии первообразности. Эти теоремы можно перенести на общий случай циклической группы конечного порядка, сделав соответствующие изменения в терминах. Частично это будет получено в главе XIV.
Теорема 2.9 (первый критерий первообразности).
Корень 
 -ой степени из единицы является первообразным корнем
-ой степени из единицы является первообразным корнем  -ой степени из единицы тогда и только тогда, когда он не является корнем из единицы никакой степени меньшей
-ой степени из единицы тогда и только тогда, когда он не является корнем из единицы никакой степени меньшей  .
.
Доказательство. Необходимость. Докажем результат рассуждением от противного. Пусть  будет первообразным корнем из единицы степени
будет первообразным корнем из единицы степени  и существует
и существует 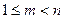 такое, что
такое, что  . Тогда в ряде
. Тогда в ряде 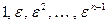 числа начиная с
числа начиная с 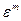 и до
и до 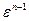 повторяют начальные значения, что противоречит тому, что
повторяют начальные значения, что противоречит тому, что  образующий элемент группы
образующий элемент группы  -го порядка (см. т.1.6). Значит, такого числа
-го порядка (см. т.1.6). Значит, такого числа 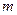 не существует.
не существует.
Достаточность. Пусть теперь корень  не является корнем из единицы никакой степени, меньшей
не является корнем из единицы никакой степени, меньшей  . Тогда в ряде
. Тогда в ряде 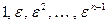 все числа попарно различны, ибо если это не так, то найдутся
все числа попарно различны, ибо если это не так, то найдутся  , откуда для, например,
, откуда для, например, 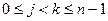
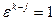 и при этом
и при этом 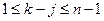 . Таким образом, находится число
. Таким образом, находится число 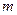 такое, что
такое, что 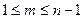 и
и  , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Этот критерий не очень удобен для приложений. Докажем другую теорему, но предварительно потребуется лемма.
Лемма 2.4. Если  есть первообразный корень степени
есть первообразный корень степени  из единицы, то
из единицы, то  тогда и только тогда, когда
тогда и только тогда, когда 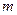 делится на
делится на  .
.
Доказательство. Необходимость. Пусть  – первообразный корень степени
– первообразный корень степени  из единицы и
из единицы и  . Разделим
. Разделим 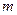 на
на  с остатком:
с остатком: 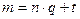 , где
, где 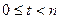 . Тогда
. Тогда
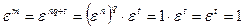 .
.
Отсюда сразу следует, что 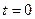 по теореме 2.9.
по теореме 2.9.
Достаточность. Практически очевидна.
Теорема 2.10 (второй критерий первообразности).
Пусть  есть первообразный корень степени
есть первообразный корень степени 
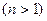 из единицы, тогда
из единицы, тогда 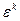 ,
, 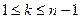 , является первообразным корнем степени
, является первообразным корнем степени  из единицы тогда и только тогда, когда числа
из единицы тогда и только тогда, когда числа  и
и 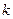 взаимно просты.
взаимно просты.
Доказательство. Необходимость. Пусть 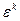 будет первообразным корнем степени
будет первообразным корнем степени  из единицы. Обозначим через
из единицы. Обозначим через 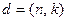 наибольший общий делитель чисел
наибольший общий делитель чисел  и
и 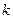 . Это значит, что
. Это значит, что 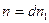 и
и 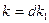 , при этом
, при этом 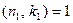 . Тогда имеем
. Тогда имеем
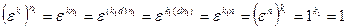 .
.
Если теперь  , т.е.,
, т.е., 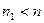 , то получаем противоречие с теоремой 2.9. Значит,
, то получаем противоречие с теоремой 2.9. Значит, 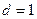 , что и требовалось.
, что и требовалось.
Достаточность. Пусть 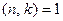 . Рассуждаем от противного. Если
. Рассуждаем от противного. Если 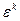 не является первообразным корнем степени
не является первообразным корнем степени  из единицы, то по теореме 2.9 найдется такое
из единицы, то по теореме 2.9 найдется такое 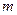 , что
, что 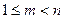 и
и 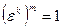 . Тогда
. Тогда 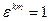 и по лемме 2.4 получаем, что
и по лемме 2.4 получаем, что 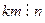 . Но
. Но 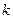 и
и  взаимно просты, поэтому должно быть
взаимно просты, поэтому должно быть 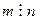 , что невозможно, ибо
, что невозможно, ибо 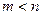 . Значит,
. Значит, 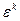 на самом деле является первообразным корнем степени
на самом деле является первообразным корнем степени  из единицы. Теорема доказана.
из единицы. Теорема доказана.
Пример 2.9. Пусть требуется найти первообразные корни степени 12 из единицы. Тогда используя равенство 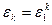 , получим, что, так как числа 1, 5, 7, 11 взаимно просты с числом 12, первообразными корнями двенадцатой степени из единицы наряду с
, получим, что, так как числа 1, 5, 7, 11 взаимно просты с числом 12, первообразными корнями двенадцатой степени из единицы наряду с  будут также и
будут также и 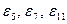 . В то же время ни одно из оставшихся восьми чисел не может быть первообразным корнем степени 12 из единицы. В тригонометрической форме искомые
. В то же время ни одно из оставшихся восьми чисел не может быть первообразным корнем степени 12 из единицы. В тригонометрической форме искомые
можно описать как числа вида
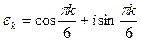 для
для 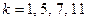 .
.
Теорема 2.11. Все  значений корня
значений корня 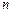 -ой степени из комплексного числа
-ой степени из комплексного числа  можно получить умножением какого-либо одного значения на все значения корня
можно получить умножением какого-либо одного значения на все значения корня 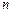 -ой степени из единицы.
-ой степени из единицы.
Доказательство. Пусть  . Рассмотрим множество
. Рассмотрим множество 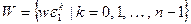 .
.
Очевидно, что числа множества 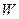 оказываются попарно различными и при этом
оказываются попарно различными и при этом 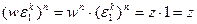 . Теорема доказана.
. Теорема доказана.
Введем еще один вариант записи комплексного числа.
Определение 2.9. Пусть задано комплексное число
