Двоичная, десятичная и шестнадцатеричная системы счисления. Перевод чисел в десятичную систему счисления
Десятичное значение числа, представленного конечной дробью (дробного числа), в n-ичной системе счисления
amam–1…a1a0,a–1a–2…a–k,
где «,» – разделитель целой и дробной частей; ai, i = –k, m; или с явным указанием основания системы счисления
(amam–1…a1a0,a–1a–2…a–k)n,
определяется по формуле
amnm + am–1nm–1 + … + a1n1 + a0n0 +
+ a–1n–1 + a–2n–2 + … + a–kn–k = 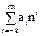 (4.1).
(4.1).
В информатике и вычислительной технике широко используются следующие системы счисления:
- двоичная n = 2; используемый алфавит: A = {0, 1}; например, 01110002;
- десятичная n = 10; используемый алфавит: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; например, 10210; в дальнейшем числа без указания основания системы счисления будем считать десятичными;
- шестнадцатеричная n = 16; используемый алфавит: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}; цифры A, B, C, D, E, F имеют десятичные количественные эквиваленты 10, 11, 12, 13, 14, 15 соответственно; например, AB034D16.
Представление цифр в двоичной, десятичной и шестнадцатеричной системах счисления представлено в табл. 4.1.
Таблица 4.1. Соответствие между цифрами двоичной, десятичной и шестнадцатеричной систем счисления
| Десятичная | Двоичная | Шестнадцатеричная |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
В вычислительной технике используется двоичная система счисления, то есть все числа и данные представляются в виде последовательности нулей и единиц (бит). Двоичная система счисления обладает следующими преимуществами перед системами счисления с другими основаниями:
- для реализации двоичных цифр необходимы технические устройства с двумя устойчивыми состояниями: «ток есть» – «ток отсутствует», «намагничено» – «не намагничено» и т. п., а не с десятью – как в десятичной системе счисления;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- для выполнения арифметических операций используется простой аппарат алгебры высказываний (булевой алгебры).
В вычислительной технике процессы ввода, вывода и обработки числовых данных связаны с преобразованием чисел из одной системы счисления в другую. Поэтому рассмотрим правила перевода чисел одной системы счисления в систему счисления с другим основанием.
В этой главе и далее для каждого правила указывается его номер, краткое название и пример его использования.
Правило 4.1. (перевод целого или дробного числа из n-й системы счисления в десятичную) Число из n-й системы счисления в десятичную переводится по формуле (4.1).
Пример 4.2. Перевести число A50D,0B16 в десятичную систему счисления.
Решение. Используем формулу (4.1):
A×163 + 5×162 + 0×161 + D×160 + 0×16–1 + B×16–2.
Запишем вместо цифр шестнадцатеричной системы счисления их десятичные эквиваленты и выполним операции умножения и сложения:
10×163 + 5×162 + 0×161 + 13×160 + 0×16–1 + 11×16–2 =
= 10×4096 + 5×256 + 13×1 + 11×0,00390625 = 42448,04296875. □
Очевидно, что цифру 0 при переводе чисел можно опускать.
4.3. Перевод целых чисел из одной системы
счисления в другую
Правила перевода числа в другую, не десятичную систему счисления различаются для целых и дробных чисел.
Правило 4.2. (перевод целых чисел из десятичной системы счисления в n-ую систему счисления) Перевод целого числа X осуществляется по следующему алгоритму:
1) получить цифру числа n-ой системы счисления как остаток от деления числа X на основание новой системы счисления n; полученную цифру приписать слева от имеющихся цифр;
2) принять за X частное от деления числа X на основание системы счисления n;
3) выполнять шаги 1-2, пока X ¹ 0.
Пример 4.3. Перевести число 25 в двоичную систему счисления.
Решение. Удобно представить перевод числа в виде столбца
(рис. 4.1), каждая строка которого содержит частное и остаток от деления числа X на основание двоичной системы счисления n = 2.
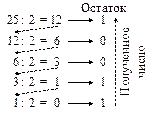
Рис. 4.1. Перевод числа 25 в двоичную систему счисления
В результате получим число 110012 – результат перевода числа 25 в двоичную систему счисления. □
Правило 4.3. (перевод из шестнадцатеричной в двоичную систему счисления) Каждая цифра шестнадцатеричного числа заменяется тетрадой (четырьмя битами), являющейся представлением этой цифры в двоичной системе счисления (табл. 4.1).
Пример 4.4. Перевести число 3BC16 в двоичную систему счисления.
Решение. Цифра 316 представляется числом 00112, B16 – 10112, C16 – 11002. Тогда результат перевода числа 3BC16 в двоичную систему счисления будет равен 0011101111002. □
Правило 4.4. (перевод из двоичной в шестнадцатеричную систему счисления) Двоичное число делится на тетрады справа налево. Каждая тетрада заменяется соответствующей ей цифрой. Если самая левая тетрада неполная, то есть содержит меньше четырех цифр, то слева от числа дописываются нули.
Пример 4.5. Перевести число 11101111002 в шестнадцатеричную систему счисления.
Решение. Разделим число на тетрады и поставим в соответствие каждой тетраде шестнадцатеричную цифру. В самой левой тетраде только две единицы, поэтому дополним ее слева двумя нулями.
| ¯ | ¯ | ¯ |
| ¯ | ¯ | ¯ |
| B | C |
В результате получаем число 3BC16. Данный пример является обратным примеру 4.4, поэтому исходные данные и результат этих двух примеров противоположны. □
С помощью шестнадцатеричной системы счисления удобно записывать значения байт, так как восемь бит записываются двумя шестнадцатеричными цифрами. Например, число 111100012 запишется как число F116.
4.4. Перевод дробных чисел из одной системы
счисления в другую
Если при переводе конечной дроби в другую систему счисления получается конечная дробь, то такой перевод называется точным. Если при переводе получается бесконечная дробь, тогда перевод называется приближенным.
Правило 4.5. (перевод дробных чисел из n-й в десятичную систему счисления) Вещественное число переводится из n-й в десятичную систему счисления по формуле (4.1).
Правило 4.6. (перевод дробных чисел с нулевой целой частью из десятичной в n-ую систему счисления) Дробное число X, у которого целая часть равна 0, переводится из десятичной в n-ую систему счисления по следующему алгоритму:
1) умножить X на n;
2) получить цифру как целую часть числа X и приписать ее справа от имеющихся цифр;
3) обнулить целую часть числа X;
4) выполнять шаги 1-3, пока X ¹ 0 (при точном переводе) или до получения нужного количества цифр в дробной части (при приближенном переводе с заданной точностью).
Пример 4.6. Перевести число 0,6875 в двоичную систему счисления.
Решение. Вновь схему перевода запишем в виде столбца
(рис. 4.2).
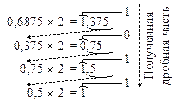
Рис. 4.2. Перевод числа 0,6875 в двоичную систему счисления
На последнем шаге перевода получена единица. После обнуления целой части получим 0. Значит, перевод закончен. Результат перевода числа 0,6875 в двоичную систему счисления – число 0,10112.
Если бы нам было необходимо получить дробную часть с точностью до 3 знаков, то процесс перевода был бы остановлен после получения 3 цифр в дробной части. □
Правило 4.7. (перевод дробных чисел с ненулевой целой частью из десятичной в n-ую систему счисления) При переводе дробных чисел из десятичной в n-ую систему счисления отдельно переводятся целая и дробная части.
Пример 4.7. Перевести число 25,6875 в двоичную систему счисления.
Решение. Перевод целой и дробной частей был выполнен в примерах 4.3 и 4.6. Объединим результаты перевода в одно число:
25,6875 = 11001,10112. □
Десятичная система счисления может использоваться в качестве промежуточного этапа при переводе чисел из одной системы счисления в другую. Приведенные в этой главе правила позволяют перевести числа из одной системы счисления в десятичную, а из нее – в любую другую системы счисления.
Глава 5. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
И СИМВОЛОВ В ПАМЯТИ ЭВМ
Дата добавления: 2019-04-03; просмотров: 727;
