Определение опорных реакций в балках
Простейшими типами опор в балках являются шарнирно-неподвижная опора А и шарнирно-подвижная опора В (рисунок 4.1), а также жесткая заделка (рисунок 4.2). Более сложными типами опор являются упруго-податливые опоры в виде линейных и угловых пружин и распределенного упругого основания.
Могут встретиться три основных типа закрепления балок:
— на двух опорах (однопролетная балка);
— заделка с одного конца (консольная балка);
— составная балка с промежуточным шарниром.
Однопролётная балка (рисунок 4.1)
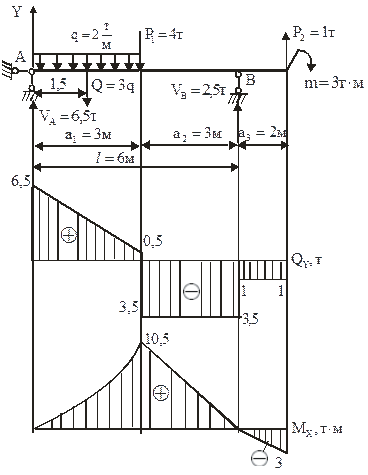
Рисунок 4.1 – Однопролетная балка с консолью, опорные реакции и эпюры внутренних усилий
*Эпюра моментов построена на сжатых волокнах
Дробные величины во всех расчетах необходимо вычислять с 4-мя значащими цифрами с помощью калькулятора во избежание накопления ошибок округления при последующем построении эпюр внутренних усилий.
Порядок определения опорных реакций для однопролетных балок следующий:
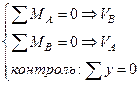 . (4.1)
. (4.1)
Распределённую нагрузку q = 2 т/м на участке длиной 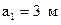 заменяем в статических уравнениях на равнодействующую силу
заменяем в статических уравнениях на равнодействующую силу 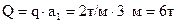 . Далее работаем с этой равнодействующей как с обычной сосредоточенной силой, приложенной в середине участка.
. Далее работаем с этой равнодействующей как с обычной сосредоточенной силой, приложенной в середине участка.
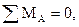
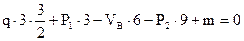 ,
,
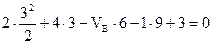 ,
, 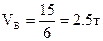 .
.
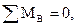
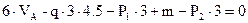 .
.
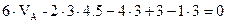 ,
, 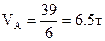 .
.
Контроль: 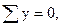
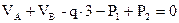 ,
,
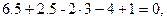
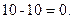
Если расчёты ведутся с 4-мя знаками, то погрешность контроля не превышает 0,1%.
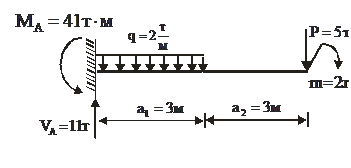
Консольная балка (рисунок 4.2)
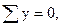 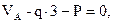
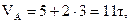
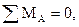 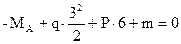
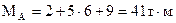 . .
| 
|
| Рисунок 4.2 – Опорные реакции в консольной балке |
Составная двухпролётная балка (рисунок 4.3)
Расчленяем составную балку AD на основную балку АС, имеющую достаточное число опор, и второстепенную балку CD, опирающуюся на основную балку в шарнире С.
Балка CD: 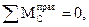
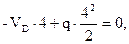
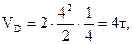
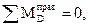
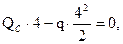
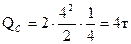 .
.
Контроль: 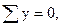
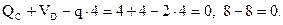
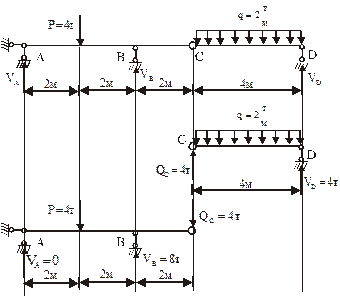
| Рисунок 4.3 – Опорные реакции в составной балке |
Затем внутреннюю реакцию в шарнире переносим на основную балку АС в противоположном направлении, и относим её в разряд внешних сил.
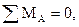
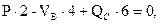
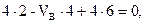
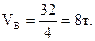
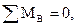
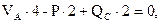
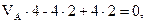
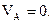
Контроль: 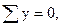
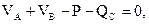
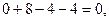
§4.2 Построение эпюр внутренних усилий при изгибе
Внутренние усилия в балках при изгибе также определяют методом сечений, из рассмотрения равновесия отсечённых частей балки (либо левой, либо правой части) – рисунок 4.4.
Сечения проводят на характерных участках, границами которых являются начало или конец балки, места приложения сил и моментов, места расположения опор, начало и конец участка с распределённой нагрузкой.
Правило знаков внутренних усилий (рисунок 4.5):
— поперечная сила 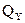 считается положительной
считается положительной 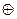 , если она стремится вращать отсечённые части по часовой стрелке.
, если она стремится вращать отсечённые части по часовой стрелке.
— изгибающий момент 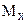 положителен, если он вызывает растяжение нижних и сжатие верхних волокон балки. В этом случае на левую отсечённую часть положительный момент действует против часовой стрелки, на правую отсечённую часть – по часовой стрелке.
положителен, если он вызывает растяжение нижних и сжатие верхних волокон балки. В этом случае на левую отсечённую часть положительный момент действует против часовой стрелки, на правую отсечённую часть – по часовой стрелке.
В соответствии с этим правилом знаков студенты механических специальностей эпюры моментов строят на сжатых волокнах (плюс - вверху), а студенты строительных специальностей – на растянутых волокнах (плюс - внизу).
Внутренние усилия при изгибе наиболее надёжно и просто вычисляются по следующим формулам:
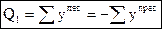 , (4.2)
, (4.2)
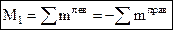 . (4.3)
. (4.3)
Вертикальные нагрузки 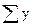 в формуле (4.2) считаются положительными, если они действуют вверх. Моменты внешних сил
в формуле (4.2) считаются положительными, если они действуют вверх. Моменты внешних сил 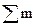 в формуле (4.3) считаются положительными, если они действуют по часовой стрелке относительно центра тяжести сечения.
в формуле (4.3) считаются положительными, если они действуют по часовой стрелке относительно центра тяжести сечения.
Для балки, показанной на рисунке 4.4, составим выражения для внутренних усилий на 1-м участке как через левую, так и через правую части:
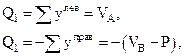
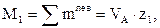
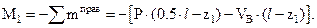
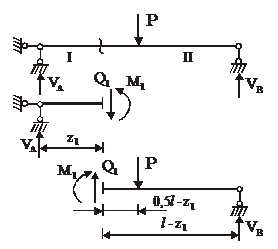
|
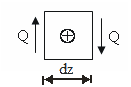 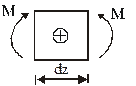 Рисунок 4.5 – Правило знаков для поперечных сил и изгибающих моментов в балках
Рисунок 4.5 – Правило знаков для поперечных сил и изгибающих моментов в балках
|
| Рисунок 4.4 – Метод сечений в однопролетной балке и внутренние усилия в сечении z1 – поперечная сила Q1 и изгибающий момент М1 |
Покажем далее порядок построения эпюр 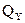 и
и 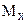 для однопролётной балки, рассмотренной выше, §4.1 (рисунки 4.1, 4.6).
для однопролётной балки, рассмотренной выше, §4.1 (рисунки 4.1, 4.6).
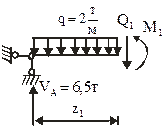 I участок
I участок 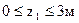
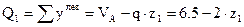 - линейный закон.
- линейный закон.
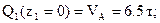
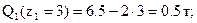
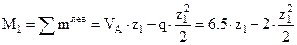 - парабола.
- парабола.
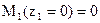 - (шарнир).
- (шарнир). 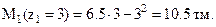
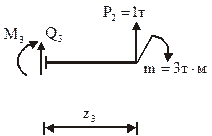
II участок 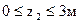
|
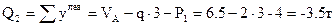
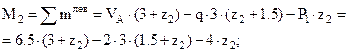
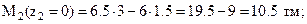
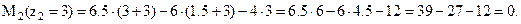
|
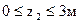 (рассматриваем правую часть).
(рассматриваем правую часть).
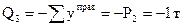 ;
;
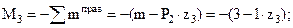
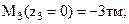
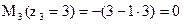 .
.
Эпюры 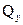 и
и 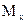 в однопролётной балке показаны выше на рисунке в §4.1 (эпюра моментов построена на сжатых волокнах, как для студентов механических специальностей).
в однопролётной балке показаны выше на рисунке в §4.1 (эпюра моментов построена на сжатых волокнах, как для студентов механических специальностей).
Рисунок 4.6 – Отсеченные части балки для примера на рисунке 4.1 на 3-х участках z1, z2, z3 и соответствующие им внутренние усилия
§4.3 Дифференциальные зависимости Журавского.
Правила контроля построения эпюр
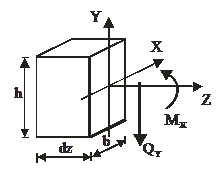
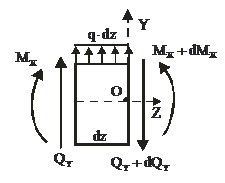
Рассмотрим равновесие бесконечно-малого участка бруса длиной 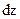 (рисунок 4.7). Учитываем бесконечно-малые приращения усилий dQy и dMx в соседних сечениях.
(рисунок 4.7). Учитываем бесконечно-малые приращения усилий dQy и dMx в соседних сечениях.
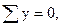
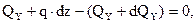
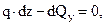
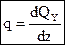 . (4.4)
. (4.4)

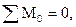
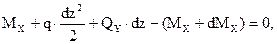
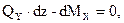
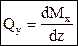 . (4.5)
. (4.5)
Подставляя (4.5) в (4.4), получим (4.6):
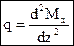 . (4.6)
. (4.6)
Формулы (4.4), (4.5) и (4.6) носят названия соответственно первой, второй и третьей дифференциальных зависимостей Журавского.
| 
|
| Рисунок 4.7 – Равновесие бесконечно-малого участка бруса длиной dz при поперечном изгибе |
Контроль правильности построения эпюр внутренних усилий при изгибе
1. Поперечная сила 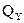 равна тангенсу угла наклона касательной к эпюре
равна тангенсу угла наклона касательной к эпюре 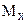 в соответствующей точке.
в соответствующей точке.
2. На участках, где нет равномерно распределённой нагрузки q, эпюра 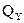 = const ограничена прямыми, параллельными оси z, а эпюра
= const ограничена прямыми, параллельными оси z, а эпюра 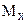 - наклонными прямыми (линейная зависимость).
- наклонными прямыми (линейная зависимость).
3. В сечениях, где поперечная сила равна нулю, изгибающий момент принимает экстремальное значение.
4. На участках, загруженных равномерно распределённой нагрузкой q=const, эпюра 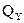 ограничена наклонной прямой (линейная зависимость), а эпюра
ограничена наклонной прямой (линейная зависимость), а эпюра 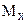 - квадратной параболой.
- квадратной параболой.
5. В сечениях, где приложены сосредоточенные силы (в том числе и реакции) на эпюре 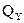 имеется скачок на величину этой силы, а на эпюре
имеется скачок на величину этой силы, а на эпюре 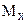 - излом смежных участков.
- излом смежных участков.
6. В сечениях, где приложен сосредоточенный момент m, на эпюре 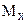 возникает скачок на величину этого момента, на эпюре
возникает скачок на величину этого момента, на эпюре 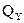 не отражается.
не отражается.
7. Ордината эпюры 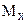 в любом сечении равна части площади эпюры
в любом сечении равна части площади эпюры 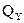 , лежащей по одну сторону сечения, плюс момент сосредоточенной пары (если она есть на участке).
, лежащей по одну сторону сечения, плюс момент сосредоточенной пары (если она есть на участке).
§4.4 Вывод формулы нормальных напряжений при изгибе.
Условие прочности при изгибе
Рассмотрим деформации элементарного участка балки длиной dz при чистом изгибе (рисунок 4.8):
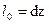 - длина нейтрального волокна;
- длина нейтрального волокна;
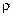 - радиус кривизны нейтрального волокна;
- радиус кривизны нейтрального волокна;
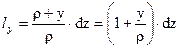 - длина волокна с текущей координатой “y” по высоте сечения.
- длина волокна с текущей координатой “y” по высоте сечения.
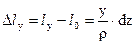 - удлинение волокна
- удлинение волокна 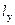 .
.
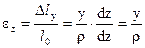 - относительное удлинение волокна
- относительное удлинение волокна 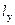 .
.
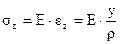 - линейная зависимость по высоте сечения “y” для нормальных напряжений (см. формулу 1.10, рисунок 4.9).
- линейная зависимость по высоте сечения “y” для нормальных напряжений (см. формулу 1.10, рисунок 4.9).
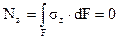 - условие равенства нулю продольной силы.
- условие равенства нулю продольной силы.
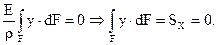
Нейтральная ось проходит через центр тяжести сечения, т.к. статический момент сечения равен нулю.
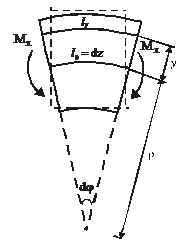
| Рисунок 4.8 – Деформации бесконечно малого участка бруса длиной dz при чистом изгибе в соответствии с гипотезой плоских сечений |
В кривом брусе при R/h < 5÷8 нейтральная ось смещена относительно центра тяжести к центру кривизны; например, для прямоугольника - на величину y0 = h2/12R, для круга - на величину y0 = d2/16R (подробнее смотри учебную литературу).
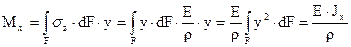 ,
,
где 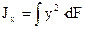 - осевой момент инерции сечения,
- осевой момент инерции сечения, 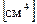 .
.
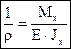 (4.7)
(4.7)
- кривизна изогнутой оси бруса.
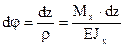 . (4.8)
. (4.8)
С учетом (1.10) формула нормальных напряжений 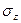 принимает вид:
принимает вид:
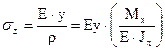 ,
,
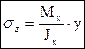 (4.9)
(4.9)
- линейный закон распределения нормальных напряжений по высоте сечения (рисунок 4.9).
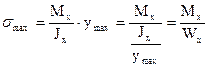 . (4.10)
. (4.10)
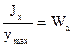 - момент сопротивления сечения,
- момент сопротивления сечения, 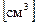 .
.
Условие прочности при изгибе имеет вид:
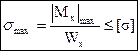 . (4.11)
. (4.11)
Подбор сечений проводят по следующей формуле:
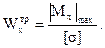 (4.11а)
(4.11а)
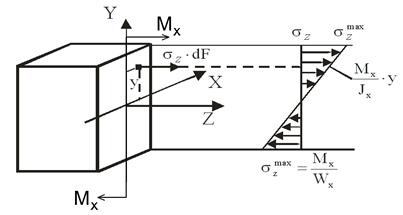
Рисунок 4.9 – Эпюры нормальных напряжений в поперечном сечении балки при изгибе – линейный закон по высоте сечений
Если материал имеет различную прочность на растяжение и сжатие, то составляется два условия прочности - на растяжение для растянутых волокон, на сжатие - для сжатых волокон, причем для несимметричных по высоте сечений моменты сопротивления на растяжение 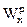 и сжатие
и сжатие 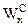 будут разными:
будут разными:
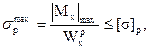 (4.11б)
(4.11б)
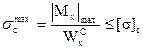 . (4.11в)
. (4.11в)
Рассмотрим далее подбор некоторых типов сечений при изгибе.
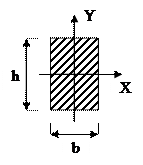 Прямоугольник
Прямоугольник
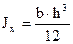 ,
, 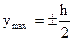 ;
;
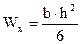 ;
; 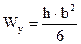 ;
;
Обычно отношение h/b задано коэффициентом k = h/b,
тогда 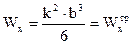 .
.
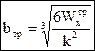 ,
, 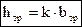 ,
,
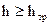 ,
, 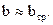 (4.12)
(4.12)
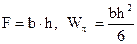 .
.
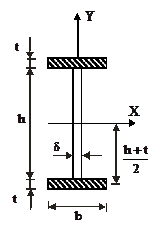
Сварной двутавр (рисунок 4.10)
Точное значение момента инерции вычисляют по формуле:
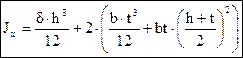 . (4.13)
. (4.13)
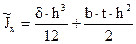 - приближённое значение момента инерции.
- приближённое значение момента инерции.
Точное значение момента сопротивления вычисляют по формуле:
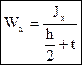 . (4.14)
. (4.14)
Приближённое значение момента сопротивления находят по формуле:
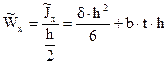 . (4.15)
. (4.15)
Для однопролётной балки в примере, рассмотренном выше в §4.1 - 4.2, 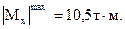
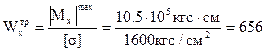 см3.
см3.
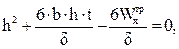
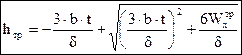 . (4.16)
. (4.16)
| 
|
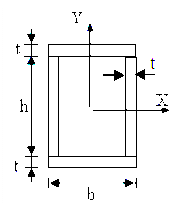
| Рисунок 4.10 – К расчету высоты стенки сварного двутавра и его момента сопротивления | Рисунок 4.11 – К расчету геометрических характеристик сварной коробки |
Пусть b = 20 см, t = 2 см, 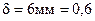 см.
см.
Тогда высота стенки сварного двутавра
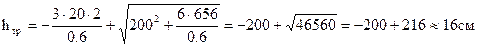 .
.
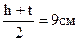 ,
, 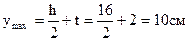 ,
,
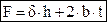 , (4.17)
, (4.17)
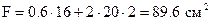 .
.
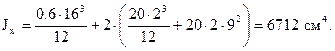
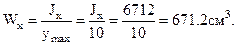
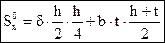 - статический момент половины сечения.
- статический момент половины сечения.
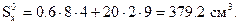
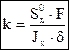 (4.25)
(4.25)
- коэффициент концентрации касательных напряжений по высоте сечения (см. §4.5, Приложение 2).
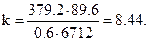
Сварная коробка (рисунок 4.11)
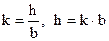 ,
,
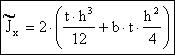 , (4.18)
, (4.18)
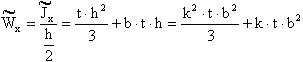
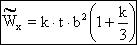 . (4.19)
. (4.19)
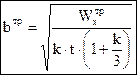 . (4.20)
. (4.20)
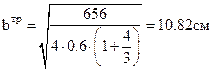
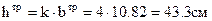 . Принимаем b=11см, h=44см.
. Принимаем b=11см, h=44см.
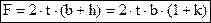 . (4.21)
. (4.21)
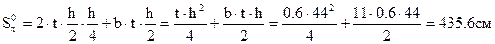 .
.
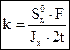 . (4.25)
. (4.25)
k 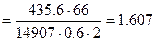 .
.
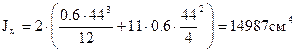 ,
,
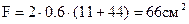 ,
,
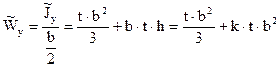 ,
, 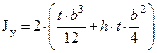 .
.
Треугольник равнобедренный (рисунок 4.12)
Пусть материал имеет различную прочность на растяжение и сжатие, например, чугун, керамика, стекло: [σр] <[σс].
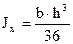 ;
;
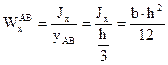 ; (4.22)
; (4.22)
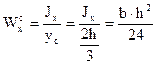 ; (4.22а)
; (4.22а)
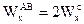 .
.
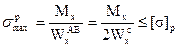 - условие прочности при растяжении.
- условие прочности при растяжении.
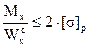
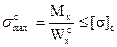 - условие прочности при сжатии.
- условие прочности при сжатии.
|
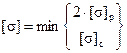 .
.
Рисунок 4.12 – К расчету моментов сопротивления равнобедренного треугольника
Пример 1. Расчёт однопролётной балки на прочность (проектный расчёт)
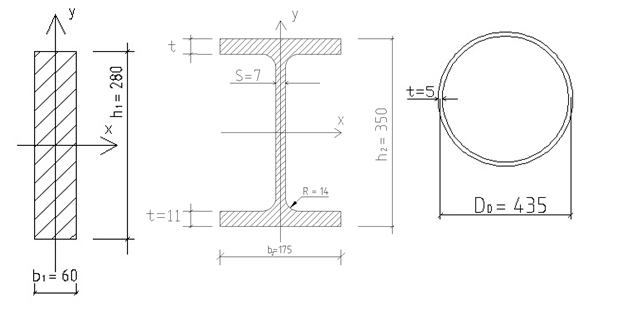
Подобрать сечение стальной балки (рисунок 4.13) в трёх вариантах: прямоугольник (k=h/b=5), прокатный двутавр и тонкостенная труба со стенкой толщиной 5 мм.
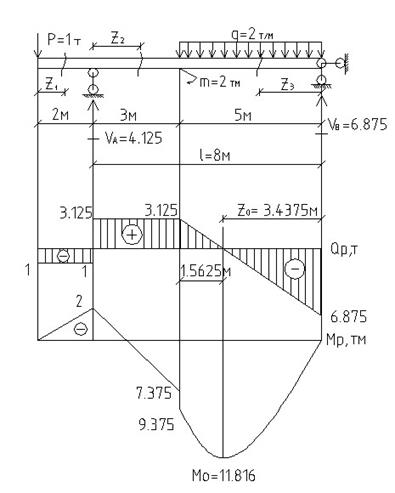
| Рисунок 4.13 - Заданная однопролётная балка и эпюры внутренних усилий |
Решение
1. Расчёт опорных реакций
∑МА=0, -Р·2 + m + q·5· (3 + 2,5) - VB·8 =0
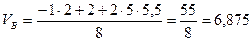 т.
т.
∑MB=0, -P·10 + VA·8 + m - q· 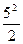 =0,
=0,
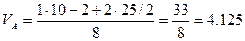 т.
т.
Контроль: 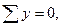
VA + VB – P - q·5=0,
4.125 + 6.875 – 1 - 2·5=0, 11-11=0.
2. Построение эпюр внутренних усилий
 Qy = ∑Yлев = - ∑Yправ, у – вверх,
Qy = ∑Yлев = - ∑Yправ, у – вверх,
 Мх = ∑mлев = -∑mправ, m – по часовой стрелке.
Мх = ∑mлев = -∑mправ, m – по часовой стрелке.
 Qy – по часовой стрелке;
Qy – по часовой стрелке;
 Мх – растягивает нижние волокна. Эпюру моментов студенты строительных специальностей строят на растянутых волокнах, т.е. плюс откладывать внизу.
Мх – растягивает нижние волокна. Эпюру моментов студенты строительных специальностей строят на растянутых волокнах, т.е. плюс откладывать внизу.
а)
|  б) б)
|  в) в)
| |||
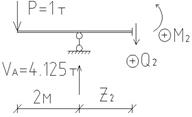
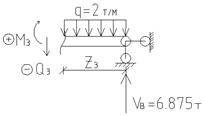
| Рисунок 4.14 – Равновесие отсечённых частей балки для трёх участков: а) 1-й участок; б) 2-й участок; в) 3-й участок (правая часть) |
1 участок, 0 ≤ Z1 ≤ 2м, (рисунок 4.14 а):
Q1 = ∑ Y1лев = - P = - 1т = const. M1=∑mлев = - P·Z1;
M1(0)=0, M1(Z1=2)= - 1·2 = - 2тм (откладывать вверх).
2 участок, 0≤Z2≤3, (рисунок 4.14 б):
Q2= ∑ Y2лев = VA – P = 4.125 – 1 = 3.125т =const.
M2= ∑m2лев = VA·Z2 – P · (2 + Z2) = 4.125· Z2 - 1· (2+Z2);
M2(0) = - 1·2 = - 2тм (откладывать вверх);
М2(3) = 4.125·3 - 1· (2+3) = 7.375тм (откладывать вниз).
3 участок, 0≤Z3≤5, рассматриваем участок справа (рисунок 4.14 в):
Q3= - ∑Y3прав = - (VB - q·Z3) = - (6.875 - 2·Z3);
Q3(0) = -VB = -6.875т (справа участка, опора B);
Q3(5)= - (6.875 - 2· 5) = 3.125т (слева участка).
Определяем координату Z0 нулевой точки на эпюре поперечных сил:
Q3(Z0)= - (6.875 - 2·Z0)=0,
Z0 = 6.875 / 2=3.4375 м.
M3= - ∑m3прав = - (q·Z32 / 2 – VB · Z3 ) = - (2·Z32 / 2 – 6.875·Z3);
M3(0) = 0 (справа участка, опора В);
М3(5)= - (52 - 6.875 · 5) = 9.375тм (слева участка);
Определим скачок на эпюре моментов на границах 2-го и 3-го участков:
ΔM = 9.375 - 7.375= 2тм = m.
Определим экстремум M0(Z0) на эпюре моментов в сечение z0.
M0(Z0)= -(2·Z02 /2 -6.875·Z0) = -(3.43752 - 6.875·3.4375) =11.816тм =Mpmax.
3. Проектный расчёт на прочность
Условие прочности при изгибе составляем для опасного сечения с максимальным по модулю изгибающим моментом.
Опасное сечение – Z0, M0(Z0)= Mpmax = 11.816 тм.
Материал – Сталь Ст3, Rу≈ σт = 2400 кгс/см2, коэффициент запаса n=1,5.
Допускаемое нормальное напряжение при изгибе [σ] равно:
[σ]=σт/n=2400/1.5=1600кгс/см2.
Условие прочности при изгибе имеет вид:
σmax=Mpmax/Wx≤[σ].
Из условия прочности находим требуемый момент сопротивления:
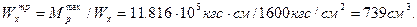
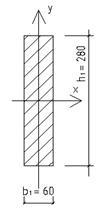
а) Подбор прямоугольного сечения при k = h / b = 5 .
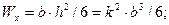
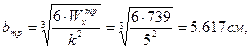
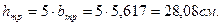
Принимаем после округления следующие размеры сечения (рисунок 15а):
b=6см, h=28см, F1=6·28=168 cм2.
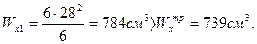
Находим действительные напряжения при изгибе:
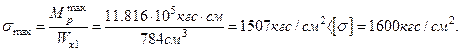
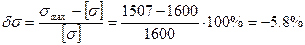 (недонапряжение).
(недонапряжение).
Находим массу балки прямоугольного сечения при длине 10м:
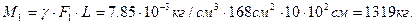
а) б) в)
| |||
| Рисунок 4.15 – эскизы поперечных сечений стальной балки под расчётный изгибающий момент Mmax = 11.816 тм в трёх вариантах: а) прямоугольник; б) прокатный двутавр; в) тонкостенная труба |
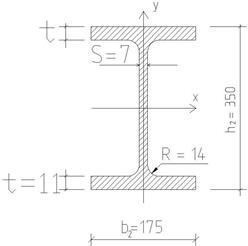
б) Подбор прокатного двутавра серии Б с параллельными полками по СТО АСЧ 20-93 (рисунок 4.15б).
Принимаем по сортаменту ближайший двутавр с большим моментом сопротивления I№ 35Б2, 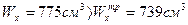 ;
;
b2=175, h2= 350, s= 7мм, t=11мм, F2=63.14см2, m=49,6 кг/м.
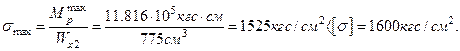
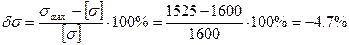 (недонапряжение).
(недонапряжение).
Рассчитаем стоимость металла прокатного двутавра, если m= 49.6 кг/м, с=20 руб/кг, 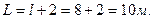
M = m · L =49.6кг/м ·10м = 496кг, С =М ·с= 496 кг · 20руб/кг = 9920 руб.
Таблица 4.2 - Сравнительная таблица поперечных сечений, стальной балки
под расчётный изгибающий момент 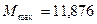 тм
тм
| Параметр | Эскиз сечения | ||
 I№ 35Б2 I№ 35Б2
| 
| 
| |
| F, см2 | 63,14 | 68,32 | |
| Wx, см3 | |||
| M, кг | |||
| Fi/Fl | 1,08 | 2,66 | |
| δσ, % | -4,7 | 0,5 | -5,8 |
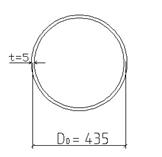
в) Подбор сечения из тонкостенной трубы при толщине стенки t = 5 мм (рисунок 4.15в).
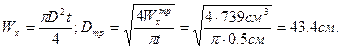
Принимаем D0=435мм – средний диаметр,
D= D0 + t = 435 + 5 = 440 мм – наружный диаметр,
d= D0 – t = 435 – 5 = 430 мм – внутренний диаметр.
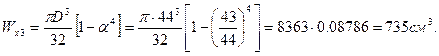
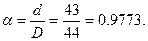
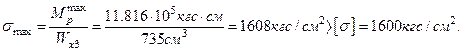
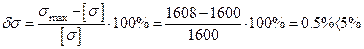 (перенапряжение допустимо).
(перенапряжение допустимо).
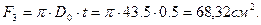
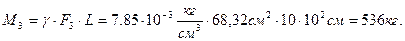
Пример 2. Расчёт плоской железобетонной рамы на прочность
(проектный расчёт)
Рассчитать на прочность железобетонную раму прямоугольного сечения (рисунок 4.16), если k = h/b = 4,5 , расчётное сопротивление железобетона R = 450 кг/см2, стоимость конструкции в деле с = 15000 руб/м3.
 | |||||
 | |||||
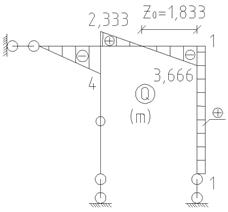 | |||||
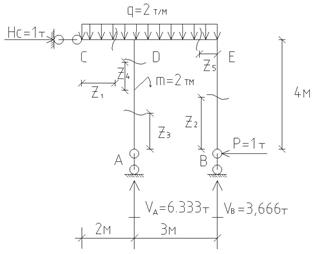
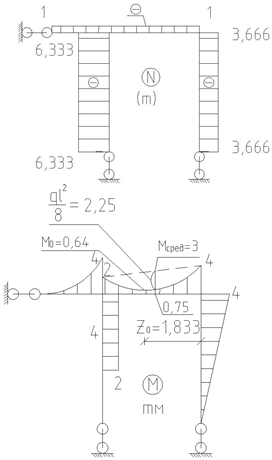
| Рисунок 4.16 – Заданная плоская рама и эпюры внутренних усилий в раме : продольных сил N, поперечных сил Qy и изгибающих моментов Mx |
Решение
Определим опорные реакции, при этом уравнения равновесия составляются так, чтобы в одно уравнение входила только одна реакция:
∑x=0, Hc - P=0, Hc = P = 1т.
∑mD = 0, 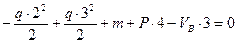
VB = 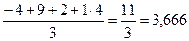 т.
т.
∑mЕ = 0, 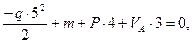
VA = 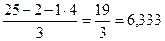 т.
т.
Контроль реакций: ∑y = 0,
VA+ VB – q ∙ 5 = 0, 6,333 + 3,666 – 2 ∙ 5 = 9,999 – 10 = 0,001.
Построение эпюр внутренних усилий выполняем методом сечений по 5-ти участкам (рисунок 4.16, 4.17).
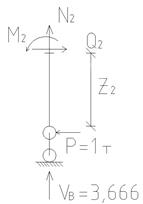 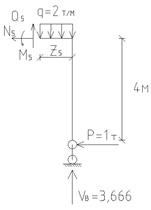 а) а)
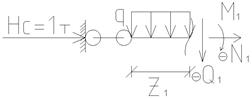 б) д)
в) г) б) д)
в) г)
| ||||||||||
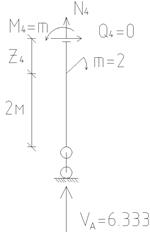
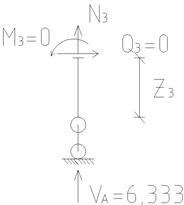
| Рисунок 4.17 – Равновесие отсечённых частей рамы для 5-ти участков: а) 1-й участок; б) 2-й участок; в) 3-й участок; г) 4-й участок; д) 5-й участок |
1 участок, консоль (рисунок 4.17а), 0 ≤ z1 ≤ 2 м.
∑y1 = 0, Q1 = - q ∙z1; Q1(0)=0;
Q1(2) = - 2∙ 2 = - 4т (против часовой).
∑x1=0, N1 = - Нс = - 1т (сжатие).
∑m1 = 0, M1 = q∙ 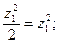
M1(0) = 0, M1(2) = 4тм (растянуты верхние волокна).
2 участок, правая стойка (рисунок 4.17б), 0 ≤ z2 ≤ 4м.
∑y2 = 0, N2=-VB = - 3,666т (сжатие).
∑x2=0, Q2 = P = 1т (по часовой).
∑m2 = 0, M2 = P ∙ Z2 (растянуты наружние волокна);
M2(0) = 0, M2(4) = 1 ∙ 4 = 4тм.
3 участок, 0 ≤ z3 ≤ 2 м (низ левой стойки), (рисунок 4.17 в).
∑x3=0, Q3 = 0.
∑y3 = 0, N3 = - VA = - 6,333т (сжатие).
∑m3 = 0, M3 = 0.
4 участок, верх левой стойки (рисунок 4.17г), 0 ≤ z4 ≤ 2м .
∑y4 = 0, N4 = - VA= - 6,333т (сжатие).
∑x4 = 0, Q4 = 0.
∑m4 = 0, M4 = m = 2тм (растянуты правые волокна).
5 участок, ригель (рисунок 4.17д), 0 ≤ z5 ≤ 3м, рассматриваем ригель справа и правую стойку.
∑x5 = 0, N5= - P = - 1т (сжатие).
∑y5 = 0, Q5 + VB – q ∙ z5 =0,
Q5 = q ∙ z5 - VB = 2 ∙ z5 - 3,666;
Q5(0) = - VB = - 3,666т; Q5(3) = 2 ∙ 3 - 3,666 = 2,333т.
Q5 (z0) = 0, 2 ∙ z0 - 3,666 = 0, z0 = 3,666 / 2 = 1,833м.
∑m5=0, М5 = Р ∙ 4 + q ∙ z52 / 2 - VB ∙ z5 = 1 ∙ 4 + z52 – 3,666 · z5;
M5 (0) = 4тм (справа участка, сечение Е, растянуты верхние волокна).
М5 (3) = 1 ∙ 4 + 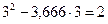 тм (слева участка, сечение D прав).
тм (слева участка, сечение D прав).
М0 (z0 = 1,833м) = 4 + 1,8332 – 3,666 ∙ 1,833 = 0,64 тм (растянуты верхние волокна).
б)
h = 280
b = 70
b1=60
| |||
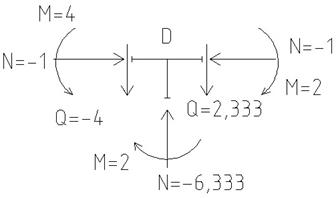
| Рисунок 4.18 - а) Эскиз поперечного сечения железобетонной рамы; б) равновесие узла D; в) равновесие узла E |
Выбираем опасное сечение по максимальному изгибающему моменту и большей по модулю продольной силе – это сечение Е (верх правой стойки):
Mmax= 4тм, |N|max=3,666т.
Рассчитаем требуемый момент сопротивления сечения (материал - железобетон) из условия прочности при изгибе:
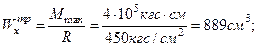
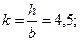
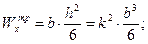
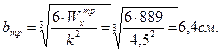
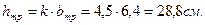
Округляем размеры прямоугольного сечения: один размер - в большую сторону, а другой размер – в меньшую.
Принимаем b=7см, h=28см (рисунок 4.18а).
Вычисляем фактическую площадь и фактический момент сопротивления сечения:
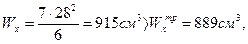
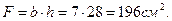
Выполним проверочный расчёт опасного сечения на прочность по максимальным нормальным напряжениям с учётом продольной силы.
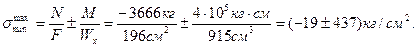
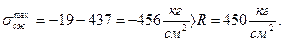
Перенапряжение 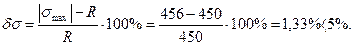
Прочность сечения обеспечена.
Рассчитаем объём материала на все стержни рамы, если сечение всех участков – постоянное, 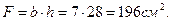
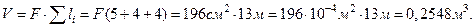
Стоимость всей конструкции:
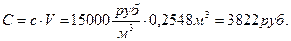
Выполним проверку равновесия узлов рамы по усилиям в стержнях из эпюр. Проверка равновесия узла D (рисунок 4.18-б):
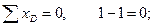
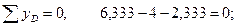

Проверка равновесия узла E (рисунок 4.18-в):
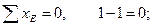
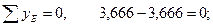
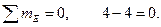
§4.5 Вывод формулы касательных напряжений
при поперечном изгибе (формулы Журавского)
Вычислить касательные напряжения в поперечном сечении бруса 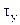 проще всего через парные им продольные касательные напряжения
проще всего через парные им продольные касательные напряжения 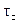 в продольной плоскости, проведённой на высоте y* от центра тяжести сечения (рисунки 4.19, 4.20).
в продольной плоскости, проведённой на высоте y* от центра тяжести сечения (рисунки 4.19, 4.20).
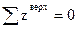 ,
,
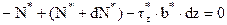 ,
,
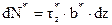 ,
, 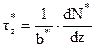 ,
,
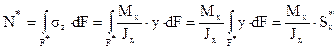 .
.
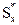 - статический момент верхней части площади поперечного сечения.
- статический момент верхней части площади поперечного сечения.
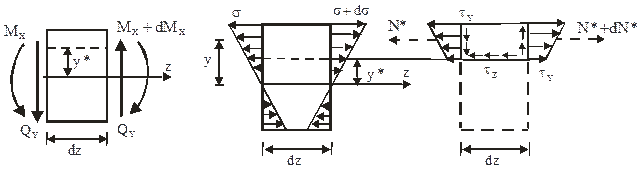
Рисунок 4.19 – Равновесие элементарного участка балки длиной dz под действием нормальных и касательных напряжений при поперечном изгибе
 а) а)
|
 б)
б)
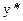 - высота текущего продольного сечения относительно оси z, - высота текущего продольного сечения относительно оси z,
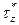 - касательные напряжения в продольном сечении на расстоянии - касательные напряжения в продольном сечении на расстоянии 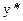 от оси z, от оси z,
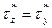 - по закону парности касательных напряжений, - по закону парности касательных напряжений,
|
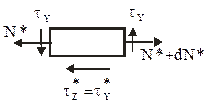
| 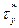 - касательные напряжения в поперечном сечении на расстоянии - касательные напряжения в поперечном сечении на расстоянии 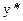 от оси x, от оси x,
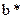 - ширина сечения на расстоянии - ширина сечения на расстоянии 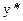 от оси x,
y - текущая координата точек верхней части сечения. от оси x,
y - текущая координата точек верхней части сечения.
|
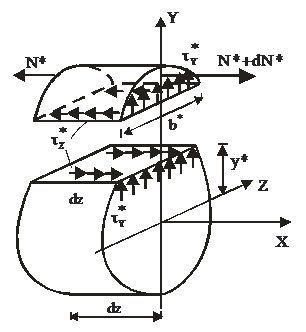
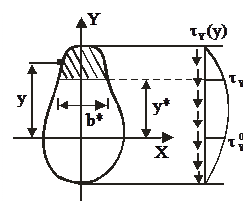
Рисунок 4.20 – а) Равновесие верхней части элементарного участка балки длиной dz при поперечном изгибе; б) эпюра перерезывающих касательных напряжений τy в поперечном сечении по высоте сечения и скалывающих касательных напряжений τz в продольном сечении балки
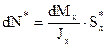 ;
; 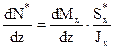 ;
;
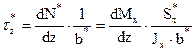 ;
;
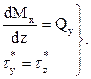
Формула касательных напряжений Журавского “ТУРКСИБ” принимает вид:
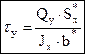 . (4.23)
. (4.23)
Средние перерезывающие касательные напряжения по сечению находим по формуле:
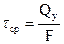 . (4.24)
. (4.24)
Коэффициент концентрации касательных напряжений по высоте сечения находим по формуле:
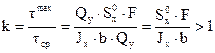 , (4.25)
, (4.25)
где 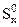 - статический момент половины сечения.
- статический момент половины сечения.
Анализ формулы Журавского
1. Максимальные касательные напряжения возникают на нейтральной оси x (но бывают исключения для некоторых типов сечений).
2. Чем меньше ширина сечения 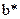 в рассматриваемой точке, тем больше касательное напряжение в этой точке.
в рассматриваемой точке, тем больше касательное напряжение в этой точке.
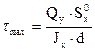 - для стенки двутавра на нейтральной оси (рисунок 4.21),
- для стенки двутавра на нейтральной оси (рисунок 4.21),
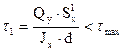 - для стенки двутавра на стыке с полкой,
- для стенки двутавра на стыке с полкой,
где 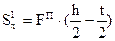 - статический момент полки.
- статический момент полки.
3. Проверка прочности по касательным напряжениям должна выполняться в тех сечениях, где на эпюре 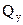 имеется максимальное по модулю значение поперечной силы (обычно возле опор балок).
имеется максимальное по модулю значение поперечной силы (обычно возле опор балок).
| 
|
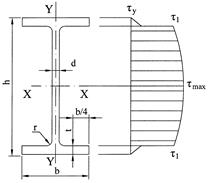
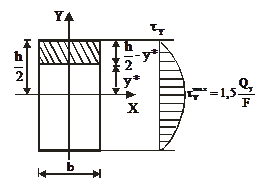
| Рисунок 4.21 – Поперечное сечение прокатного двутавра с параллельными полками и его размерные параметры по ГОСТ 2602083; эпюра касательных напряжений τy | Рисунок 4.22 – Параболическая эпюра касательных напряжений для прямоугольного сечения |
Пример: Построить эпюру касательных напряжений 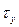 для прямоугольного сечения (рисунок 4.22).
для прямоугольного сечения (рисунок 4.22).
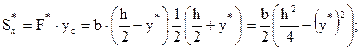
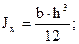
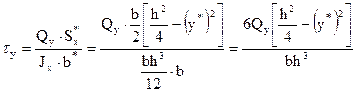 - парабола.
- парабола.
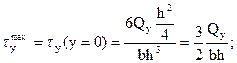
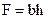 ,
, 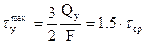 ,
,
где 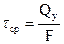 - условные средние перерезывающие касательные напряжения для сечения.
- условные средние перерезывающие касательные напряжения для сечения.
В деревянных балках касательные напряжения могут вызывать скалывание волокон в продольной плоскости, поскольку 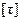 <<
<< 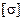 .
.
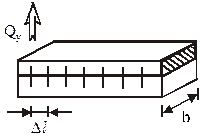
В составных балках (рисунок 4.23) необходимо рассчитывать минимальное количество заклёпок или гвоздей, приходящихся на единицу длины балки (шаг дискретных связей). При этом сила сдвига T, передаваемая на дискретную связь, находится как равнодействующая касательных напряжений 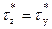 в продольной плоскости стыка в пределах грузовой площади Δl·b* (рисунок 4.23):
в продольной плоскости стыка в пределах грузовой площади Δl·b* (рисунок 4.23):
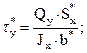
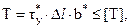
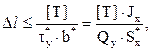 (4.26)
(4.26)
где Δl - шаг сдвиговых связей (обратно пропорционален величине поперечной силы Qy);
[T] - несущая способность заклёпки (гвоздя, нагеля) в соединении на срез.
|
Рисунок 4.23 – Расчетная схема составной балки на дискретных сдвиговых связях (гвозди, шпильки, болты, нагели)
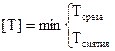 .
.
Если задан шаг 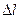 , то подбирают диаметр заклёпок (гвоздей) через требуемую площадь среза
, то подбирают диаметр заклёпок (гвоздей) через требуемую площадь среза 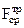 , чтобы обеспечить требуемую прочность соединения.
, чтобы обеспечить требуемую прочность соединения.
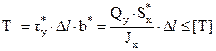 ;
;
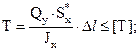 (4.27)
(4.27)
В нормах на проектирование деревянных конструкций формула (4.27) применяется в преобразованном виде после замены Qy·Δl=ΔM, где ΔM – изменение изгибающего момента на участке шага дискретных связей Δl:
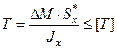 . (4.27а)
. (4.27а)
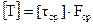 ;
;
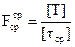 . (4.28)
. (4.28)
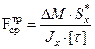 . (4.28а)
. (4.28а)
§4.6 Дифференциальное уравнение изогнутой оси балки
При выводе формулы нормальных напряжений при изгибе мы получили выражение кривизны изогнутой оси балки (4.7):
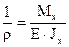 , где
, где 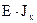 - изгибная жёсткость балки.
- изгибная жёсткость балки.
С другой стороны, из математики известно выражение кривизны любой функции через производную.
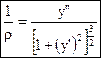 . (4.29)
. (4.29)
Рассматриваем жёсткие балки, когда 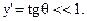
Тогда получаем приближённое дифференциальное уравнение изогнутой оси балки.
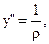 или
или
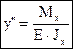 ;
; 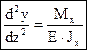 ; (4.30)
; (4.30)
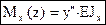 ,
, 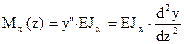 . (4.31)
. (4.31)
С учётом того, что 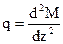 , можно получить после двойного дифференцирования:
, можно получить после двойного дифференцирования:
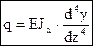 . (4.32)
. (4.32)
Если 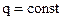 , то
, то 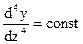 также, и изогнутая ось балки описывается уравнением четвёртого порядка.
также, и изогнутая ось балки описывается уравнением четвёртого порядка.
Если 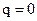 , то
, то 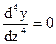 - кубическая функция
- кубическая функция 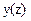 .
.
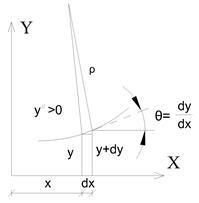
|
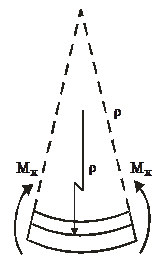
| ||||
| Рисунок 4.24 – а) Математическая кривая у(х) и её кривизна; б) изогнутая ось балки и её кривизна при чистом изгибе |
§4.7 Определение прогибов и углов поворота изогнутой оси
балки методом начальных параметров
Составим выражение для изгибающего момента Мx(z) в произвольном сечении балки z, последовательно добавляем слагаемые при появлении новых нагрузок на участках (рисунок 4.25):
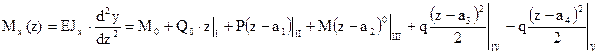 (4.33)
(4.33)
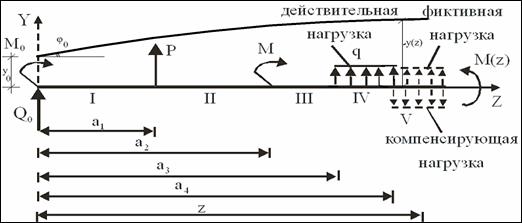
Рисунок 4.25 – Разбиение балки на участки в методе начальных параметров для различных нагрузок
Начальные параметры делятся на 2 группы – статические (М0, Q0) и кинематические (z0, θ0):
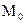 ,
, 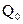 ,
, 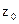 ,
, 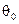 - момент, поперечная сила, прогиб и угол поворота в начале координат.
- момент, поперечная сила, прогиб и угол поворота в начале координат.
Правило знаков
1. Положительные силы и распределенные нагрузки направлены вверх (по оси y).
2. Положительные прогибы отсчитываются вверх (по оси y).
3. Положительные моменты направлены по часовой стрелке.
4. Положительные углы поворота отсчитываются против часовой стрелки.
Для жестких балок, прогибы которых не превышают половину высоты сечения, угол поворота можно приравнять к первой производной от функции прогибов:
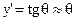 .
.
Выражение для поперечной силы получим интегрированием выражения (4.33) с учетом дифференциальной зависимости Журавского (4.5):
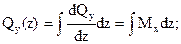
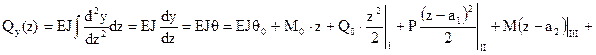
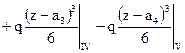 ; (4.34)
; (4.34)
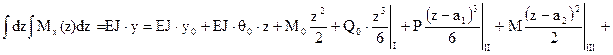
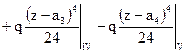 . (4.35)
. (4.35)
Пример 1.
Найти прогиб в середине балки по схеме двухточечного изгиба (рисунок 4.20).
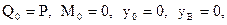
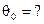
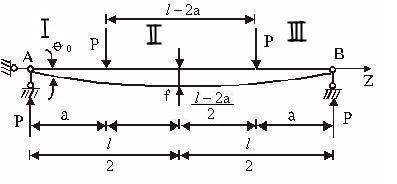
| Рисунок 4.26 – К определению прогибов в балке, нагруженной по схеме двухточечного изгиба, методом начальных параметров |
Найти f - прогиб в середине пролета балки.
I, 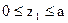 ;
;
II, 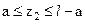 ;
;
III, 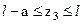 .
.
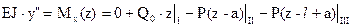 .
.
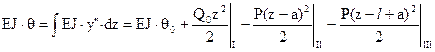 .
.
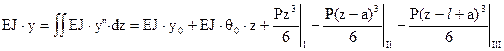 .
.
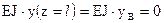 .
.
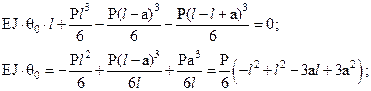
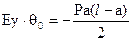 , где
, где 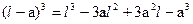 .
.
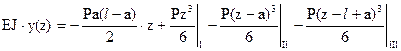 .
.
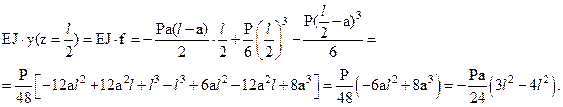
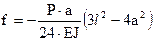 , (4.36)
, (4.36)
где 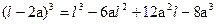 .
.
Если к балке приложены 2 силы 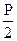 , то прогиб f’=f/2 будет в 2 раза меньше:
, то прогиб f’=f/2 будет в 2 раза меньше: 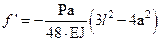 . (4.36а)
. (4.36а)
Пример 2.
Найти прогиб и угол поворота конца
| <== предыдущая лекция | | | следующая лекция ==> |
| ШКОЛА ПОВЕДЕНЧЕСКИХ НАУК | | | Хронологические границы СРЛЯ |
Дата добавления: 2019-04-03; просмотров: 6060;

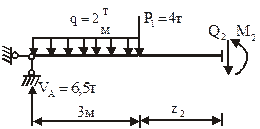

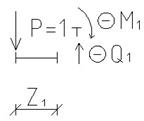
 а)
а)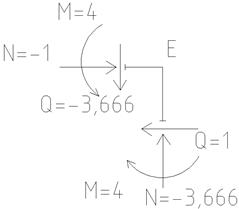 в)
в)