Массовый секундный расход газа

Массовый секундный расход газа может быть найден с помощью уравнения (2), в которое необходимо подставить площадь рассматриваемого поперечного сечения канала и соответствующие ему значения v и W.

Если 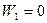, то W подсчитывается по уравнению (14), а удельный объем выражается через его значение в сечении 1-1. Тогда для случая адиабатного течения получим

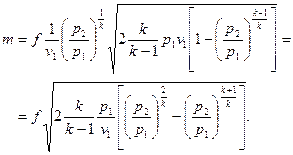(15)

Анализ соплового течения газа через

Суживающееся сопло

Анализ уравнения (15) позволяет перейти к выводу о том, что при заданных 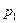, 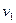и 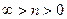(область существования устойчивых равновесных состояний) величина массового секундного расхода зависит от значения выражения, взятого в квадратные скобки. Легко видеть, что при 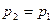(рис. 2) 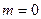. При 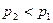расход газа за счет увеличения расширения газа на участке 1-1 2-2 растет. Однако, при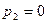 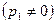m снова становится равным нулю. Поскольку функция (15), будучи непрерывной, дважды проходит через ноль, то должен существовать максимум массового секундного расхода (рис. 3).

Величина соотношения 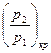, отвечающая 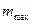найдется, если взять первую производную от выражения в квадратных скобках уравнения (15) и приравнять ее нулю.

В результате получаем, что для адиабатного процесса изменения состояния критический перепад давлений равен

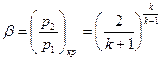. (16)

Естественно, что при подстановке в уравнение (15) вместо 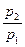критического перепада давлений мы получим максимальную величину массового секундного расхода. Например, для адиабатного течения, которое чаще всего рассматривается в технических приложениях, имеем

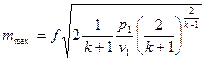. (17)

При дальнейшем уменьшении давления, в окружающей среде 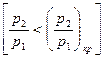расход остается постоянным, равным 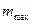. Это явление получило название "кризис течения".

Скорость течения газа при 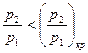также остается постоянной. Эта скорость называется критической скоростью течения 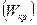. Уравнение для определения 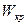может быть получено, если в (14) вместо 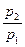ввести критический перепад давлений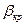

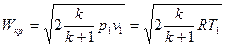. (18)

Разберем физическую картину процесса. По мере движения газа по каналу происходит его расширение, при котором уменьшается 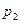и .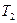

Снижение 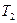приводит к уменьшению местной скорости звука (9), а скорость потока возрастает. В выходном сечении канала скорость звука в соответствии с (9) будет равна

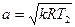. (19)

При кризисе течения скорость потока в выходном сечении определяется (18). Введем в это уравнение вместо 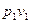температуру Т. Для адиабатного процесса при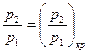

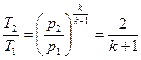
или

.

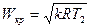Таким образом, при достижении критического перепада давлений на выходе из суживающегося сопла скорость потока достигает местной скорости звука. Между тем, давление распространяется тоже со скоростью звука. В результате, уменьшение в окружающей среде давления ниже 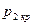не может подойти к устью сопла, и в последнем устанавливается постоянное давление, равное 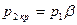(19). Этим объясняется тот факт, что при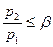

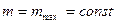
и

.

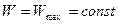Сопло Лаваля

Проведенный анализ касался течения газа через суживающееся сопло. Из него не следует делать вывод о том, что вообще не возможно, например, при адиабатном течении получить скорость потока выше звуковой.

Как следует из уравнения (10.1), для перехода в область сверхзвуковых скоростей необходимо иметь расширяющийся канал. Следовательно, дополняя суживающийса канал, где газ достигает критической скорости, расширяющимся, мы предоставляем газу возможность продолжить свое расширение и приобрести сверхзвуковую скорость. Такое комбинированное сопло называется соплом Лаваля (рис. 4).

Сопло Лаваля целесообразно применять лишь при 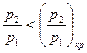. Скорость истечения, например, при адиабатном течении определится с помощью уравнения (14). Расход определится по минимальному сечению, где имеет место кризис течения. Для этого используется уравнение для определения 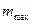, в которое следует подставлять вместо f минимальное сечение сопла f_min.

ЛЕКЦИЯ 7

РЕАЛЬНЫЕ ГАЗЫ

В ряде случаев приходится иметь дело с системами, состояние которых не позволяет использовать модель идеального газа. В качестве примера можно назвать водяной пар в тех состояниях, при которых он используется в паросиловых установках.

Здесь приходится принимать во внимание, что молекулы имеют определенные размеры и между ними существуют силы взаимодействия: притяжение при сравнительно больших расстояниях между молекулами и отталкивание при сближении молекул на малые расстояния.

Модель реального газа представляется в виде твердых шариков диаметром d₀, взаимно притягивающихся друг к другу.

Как видно, модель реального газа отличается от модели идеального газа, во-первых, тем, что сами молекулы имеют некоторый объем, во-вторых, наличием сил межмолекулярного сцепления.

В общем случае, это приводит к тому, что в отличие от идеального газа

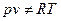
и при T = const

.

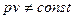Устройство pv – диаграммы реального газа

Впервые подробное экспериментальное исследование зависимости p от v в разных изотермических процессах сжатия реального газа провел на углекислоте в 1857 – 1969 г.г. английский физик Эндрюс. Результаты его экспериментов показаны на рис. 1.

Как видно, при температурах, меньших 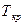, изотермическое сжатие углекислоты (СО₂) вначале сопровождается ростом давления. В точке а начинается процесс конденсации. Состояние, отвечающее этой точке, называют сухим насыщенным паром. При продолжении изотермического сжатия давление остается постоянным, а уменьшение объема сопровождается тем, что все большее количество пара превращается в жидкость.

Наконец, в точке b конденсация завершается, и рабочее тело представляет собой кипящую жидкость. На участке ab одновременно существует и жидкая и газообразная фазы. Состояния, характеризуемые точками на ab, называют влажным насыщенным паром.

Соотношение между паровой и жидкой фазой характеризуют степенью сухости пара - это массовая доля сухого насыщенного пара во влажном. Степень сухости пара определяется выражением

,

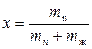где m_n и m_ж – соответственно масса пара и жидкости во влажном насыщенном паре.

Удельный объем сухого насыщенного пара обозначают 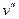(точка а), а кипящей жидкости – 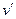(точка b).

Рис. 1. PV – диаграмма реального газа

При продолжении изотермического сжатия в области v < v' отмечается резкое возрастание давления, так как жидкость обладает малой сжимаемостью.

С ростом температуры разность (v" - v'), быстро убывает за счет интенсивного уменьшения v" и некоторого роста v', т.е. с ростом температуры уменьшается разница между плотностями жидкой и газовой фаз.

Уменьшение (v" - v') продолжается вплоть до температуры Т_кр, когда эта разность обращается в нуль (точка К), т.е. в этой точке исчезает различие между плотностями жидкости и пара. Точка К, отвечающая этому состоянию, называется критической точкой. Соответственно давление, температура и удельный объем называются критическими (р_кр, Т_кр, v_кр). Естественно, что все попытки обеспечить путем изотермического сжатия сжижение газа при Т > Т_кр, обречены на неудачу.

Критической температуре можно дать молекулярно-кинетическое толкование. Объединение свободнодвижущихся молекул в каплю, жидкости при сжижении газа происходит исключительно под действием сил взаимного притяжения. Этому препятствует кинетическая энергия движения молекул, равная с среднем kT (k – постоянная Больцмана). Очевидно, объединение молекул в каплю может произойти лишь при том условии, что кинетическая энергия движения молекул, пропорциональная Т, меньше или равна потенциальной энергии из взаимного притяжения (u_o). Если кинетическая энергия больше потенциальной энергии взаимного притяжения, то конденсация жидкости при изотермическом сжатии не сможет произойти. Сопоставление этих положений с результатом анализа диаграммы Эндрюса позволяет сделать вывод о том, что Т_кр – температура, соответствующая равенству указанных энергий

.

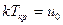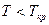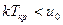Если , то и конденсация при изотермическом сжатии возможна.

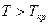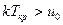Если , то и конденсация при изотермическом сжатии не возможна.