Частные случаи политропного процесса
При рассмотрении политропного процесса предполагалось, что все параметры состояния меняются в ходе процесса, что имеет место обмен энергией между системой и окружающей средой. Вместе с тем, существует группа процессов, при протекании которых накладывается запрет на изменение того или иного параметра состояния, на тот или иной вид энергетического обмена с окружающей средой. Различают четыре вида таких процессов. Это изохорный (v = const), изобарный (р = const), изотермический (T = const) и адиабатный или изоэнтропный (s = const). Рассмотрим эти процессы.
Изохорный процесс
В данном случае запрещается изменение объема (v = const).
Теплоемкость системы
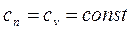 .
.
Определим значение n при v = const. Из (2.19) следует
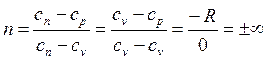
Извлечем корень n-ой степени из (2.22)
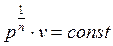
и подставим в него найденное значение показателя политропы. Тогда получим
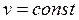 .
.
Таким образом, из общего уравнения политропы получено уравнение изохорного процесса. Последнее позволяет рассматривать изохорный процесс как частный случай политропного процесса при n = 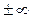 .
.
Определим соотношение между параметрами в изохорном процессе.
Для изохорного процесса имеет смысл искать соотношение лишь между Р и Т, т.к. при v = const отыскание взаимосвязи между Р и v или Т и v лишено смысла.
В общем случае протекания политропного процесса соотношение Р и Т устанавливалось (2.26)
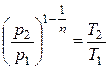 .
.
Если ввести в него n = 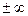 , то
, то
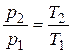 . (2.41)
. (2.41)
Выражение (2.41) известно из физики как закон Шарля.
Изменение внутренней энергии
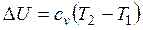 .
.
Изменение энтальпии
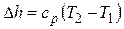 .
.
Изменение энтропии определяется из выражения (2.34)
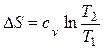 .
.
Работа расширения
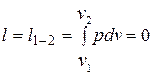 .
.
Из первого закона термодинамики следует
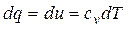
или
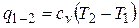 .
.
Изобарный процесс
В данном случае накладывается запрет на изменение давления (p = const).
Теплоемкость системы
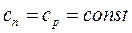 .
.
Определим значение n при р = const. Из (2.19) следует
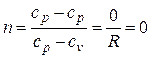 .
.
Если в основное уравнение политропы подставить найденное значение n, то
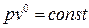 ,
, 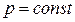 .
.
При рассмотрении изобарного процесса имеет смысл искать соответствие между основными параметрами состояния лишь в виде 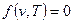 . Уравнение (2.25) при
. Уравнение (2.25) при 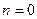 дает
дает
 - закон Гей-Люссака.
- закон Гей-Люссака.
То есть в изобарном процессе изменение объема прямо пропорционально изменению абсолютной температуры.
Изменение внутренней энергии идеального газа не зависит от пути процесса, т.е. U в случае p = const
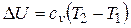 .
.
Изменение энтальпии
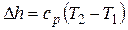 .
.
Изменение энтропии определяется из выражения (2.35)
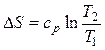 .
.
Работа, производимая газом в ходе изобарного расширения или затрачиваемая на его изобарное сжатие, легко может быть определена по формуле политропного процесса при условии, что 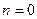 . Это условие сводит все формулы работы политропного процесса к двум:
. Это условие сводит все формулы работы политропного процесса к двум:
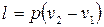 (2.42)
(2.42)
и
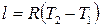 . (2.43)
. (2.43)
Следует отметить, что уравнение (2.42) может быть получено для 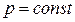 из самого общего выражения работы (2.38) без каких-либо оговорок относительно природы газа. Поэтому данная формула справедлива как для реальных, так и для идеальных газов.
из самого общего выражения работы (2.38) без каких-либо оговорок относительно природы газа. Поэтому данная формула справедлива как для реальных, так и для идеальных газов.
Рассмотрение (2.43) представляет дополнительный интерес в связи с тем, что оно позволяет раскрыть физический смысл газовой постоянной. Действительно, если решить (2.43) относительно газовой постоянной
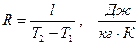 ,
,
то последняя представляется как работа расширения в изобарном процессе 1 кг идеального газа при изменении его температуры на 1 градус.
Тепло, подводимое (отводимое) в ходе изобарного процесса, можно найти с помощью уравнения первого начала термодинамики
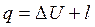
или с помощью теплоемкости:
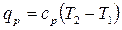 .
.
Дата добавления: 2019-04-03; просмотров: 599;
