Точечные оценки параметров распределения

Будем считать, что измеряемая с. в. 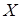имеет неизвестные параметры, которые нам нужно оценить. Например, мы можем знать, что с.в. X~N(a,s²), но параметры aи σ нам неизвестны.

Для того чтобы интуитивно понять смысл дальнейших вычислений, вернемся к набору чисел 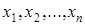, который является реализацией выборки на одном элементарном исходе. Ввиду предположений о том, как проводятся наши измерения, можем сделать вывод, что числа 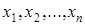появляются равновероятно. Таким образом, можно записать следующий закон распределения:

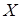
	x1	x2	...	xn
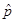
	1/n	1/n	...	1/n

Заметим, что если мы позволим элементарному исходу меняться, то всеперечисленные ниже характеристики станут величинами случайными, поскольку каждая из них будет функцией от n случайных величинX₁,X₂, …,X_n.

Определение 13. Выборочным средним 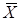(средним арифметическим) наблюдаемых значений с. в. 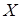называется число, определяемое формулой:

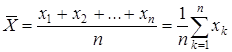
(5)

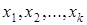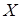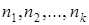Если наблюдаемые данные представлены в виде вариационного ряда, где - варианты значений с.в. , а - соответствующие им частоты, то выборочное среднее вычисляется по формуле

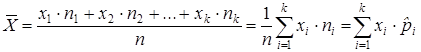
(6)

Определение 14. Выборочной дисперсией 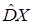значений с.в. 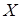называется среднее арифметическое квадратов отклонений наблюдаемых значений этой величины от их выборочного среднего:

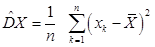
(7)

Аналогично для вариационного ряда выборочная дисперсия определяется формулой:

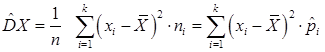
(8)

Интуиция нам подсказывает, что числа 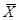и 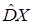должны быть приближениями математического ожидания и дисперсии с.в. 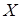. Оказывается, что первая формула ─ это хорошее приближение математического ожидания с.в. 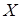, а вторая формула ─ не очень хорошее приближение дисперсии с.в. 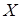. Поэтому вводится следующая исправленная дисперсия:

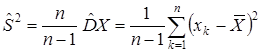
(9)

Данное выражение будет давать хорошее приближение дисперсии с.в. .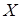

Определение 15. Выборочным средним квадратическим отклонением 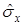называется арифметический квадратный корень из выборочной дисперсии:

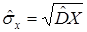
(10)

Определение 16. Пусть закон распределения с.в. 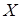содержит неизвестный параметр θ. Оценкой параметра θ называется некоторая функция 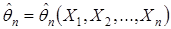отс.в. .

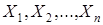Определение 17. Оценка 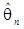называется несмещенной, если .

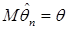Определение 18.Оценка 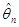называется состоятельной, если для всякого 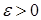выполняется .

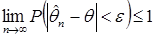В теории вероятности в этом случае говорят, что 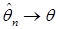(по вероятности).

Определение 19. Оценка 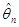называется эффективной, если для любой другой оценки 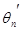параметра θ выполняется соотношение .

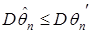Несмещенность оценки означает, что прибор, которым мы производили измерения, либо способ измерения не содержит системной ошибки. В среднем мы получаем измеряемый параметр θ. Состоятельность ошибки говорит о том, что при увеличении числа измерений наша оценка приближается к измеряемому параметру θ. А эффективность означает, что данная оценка имеет наименьший разброс значений.

Теорема 1.Пусть с.в. X~N(a,s²) обладает конечной дисперсией: 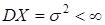. Оценка 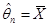, где 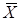– выборочное среднее, является несмещенной и состоятельной оценкой параметра q=a.

□

Теорема 2. Справедливы следующие утверждения:

1) Оценка 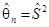параметра q=s², где 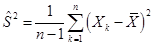, является несмещенной оценкой.

2) Если существует математическое ожидание от 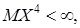то данная оценка состоятельна.

Лемма 1.Пусть 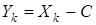, где C— const, 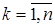. Тогда .

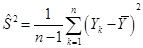Лемма 2.Если 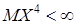, то существует такое числ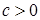о , что .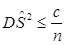

□

Пример 4. Найти несмещенную оценку дисперсии с.в. 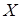на основании данного распределения выборки:

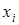
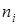
Решение.

Находим выборочную среднюю .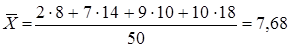

Для вычисления выборочной дисперсии воспользуемся формулой: .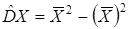

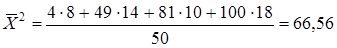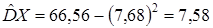, . Находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию): . □

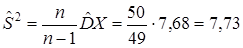Пример 5. Монету подбрасывают 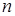раз. Вероятность выпадения герба при каждом подбрасывании равна 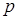. В ходе опыта монета выпала гербом 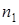раз. Показать несмещенность оценки 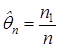вероятности 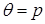выпадения герба в каждом опыте.

Решение. Число успехов 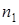имеет биномиальное распределение.

Тогда 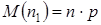, 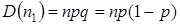. Следовательно,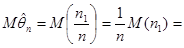 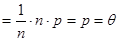, что доказывает несмещенность оценки . □

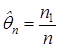Упражнение.Исследовать на несмещённость и состоятельность следующую оценки дисперсии: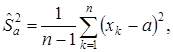

где 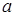– теоретическое значение математического ожидания.

Математическое ожидание и дисперсия являются частными случаями более общих понятий – моментов случайной величины.

Определение 20. Начальным моментом порядка 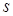с.в. Х называется математическое ожидание 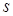- й степени этой величины:

.

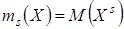(11)

При 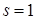получаем математическое ожидание с.в. Х.

Определение 21. Центральным моментом порядка 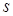с.в. Х называется математическое ожидание величины 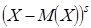, т. е. .

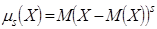При 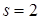получаем дисперсию с. в. Х.

Теорема 3. (Связь между центральными и начальными моментами.) Для всех 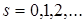справедлива формула .

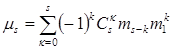Доказательство опускается.

Определение 22. Коэффициентом асимметрии с.в. Х называется число 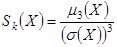. (12)

Коэффициент S_k(X) характеризует асимметрию распределения относительно математического ожидания.

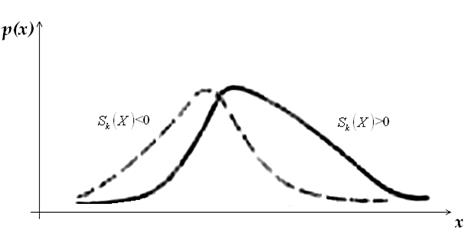
Если плотность распределения с.в. симметрична, то коэффициент асимметрии S_k(X)=0. На рисунке выше приведены графики функций плотности в двух случаях: S_k(X)>0, S_k(X)<0. Если распределение с.в. симметрично, как, например, в случае нормального распределения, то медиана совпадает с математическим ожиданием. Однако для несимметричных распределений математическое ожидание и медиана, вообще говоря, не совпадают.

Определение 23.Коэффициентом эксцессас.в. Х называется число

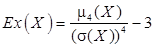_. (13)

Данный коэффициент изучает отклонение от нормальной плотности по части островершинности. При этом “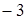” добавлено для того, чтобы для нормального закона распределения 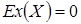. Положительный эксцесс обычно указывает на то, что рассматриваемое распределение имеет более высокую и более острую вершину, чем у соответствующей нормальной кривой, а отрицательный – более низкую и плоскую.

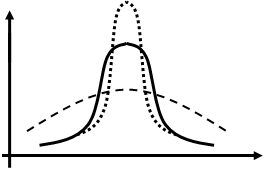
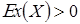
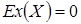(нормальное распределение)

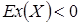
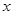
Лекция 3