Исходными уравнениями при доказательстве теоремы являются дифференциальные уравнения движения механической системы.

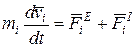(i = 1,2,…, n) (25)

Эта теорема устанавливает зависимость между изменением кинетической энергии механической системы и работой сил.

Для того чтобы появилась элементарная работа необходимо силу умножать на перемещение.

Умножим каждое уравнение системы скалярно на элементарное перемещение 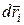(i = 1,2,…, n):

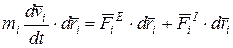(i = 1,2,…, n)

Рассматриваем отдельно выражение

Легко проверить, что

.

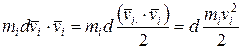Таким образом,

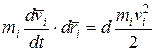
На основании последнего соотношения уравнение принимают вид

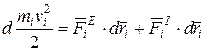(i = 1,2,…, n)

Суммируем эти уравнения, получаем

.

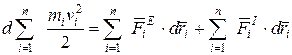Сумма в левой части равенства, представляет собой кинетическую энергию системы, а сумма в правой части - элементарную работу соответственно всех внешних и внутренних сил, то есть

,

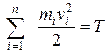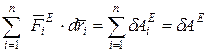
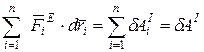
Таким образом,

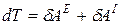. (26)

Формула (26) выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме:

Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, приложенных к точкам системы.

Равенство (26) можно записать в другой форме, удобной для решения задач. Поделим обе части на элементарный промежуток времени dt

.

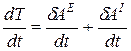Или

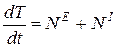, (27)

где

N^E - мощность всех внешних сил;

N^I - мощность всех внутренних сил.