Переходите к изучению п.4.5.

4.5. Средняя квадратическая ошибка арифметической средины.

4.5.1. Арифметическая средина определяется выражением

Х = =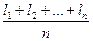

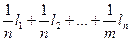
Если оредняя квадратическая ошибка отдельного измерения есть m, а средняя квадратическая ошибка арифметической средины М, то

М² = ,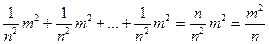

откуда М = ±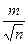

ВОПРОС. Если угол был получен как среднее арифметическое из четырех намерений со средней квадратической ошибкой отдельного измерения ± 4², какова средняя квадратическая ошибка такого угла? (п. 4.5.2).

Ответ 4.5.2. М = ± 2².

Переходите к изучений п. 4.6.

4.6. Выражение средней квадратической ошибки отдельного

измерения через вероятнейшие ошибки

4.6.1. В большинстве случаев точное значение измеряемой величины неизвестно и вместо истинных ошибок мы можем получить лишь уклонение отдельных результатов измерений от арифметический средины. Эти укло­нения называют вероятнейшими ошибками.

Пусть l₁, l₂, . . . l_n - результаты измерения какой-либо величины, точное значение которой l, а арифметическая средина Х.

Тогда истинная ошибка ∆i = l – l_i,,

а вероятнейшая ошибка v_i = X – l_i.

Откуда ∆i - v_i = l – X = δ, где

δ - истинная ошибка арифметической средины, или ∆i = v_i + δ.

Таких равенств можем написать n:

∆₁ = v₁ + δ, ∆₂ = v₂ + δ, … , ∆_n = v_n + δ

Возведем в квадрат эти равенства и сложим:

∆₁² + ∆₂²+…+ ∆_n²= v₁² + v₂²+ … + v_n² + nδ² + 2δ (v₁ + v₂+ … + v_n)

Или [∆² ] = [ v²] + nδ² + 2δ [v], но [v]= 0

тогда[∆² ] = [ v²] + nδ² или .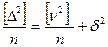

Примем за истинную ошибку арифметической средины

δ = М =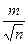

тогда m² = 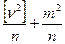или nm² = [ v²] + m²

откуда m = ±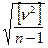

ВОПРОС. Угол намерен четыре раза:

a₁ =58°20¢, a₂ =58°21¢, a₃ =58°21¢, a₄ =58°20¢,

Чему равны средние квадратические ошибки одного измерения н арифметической средины? (п. 4.6.2).

Ответ: m = ± 0¢,6, М = ± 0¢,3.