Переходите к изучению п.3.5.

3.5.Рельеф местности и его изображение на планах и картах.

3.5.1. Различают следующие основные формы рельефа: равнину, гору, котловину, хребет, лощину и седловину.

На современных картах и планах рельеф местности изображается горизонталями. Крутые участки земной поверхности (обрывы, осыпи, ска­лы, курганы, ямы, овраги, промоины и пр.) изображаются специальными условными знаками.

Горизонталь на местности есть след, образованный пересечением горизонтальной плоскости с физической поверхностью Земли (рис.1.12).

Горизонталь на плане есть проекция горизонтали на местности в масштабе плана.

Кратчайшее расстояние между двумя последовательными горизонта­лями на плане называют заложением.

Разность высот двух последовательных горизонталей h называется высотой сечения (рис. 1.12). В зависимости от масштаба характера и назначения плана (карты) высоты сечения принимают равными 1,2, 5, 10 и т.д. метров.

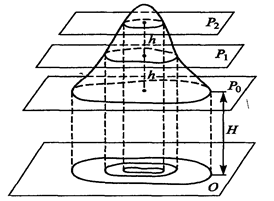
Рис. 1.12. Изображение рельефа горизонталями

Свойства горизонталей:

- все точки лежащие на одной горизонтали, имеют одну высоту;

- все горизонтали должны быть замкнуты в пределах плана или карты или за их пределами;

- горизонтали не могут пересекаться на плане;

- расстояние между горизонталями в плане характеризует крутизну ската.

Самое короткое расстояние между горизонталями соответствует направлению наибольшей крутизны.

Направление ската выраженного горизонталями указывается берг-штрихом.

ВОПРОС. Что называется горизонталью?

1. След от сечения физической поверхности Земли горизонтальной

плоскостью (п. 3.5.2).

2. Кривая, соединяющие точки поверхности Земли имеющие равные высо­ты (п. 3.5.3).

Ответ 3.5.2, 3.5.3. Оба ответа верны.

Переходите к следующему вопросу.

ВОПРОС. Что называется заложением при изображении рельефа горизонталями?

1. Расстояние по высоте между двумя последовательными горизонталями (п. 3.5.4).

2. Кратчайшее расстояние между двумя последовательными горизон­талями в плане (п. 3.5.5).

Ответ 3.5.4. Вы ошиблись, выбрав этот ответ. Расстояние по высоте между двумя последовательными горизонталями называется высотой сечения. Выберите другой ответ.

Ответ 3.5.5. Выбранный Вами ответ верен.

Переходите к изучению п. 3.6.

3.6. Определение по горизонталям отметки точки,

уклона линии, направления скатов, построение профиля

3.6.1. Если точка лежит на горизонтали, то ее отметка устанав-ливает­ся по подписи этой горизонтали. Если точка лежит между горизонталями, то ее отметка устанавли­вается интерполированием между подписями (отметками) горизонталей.

Если линия AВ (рис.1.13) наклонена к горизонту АС под углом, то тангенс этого угла называется уклоном линии и обозначается буквой i.

i = tg a = h / d

т.е. уклон линии равен отношению превышения h к заложению d.

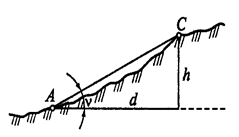
Рис. 1.13. Схема к оп­ределению

положения точки по высоте

Уклон принято выражать в тысячных долях или процентах. Как видно из формулы, уклон тем больший, чем меньше заложение.

Масштаб заложений. Чтобы не прибегать каждый раз к вычислению на плане строят график, называемый масштабом заложений (рис.1.14).

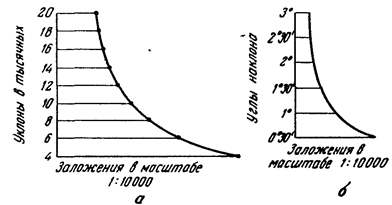
Рис. 1.14. Графики для определения крутизны скатов

Примем в формуле h =2 м и i =0.006, 0.008, 0.01, и т.д. найдем соответствую­щие d. Они будут равны 333, 250, 200 и т.д.

На вертикальной прямой отложим произвольные равные отрезки и подпишем у концов их последовательно 0.006, 0.008, 0.01, и т.д. Через каждую точку проведем горизонтальную прямую и на ней отложим в масш­табе плана соответствующее значение d.. Концы отложенных отрезков соединим кривой. Полученный график и представит масштаб заложений. При помощи этого масштаба определяют уклон линии, взятый по плану между двумя последовательными горизонталями.

Иногда строят масштаб заложений, позволяющий определить крутизну в углах наклона. Для этого при h =2 в предыдущей формуле заложе­ние будет равно d =ctg a.

Из таблиц тригонометрических функций выписывают котангенсы уг­лов 0°30, 1°, 1°30, 2° и т.д., находят заложения, откладывают их на горизонтальных прямых предыдущего чертежа в масштабе плана. Концы отложенных отрезков соединяют непрерывной кривой.

Направление ската определяется берг-штрихами указанных на
горизонталях, кроме того направление ската можно определить по подпи­сям горизонталей - цифры подписей ставиться так, чтобы верх цифр был вверх, а низ цифр - вниз по скату.

Наконец направление оката можно опре­делить по месту расположения гидрографической сети - воды текут в низинах.

ВОПРОС. Для чего строят масштаб заложений?

1. Для определения превышений точек (п. 3.6.2),

2. Для определения уклона линии (п. 3.6.З).

Ответ 3.6.2. Нет. Вы поспешили с ответом. Вернитесь к п.3.6.1 и выберите правильный ответ.

Ответ 3.6.3. Совершенно верно.

Переходите к следующему вопросу.

ВОПРОС. По каким призракам определяется направление ската, выраженно­го в горизонталях?

1. По берг-штрихам (п. 3.6.4)

2. По подписям горизонталей (п. 3.6.5).

3. По месту расположения гидрографической сети (п. 3.6.6).

Ответ 3.6.4., 3.6.5., 3.6.6. Все три признака принимаются во внимание: берг-штрихи ставиться как указатели ската; цифры подписей горизонта­лей ориентируются - верх цифр вверх по скату; а низ цифр - вниз по окату. Воды текут в низинах - это тоже признак для определения ската.

Переходите к изучению п.3.6.7.

3.6.7. Пусть требуется построить профиль линии PL (рис.1.15).

Проводим произвольную прямую PL и на ней откладываем расстояние между точка­ми (p, k, a, b и т.д.) пересечения горизонталей

карты с прямой PL. Высоты этих точек известны и равны высотам соответствующих горизонталей. Откладываем их на перпендикулярах к прямой PL. Соединяя вершины пер­пендикуляров прямыми линиями, получим профиль. Чтобы профиль выражал­ся более рельефно, высоты точек на перпендикулярах откладывают в де­сять раз крупнее, чем масштаб карты.

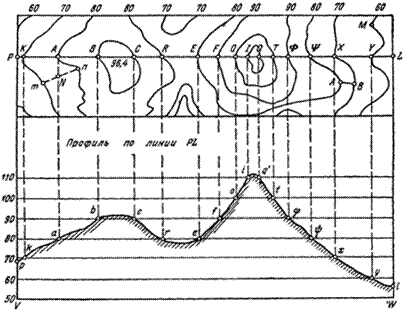
Рис. 1.15. Построение профиля

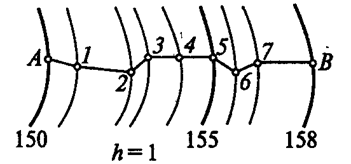
Теперь пусть из точки А (рис.1.16) требуется провести ломаную линию в точку В так, чтобы уклон этих линий нигде не превышал 0.05.

Проще всего задача решается с помощью масштаба заложений для уклонов. Взяв по нему раствором циркуля заложение а_пр соответствующее уклону, засекают последовательно точки 1, 2, … 7 – все горизонтали от точки А до точки В. Соединив все точки, получают линию с заданным уклоном.

Рис 1.16. Проведение на карте линии заданного уклона

ВОПРОС. Почему при построении профиля при помощи горизонталей вертикальный масштаб берут крупнее горизонтального?

1. Для большей точности (п.3.6.8)

2. Для наглядности (п.3.6.9).

Ответ 3.6.8. Точность вертикального построения профиля возрастает, но это не основная причина. Вернитесь к п.3.6.7. и выберите правильный ответ.

Ответ 3.6.9. Совершенно верно. Так как колебания высот точек земной поверхности невелики, то построенный профиль, где масштабы горизонтальный и вертикальный одинаковы, будет ненаглядным. Переходите к изучению п.4.1.

Глава 4. Элементы теории ошибок измерений.

4.1. Свойства случайных ошибок измерений.

4.1.1. Геодезические измерения сопровождаются ошибками: грубыми, сис­тематическими и случайными.

Грубые ошибки являются следствием промаха при производстве изме­рений. Для обнаружения грубых ошибок необходимо производить контроль- ные измерения и после обнаружения исключить их из результатов измерений.

Ошибки систематического характера возникают из-за влияния одно-

сторонних факторов, искажающих результаты измерений, например, от неправильной длины мерной ленты, наличия наклона горизонтальной оси вращения трубы и т.п. Во всех случаях следует стремиться к исключению или ослаблению ошибок систематического характера, введением поправок в результаты измерений.

Случайные ошибки неизбежны при выполнении измерений. Результат измерений по абсолютному значению может быть больше или меньше величины измеряемого объекта. Поэтому ошибка измерений будет иметь знак плюс или минус. При большом числе измерения какой-либо величины эти ошибки подчинены статистической закономерности. Установлено, что случайные ошибки обладают следующими свойствами:

1. Свойство ограниченности, т.е. абсолютные значения результатов измерений не могут быть больше некоторого известного предела, то есть | ∆| ≤ ∆_пред, величина этого предела зависит от условий, в которых производится измерение.

2. Свойство унимодальности, т.е. в данном ряду случайных ошибок малые по абсолютному значению ошибки встречаются чаще больших.

3. Свойство симметричности, т.е. в данном ряду результатов измерений положительные ошибки встречаются также часто, как и равные им по абсолютному значению отрицательные.

4. Свойство компенсации, среднее арифметическое из всех случайных ошибок данного ряда равно точных измерений одной и той же случайной величины при неограниченном возрастании числа измерений стремится к нулю .

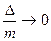4.2. Арифметическая середина

4.2.1. Если имеется ряд результатов равноточных измерений l₁, l₂, . . . l_n одной и той же величины, то за окончательное значение принимают L – среднюю арифметическую величину из всех результатов.

Если Х – истинное значение измеряемой величины, то

∆₁ = l₁ –Х, ∆₂ = l₂ –Х, . . . , ∆_n = l _n –Х..

Сложив правые и левые части уравнения, получим

(∆₁ + ∆₂ +…+ ∆_n) =( l₁ + l₂ +…+l _n) - n Х

Или сокращенно [∆] = [ l ] - n Х, откуда

Х = [ l ]/n - [∆]/n.

Пo по четвертому свойству случайных сшибок с увеличением числа измерений [∆]/n. → 0.

Следовательно Х = [l] / n.

Таким образом, арифметическая средина есть наиболее надежный результат, который принимается за вероятнейшее значение измеряемой ве­личины.

ВОПРОС. Чему будет равно вероятнейшее значение длины линии, если результаты четырех измерений ее равны: 90.12, 90.18, 90.10, 90.12 (п. 4.2 .2)?

Ответ: 90.18

4.2.2. Если вычисленное Вами значение совпадает с ответом, то

переходите к изучению п..4.3. '

4.3. Средняя квадратическая ошибка отдельного

измерения; предельная ошибка.

4.3.1. Если точное значение измеряемой величины есть X, а измеренное l, то ∆ = X - l называют истинной ошибкой измерений.

Для ряда измерений с истинными ошибками ∆₁ + ∆₂ +…+ ∆_n средней квадратической ошибкой одного измерения называют величину

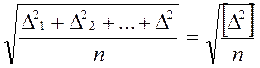
и принимают ее за меру точности измерений.

Предельной ошибкой называют наибольшее значение случайной ошибки, которого она может достичь ври данных условиях измерений. Теоретически доказывается, что она может быть больше средней квадратической в 32 случаях на 100, больше удвоенной средней квадратической только в 5 случаях из 100 и больше утроенной средней квадратической всего лишь в 8 случаях из 1000.

Следовательно, маловероятно, чтобы случайная ошибка измерений получилась больше утроенной средней квадратической. Поэтому утроенную среднюю квадратическую ошибку считают предельной

∆_пред = 3 m.

ВОПРОС. Что принимают за меру точности измерений?

1. Случайниую ошибку (п.4.3.2).

2. Среднюю арифметическую из случайных ошибок (п.4.3.3.).

3. Среднюю квадратическую ошибку (п.4.3.4).

Ответ 4.3.2. Нет. Случайную ошибку не принимают за меру точности. Выберите другой ответ.

Ответ 4.3.3. Нет. Среднюю арифметическую из случайных ошибок не принимают за точности. Выберите другой ответ.

Ответ 4.3.4. Правильно. Чтобы судить о степени точности данного ряда изме­рений, надо вывести среднюю ошибку отдельного измерения. Казалось бы, следовало взять среднее арифметическое из всех случайных ошибок. Од­нако, на величину этого среднего влияли бы разные знаки отдельных ошибок и могло случиться, что ряд с более крупными отдельными ошибками полу­чил бы меньшую среднюю ошибку, нежели ряд с меньшими ошибками. Если же составить среднее из абсолютных значений случайных ошибок, то при этом не будет достаточно отражено наличие в данном ряде отдельных, крупных ошибок, а чем крупнее в данном ряде отдельные ошибки, тем меньше его точность. Исходя из этих соображений установили такой кри­терий для оценки точности измерений, который не зависит от знаков отдельных ошибок и на котором наличие сравнительно крупных отдельных ошибок рельефно отражено. Этим требованиям удовлетворяет средняя квадратичеокая ошибка отдельного измерения.

Переходите к изучению п. 4.4.

4.4. Средняя квадратическая ошибка функций

измеренных величин.

4.4.1. Иногда искомую величину нельзя определить непосредственно, но можно найти ее значение косвенным путем, измерив одну или несколько величин связанных с определяемой величиной функциональной зависимостью.

1.Рассмотрим функциюZ = X + У, где X и У независимые слагаемые. Если случайные ошибки слагаемых DХ и DУ, то

Z + DZ = (X + DХ) +(У + DУ),

Взяв разность, получим: DZ = DХ + DУ.

Если каждое влагаемое было измерено n раз, то мы можем получить ряд соотношений, которые возведя в квадрат, получим

DZi² = DХi ² + DУi² + 2 DХiDУi

Сложив эти равенства и разделив их на n, получим:

DZ² / n = DХ²/n + DУ²/ n + 2 DХDУ/ n ,

но каждое произведение DХDУ обладает свойствами случайных ошибок при большом n последний член в правой части можно отбросить, тогда

DZ² / n = DХ²/n + DУ²/ n или m_z² = m_x² + m_y².

Этот же результат получим и для Z= Х - У

Когда m_x = m_y = m, то m_z = ± m √2.

2. Возьмем функцию Z = Х₁ ± Х₂ ±……±Х_п многих независимых величин. Пусть m_z, m₁, m₂, …, m_n средние квадратические ошибки функции и аргументов. Тогда

m_z² = m₁² + m₂² +…+ m_n².

В частном случае, когда все аргументы имеют одну и ту же среднюю квадратическую ошибку m предыдущая формула примет вид

m_z = ± m√ n.

3. Возьмем функцию Z = КХ (К-постоянное число), для которой соотношение между случайными ошибками, будет

DZ = К DХ.

Если было n измерений величины Х, то будем иметь n уравнений. Возводя в квадрат каждое из них, получим n равенств вида

DZi² = К² DХi².

Сложив все уравнения и разделив на n, найдем [DZ²]/n.= К² [DХ²]/n

или m_z² = К² m_х² откуда m_z = К m_х

4. Пусть дана функция Z = К₁ Х₁ ± К₂ Х₂ ± … ±К_n.Х _n.

Положим Z₁ = К₁ Х₁ ; Z₂ = К₂ Х₂; … Z _n = К_n Х_n,

тогда m_z1 = К₁ m₁, m_z2 = К₂ m₂, …, m_{z n} = К_n m_n.

Теперь функция примет вид

Z = Z ₁ ± Z ₂ ± … ± Z _n.

для этой функции будем иметь

m_z² = m_z1² + m_z2² + m_zn².

Подставляя сюда значения m_zi получим:

m_z² = (К₁ m₁)² + (К₂ m₂)² +…+(К_nm _n)².

5. Рассмотрим теперь функцию самого общего вида от многих неза­висимых величин

Z = f (X₁ , X₂ , . . . Х_n )

Если DХi - случайные ошибки аргументов, то

Z +DZ = f (X₁ + DХ₁, X₂ + DХ₂, . . . X_n + DХ_n )

Разлагая функцию в ряд Тейлора, получим

Z +DZ = f (X₁ , X₂ , . . . Х_n ) +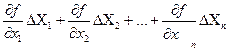

Откуда DZ =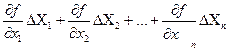

или обозначая 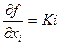получим DZ = К₁DХ₁ + К₂ DХ₂,+ . . . +К_n DХ_n.

Это выражение общего вида, следовательно

m_z² =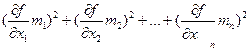

ВОПРОС. Чему рана ошибка в длине окружности, если радиус ее R = 100,00 м измерен в ошибкой m = 0,051 м? (п. 4.4.2)

Ответ 4.4.2. m = 0,320 м.

ВОПРОС. Чему равна ошибка суммы двух линий, измеренных с ошибками.

S₁ = 210,00 м ± 8,9 cм

S₂ =180,00 м ± 8,1 см ? (п. 4.4.3).

Ответ 4.4.3. S = 390.00 ±12 см

ВОПРОС. Чему рана ошибка площади треугольника, если основание в = 112,00 м измерено со средней квадратической ошибкой m_в = ± 5 см и высота с ошибкой m_h ± 3 см. Площадь треугольника р =3370,08 м2 (п. 4.4.4).:

Ответ 4.4.4. m_р = 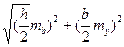= ± 2.25 м.