Контрольные задания по главам 2 страница
Так как распределение величин нормальное, воспользуемся методом Фостера-Стюарта [21], дающим наиболее надежный практический результат. Он более чувствителен к выявлению тренда, чем классическая проверка гипотезы о случайном характере расхождения средних.
По исследуемому динамическому ряду валового сбора зерна с 1955-2006 гг. (табл.1) последовательным сравнением уровней определим характеристики 5 (для обнаружения тенденций в изменении дисперсии) и d (для обнаружения тенденций в средней):
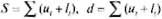
где u и l - вспомогательные переменные.
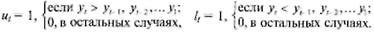
y - фактические значения ряда динамики.
В рассматриваемом случае 5= 13, d = 7. Показатели S и d асимптотически нормальны и имеют независимые распределения. Они существенно зависят от порядка расположения уровней во времени. С учетом их фактических значений, применяя t-критерий Стьюдента, проверяется гипотеза о том, можно ли считать случайными разности d -0 и S - 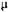 , т. е.:
, т. е.:
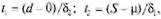
где 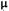 - математическое ожидание величины S, определенное для случайного расположения уровней во времени;
- математическое ожидание величины S, определенное для случайного расположения уровней во времени;
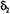 - средняя квадратическая ошибка величины d;
- средняя квадратическая ошибка величины d;
 - средняя квадратическая ошибка величины S.
- средняя квадратическая ошибка величины S.
Необходимые для получения t-критерия показатели 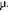 ,
, 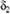 ,
, 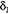 табулированы, например, в [4] и при числе уровней ряда, равном 50, составляют:
табулированы, например, в [4] и при числе уровней ряда, равном 50, составляют: 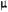 = 6,99;
= 6,99; 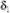 =2,12;
=2,12; 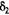 = 2,64. Проверка d дает t1= 2,65, при проверке S получаем t2 = 2,83. Поскольку оба результата выше табличного значения
= 2,64. Проверка d дает t1= 2,65, при проверке S получаем t2 = 2,83. Поскольку оба результата выше табличного значения 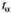 = 2,42 критерия Стьюдента при уровне значимости
= 2,42 критерия Стьюдента при уровне значимости  = 0,01, гипотеза о существовании тренда подтверждается, и можно прогнозировать валовой сбор зерна на ближайшие 3-5 лет методом экстраполяции тренда.
= 0,01, гипотеза о существовании тренда подтверждается, и можно прогнозировать валовой сбор зерна на ближайшие 3-5 лет методом экстраполяции тренда.
Выделение тренда может быть произведено тремя методами: скользящей средней, укрупнения интервала или аналитического выравнивания. Пол аналитическим выравниванием, которым мы и воспользовались, подразумевается определение основной проявляющейся во времени тенденцией развития изучаемого явления. Для этого находят некую функцию от времени f(t), которая наилучшим образом соответствует общей тенденции и дает содержательное объяснение рассматриваемому процессу. Выбор вида функции является достаточно сложным процессом и обычно несет в себе большую долю субъективизма.
Использование пакетов прикладных программ, например Statistica, MS EXEL и др.. позволяет проводить многовариантные расчеты по элементарным и комбинированным аппроксимирующим функциям и выбирать наиболее адекватную из них. Выбранная прогнозная эмпирическая функция, описывающая динамический ряд. должна отвечать необходимым и достаточным условиям. Эта аппроксимирующая функция должна минимизировать стандартное отклонение S на интервале оценивания, обеспечивать тесноту связи (по коэффициенту корреляции); аппроксимирующее уравнение должно быть адекватно фактической временной тенденции валового сбора (по F-критерию) и устранять автокорреляцию.
Динамика валового сбора довольно сложна и циклична в зависимости от периода развития сельскохозяйственного производства, уровня НТП, изменения природно-климатическим условий в соответствии 5-летним циклом колебания урожайности и 11-летним циклом солнечной активности и др. факторов. Поэтому для аппроксимации динамического ряда валового сбора, кроме линейных и параболических зависимостей, применены и некоторые виды комбинированных функций. Параметры уравнений трендов рассчитаны методом наименьших квадратов (см. рис. 1-6):
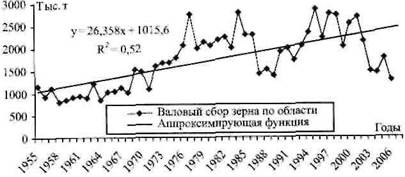
Рис. 1. Прогноз валового сбора на основе линейного тренда
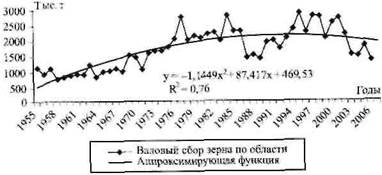
Рис. 2. Прогноз валового сбора на основе полиномиального (2-й степени) тренда
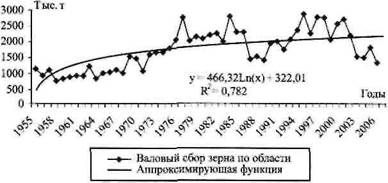
Рис. 3. Прогноз валового сбора на основе логарифмического тренда
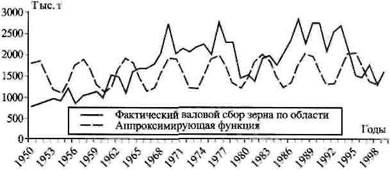
Рис. 4. Прогноз валового сбора на основе комбинированной функции
y = 1444,9+ 4,94t + 405,57sint, R2 = 0,84
y - значение ряда динамики, t - время; r - множественный коэффициент корреляции; R2 - коэффициент детерминации, характеризующий долю дисперсии результативного признака у, объясняемую трендом, в обшей дисперсии результативного признака

Рис. 5. Прогноз валового сбора на основе комбинированной функции
y = 1335,51+ 10,81lnt+ 239.39sint, R2 = 0,92
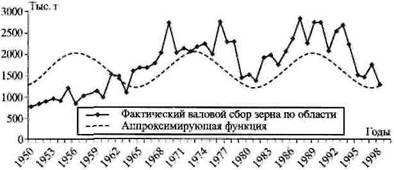
Рис. 6. Прогноз валового сбора на основе комбинированной функции
y = 1626,63 - 440,59 cos 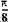 , R2 = 0,87
, R2 = 0,87
Для обоснованности прогноза методом трендовой экстраполяции были рассмотрены характеристики полученных аналитических выравнивающих функций (см. табл. на с. 398).
Характеристики выравнивающих функций для динамического ряда валового сбора зерновых
| Обозначение функции | Вид аппроксимирующей функции | Прогнозируемый на 2007 год валовый сбор (r = 50) | Стандартное отклонение | Коэффициент корреляции | F-критерий Фишера | Коэффициент автокорреляции ряда |
| а | y = 26,35t + 1015,6 | 450,2 | 0,52 | 1,15 | 0,13 | |
| б | y = -1,142t2 + 87,42t+ 469,53 | 369,1 | 0,76 | 4,13 | 2,45 | |
| в | у = 466,32 lnt + 322,0 | 410,9 | 0,78 | 1,92 | 1,18 | |
| г | y = 535,0 t0,31 | 460,1 | 0,64 | 3,13 | 2,17 | |
| д | y = 1335,51+ 10,81 lnt + 239.39sint | 278.2 | 0,92 | 5,56 | 1,97 | |
| е | y = 1626,63- 440,59 cos 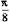
| 212.5 | 0,87 | 3,89 | 1,63 | |
| ж | y = 1444,9 + 4,94t + 405,57sint | 301,2 | 0,84 | 4,12 | 1,91 |
Как показывают данные табл. 2, не все из выравнивающих функций можно использовать для прогнозирования. При оценке надежности уравнения регрессии фактический уровень критерия Фишера (Fфак) для функций а, в, г меньше его теоретического значения (Fтеор). Fтеор= 3,15 - 3,23 при уровне значимости 0,05. Это свидетельствует о том, что построенные уравнения неадекватно отражают сложившуюся в исследуемом ряду динамики тенденцию. В остальных функциях фактическое значение F-критерия больше табличного, т. е. каждая из связей считается значимой. Анализ коэффициента корреляции позволяет утверждать, что связь между аппроксимирующими аналитическими функциями а и г и фактическими данными слабая (коэффициент меньше 0,7). Близость полученных коэффициентов детерминации (квадрата коэффициента корреляции) к единице свидетельствует о наличие тесной связи (уравнения д, е, ж). Проверка на наличие автокорреляции зависимости последующих уровней ряда от предыдущих осуществлялась по критерию Дарбина-Уотсона. Если этот критерий равен 0, имеется полная положительная автокорреляция, 2 - автокорреляция отсутствует, 4 - полная отрицательная автокорреляция. В соответствии с этим критерием незначительная положительная автокорреляция, которую можно не исключать из взаимосвязи, присутствует в функциях б, г, д, ж.
Функции а и в без исключения автокорреляции применять для прогнозирования невозможно.
Таким образом, функции б, д, е, ж хорошо выравнивают исходный динамический ряд и их можно применять для прогнозирования валового сбора зерна в области. Из перечисленных функций минимальное стандартное отклонение S = 212,5 имеет функция н = 1626,63 - 440,59cos  t.
t.
Прогнозное значение валового сбора зерна на 2007 г. составляет 1312 тыс. т. Ошибка прогноза рассчитана по формуле 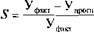 и составляет 4,24%, где
и составляет 4,24%, где
Уфакт - фактическое значение валового сбора, Упрогн - прогнозное значение.
Полученная ошибка прогноза свидетельствует о высокой точности использованного метода прогнозирования.
Глава 3
Решение задачи 3.1.
Показатель расхода инвестиционных средств 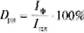 = ((12 + 0,5) / 12) • 100% = 104,16%
= ((12 + 0,5) / 12) • 100% = 104,16%
Показатель производственного ресурсосбережения Dпр = 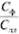 100%, Dпр = ((80 - 80 • 0,1375) / 80) • 100% = 86,25%.
100%, Dпр = ((80 - 80 • 0,1375) / 80) • 100% = 86,25%.
Решение задачи 3.2.
По формуле Dкн = 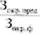 - 100% определяем показатель квалификации научных кадров: Dкн = (16 / 13,6) • 100% = 117,6%.
- 100% определяем показатель квалификации научных кадров: Dкн = (16 / 13,6) • 100% = 117,6%.
Решение задачи 3.3.
Объем продаж (выручку) от реализации инновационной продукции как сумму полной себестоимости и чистой прибыли Vип.ф = 46 + 71,4 = 117,4 тыс. руб.
Показатель исполнения маркетинговых прогнозов Dмп= 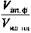 • 100% = (117,4 / 98,3) • 100% = 119,4%.
• 100% = (117,4 / 98,3) • 100% = 119,4%.
Показатель результативности инновационного развития Dир = 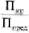 • 100% = (71,4 / 98,3) • 100% = 72,6%.
• 100% = (71,4 / 98,3) • 100% = 72,6%.
Решение задачи 3.4.
Показатель расхода инвестиционных средств
Dри = 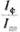 • 100% = (23 800 / 21 000) • 100% =113,3%.
• 100% = (23 800 / 21 000) • 100% =113,3%.
Показатель производственного ресурсосбережения
Dпр = 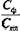 • 100% = (91 000 / 100 000) • 100% = 91%.
• 100% = (91 000 / 100 000) • 100% = 91%.
Глава 4
Решение задачи 4.1.
Цена покупки компанией акций фирмы равна 6 + (6 • 50 / 100) = 9 руб.
Меновое соотношение для акций составляет 9/45 = 0,2.
Количество акций, которые должна дополнительно выпустить компания для обмена их на акции фирмы, равно 0,2 30 = 6 тыс. акций
Решение задачи 4.2.
Цена фирмы определяется по формуле Ц = (ч / n) - K, где ч - годовая сумма чистой прибыли, руб.; n - размер ставки банковского процента за кредит, в долях единицы; K - балансовая стоимость активов фирмы, руб.
Ц = (10,08 / 0,28) - 25 = 11 млн. руб.
Решение задачи 4.3.
Сумма добавочного капитала равна 4,5 - 3 = 1,5 млн. руб.
Стоимость гудвилла составляет 20 - 13,5 - 1,5 = 5 млн. руб.
Решение задачи 4.4.
Цена фирмы Ц = (ч / n) - К = (54,31 / 0,15) - 72 = 290,06 млн. руб.
Глава 5
Решение задачи 5.1.
Затраты С1б = Р1б + (Отр + Несн) + Аоб+ Н1р= 93 + (12 +5,8) + 10 + + 37,2= 158 тыс. руб.
Решение задачи 5.2.
Определим общий размер затрат на реализацию стратегии:
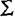 Сy = С1y + С2y + С3y + С4y = 31 + 57 + 95 + 73 = 256 тыс. руб.
Сy = С1y + С2y + С3y + С4y = 31 + 57 + 95 + 73 = 256 тыс. руб.
Решение задачи 5.3.
Затраты С2y = Р2y +(Отр + Несн) + А2об + Н2y =127 + 15 + 7.2 + 12,5 + 46,9 = 208.6 тыс. руб.
Решение задачи 5.4.
Обший размер затрат на реализацию стратегии по формуле: 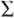 Сб = С1б + С2б + С3б + С4б. Имеем С4б = Р4б + (Отр + Несн) + А4об + Н4р = 233 + 31 + 14,5 + 27 + 96,7 = 402,2 тыс. руб.
Сб = С1б + С2б + С3б + С4б. Имеем С4б = Р4б + (Отр + Несн) + А4об + Н4р = 233 + 31 + 14,5 + 27 + 96,7 = 402,2 тыс. руб.
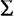 Сб = 81 + 143 + 257 + 402,2 = 883,2 тыс. руб.
Сб = 81 + 143 + 257 + 402,2 = 883,2 тыс. руб.
Глава 6
Решение задачи 6.1.
Средняя численность занятых в сфере НИР и ОКР:
Пн = Чнг + Чп - Чк = 56 - 1 +4=59.
Коэффициент персонала, занятого в НИР и ОКР, составляет:
Kпр = 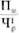 = 59 / 261 = 0,22.
= 59 / 261 = 0,22.
Вывод: для предприятия целесообразна стратегия лидера.
Решение задачи 6.2.
Определим коэффициент освоения новой техники по формуле:
Kот= 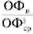 .
.
ОФср = 564,560 + 887,954 + 124,743 = 1577,257 млн. руб.
Kот = 743,241 / 1577,258 = 0,47.
По результатам расчетов можно сделать вывод, что предприятие активно осваивает новую технику, своевременно осуществляет модернизацию и техническое перевооружение производства. Для предприятия целесообразна стратегия лидера.
Решение задачи 6.3.
Коэффициент имущества, предназначенного для НИР и ОКР, определим по формуле:
Ооп = 223 693,16 + 61,48 = 223 754,64 тыс. руб.
Kни = 223 754,64 / 1 324 744,6 = 0,17.
Вывод: предприятию целесообразно выбрать стратегию последователя.
Решение задачи 6.4.
Общая себестоимость новой продукции и продукции, произведенной с использованием новой технологии, составляет сумму постоянных и переменных издержек:
С = 9,907 + 6.605 = 16,512 млн. руб.
Выручка от реализации данной продукции:
В = 16,512 + 16 5120,15 = 18,989 млн. руб.
По формуле Kвп = 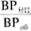 находим коэффициент внедрения новой продукции Kвп = 18,989 / 35,296 = 0,538.
находим коэффициент внедрения новой продукции Kвп = 18,989 / 35,296 = 0,538.
Вывод: предприятие параллельно с освоением новой техники эффективно внедряет усовершенствованные продукты и услуги.
Глава 7
Решение задачи 7.1.
Определим долю затрат каждой команды по формуле: ДЗki = 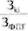
ДЗk1 = 3511 / 10 338 = 0,34.
ДЗk2 = 3920 / 10 338 = 0,38.
ДЗk3 = 2907 / 10 338 = 0,28.
Определим долю каждой команды в совокупной чистой прибыли по формуле: ДПki = 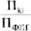
ДПk1 = 510/1522 = 0,33.
ДПk2 = 492/1522 = 0,32.
ДПk3 = 517/1522 = 0,34.
Решение задачи 7.2.
Определим среднюю эффективность по формуле:
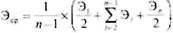
Э1 = 45 / 90 = 0,5.
Э2 = 32 / 60 = 0,53.
Э3= 51 / 80 = 0,64.
Э4 = 29 / 70 = 0,41.
Тогда Эср = (0,5 / 2 + 0,53 + 0,64 + 0,41 / 2) / 3 = 0,54.
Показатель взаимодействия ПВ = 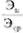 = 0,6 / 0,54 =1,1.
= 0,6 / 0,54 =1,1.
Решение задачи 7.3.
Определим среднюю эффективность по формуле:
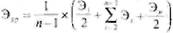
Э1=25 / 80 = 0,31.
Э2 = 30 / 90 = 0,33.
Э3 = 10 / 50 = 0,20.
Э4 = 34 / 70 = 0,49.
Тогда Эср = (0,31 / 2 + 0,33 + 0,20 + 0,49 / 2) / 3 = 0,31.
Интегральная эффективность технологической цепочки:
Эи = 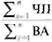 = (25 + 30 + 10 + 34) / (80 + 90 + 50 + 70) = 0,34.
= (25 + 30 + 10 + 34) / (80 + 90 + 50 + 70) = 0,34.
Показатель взаимодействия (ПВ) рассчитывается по формуле:
ПВ = 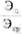 = 0,34 / 0,31 = 1,1.
= 0,34 / 0,31 = 1,1.
Решение задачи 7.4.
Чистая прибыль ФПГ ПФПГ = ( 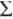 ЧПi) + ЧПупр =(211+305 + 190 + 178) + 310= 1194 млн. руб.
ЧПi) + ЧПупр =(211+305 + 190 + 178) + 310= 1194 млн. руб.
Эффективность ФПГ ЭФПГ = 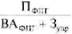 = 1194 / (1380 + 530) = 0,625 млн. руб.
= 1194 / (1380 + 530) = 0,625 млн. руб.
Глава 8
Решение задачи 8.1.
Пусть статистические характеристики каждого из туров экспертной оценки выглядят так, как приведено в таблицах 1-3 соответственно по турам.
В результате первого тура были определены следующие данные (табл. 1).
Таблица 1
Первый тур опроса
| Экспертные данные, тыс. т | |||||||
| Ранжированный ряд | |||||||
| Экспертные данные, тыс. т | |||||||
| Ранжированный ряд |
Тогда среднее значение оценки:
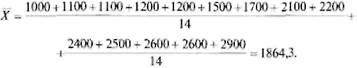
Среднее квадратичное отклонение оценок:
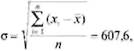
где n - число экспертов, участвующих в экспертизе: xi - оценка эксперта. Коэффициент вариации v = 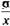 100 =
100 = 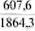 100 = 35,0%.
100 = 35,0%.
Нижний квартиль Q0,25= 1200. Верхний квартиль Q0,75 = 2500.
Медиана Me = 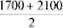 = 1900,0.
= 1900,0.
Результаты второго тура опроса представлены в табл. 2.
Таблица 2
Второй тур опроса
| Экспертные данные, тыс. т | |||||||
| Ранжированный ряд | |||||||
| Экспертные данные, тыс. т | |||||||
| Ранжированный ряд |
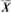 = 1517,8; Q0,25 = 1100;
= 1517,8; Q0,25 = 1100; 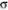 = 511,16;
= 511,16;
Me = 1350; Q0,75 = 2000; v = 33,6%.
Результаты по третьему туру опроса представлены в табл. 3.
Таблица 3
Третий тур опроса
| Экспертные данные, тыс. т | |||||||
| Ранжированный ряд | |||||||
| Экспертные данные. тыс. т | юно | ||||||
| Ранжированный ряд |
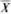 = 1221.4; Q0,25 = 1100;
= 1221.4; Q0,25 = 1100;  = 160,9;
= 160,9;
Me =1200; Q0,75 = 1350; v = 13,1%.
Общие результаты экспертизы по турам представлены в табл. 4.
Таблица 4
Общие результаты экспертизы по турам
| Тур | Интервал | Средняя оценка в туре | Дисперсия | Вариация, % |
| 1200 ... 2500 | 1828,5 | 426 581,52 | ||
| 1100... 2000 | 1517,8 | 261 284,54 | 33,6 | |
| 1100 ... 1350 | 1221,4 | 25 888,81 | 13,1 |
Поскольку после третьего тура достигнута высокая степень согласованности мнений экспертов (v = 13,1 %), можно считать экспертизу завершенной и сделать вывод, что валовой сбор зерна в Курской области в 2007 г. составит 1200 тыс. т. что на 90 тыс. т меньше, чем в 2006 г.
Решение задачи 8.2.
Упорядочим результаты по степени их важности и присвоим им значения от 7 до 1:
v1 = 7, v2 = 6, v3 = 5, v4 = 4, v5 = 3, v6= 2, v7 = 1.
Сравниваем v1с суммой v2 + v3 + ... + v7; v1 = 7; v2 + v3+ ... + v7 = 21. Оставляем v1= 7.
Сравниваем v2 с суммой v3 + v4 + ... + v7; v2 = 6; v3 + v4 + ... + v7 = 15. Оставляем v2 - 6.
Сравниваем v3 с суммой v4 + v5 + ... + v7; v3 = 5; v4 + v5 + ... + v7 = 10. Оставляем v3 = 5.
Сравниваем v4 с суммой v5 + v6 + v7; v4 = 4; v5 + v6 + v7 = 6. Полагая, что v4 и v5 + v6 + v7 равнозначны, примем v4 = 6, соответственно v1 = 9, v2 = 8, v3 = 7. Начинаем сравнения с начала.
Сравниваем v5 с суммой v6 + v7; v5 = 3; v6 + v7 = 3. Оставляем v5 = 3.
Сравниваем v6 с v7: v6 = 2; v7 = 1. Оставляем v6 = 2.
Рассчитаем нормированные коэффициенты:
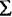 vi = 36; v'1 = 7 / 36; v'2 = 6 / 36; v3' = 5 / 36; v4' = 4 / 36; v5' = 3 / 36; v6' = 2 / 36; v7' = 1 / 36.
vi = 36; v'1 = 7 / 36; v'2 = 6 / 36; v3' = 5 / 36; v4' = 4 / 36; v5' = 3 / 36; v6' = 2 / 36; v7' = 1 / 36.
Проведем оценку стратегий по отношению к достижению каждой из семи целей:
| Цель | Стратегия | ||
| A | B | C | |
| 0,8 | 0,8 | 0,8 | |
| 0,7 | 0,7 | 0,8 | |
| 0,6 | 0,7 | 0,8 | |
| 0,4 | 0,5 | 0,6 | |
| 1,0 | 0,4 | 0,3 | |
| 0,8 | 0,9 | 0,7 | |
| 0,7 | 0,8 | 0,6 |
Рассчитаем полезности стратегий:
ПА= (0,8 х 9 + 0,7 х 8 + 0,7 х 7 + 0,4 х 6 + 0,1 х 3 + 0,8 х 2 + 0,7 х 1) / 36 = 0,63;
ПB =(0,8 х 9 + 0,7 х 8 + 0,7 х 7 + 0,5 х 6 + 0,4 х 3 + 0,9 х 2 + 0,8 х 1) / 36 = 0,68;
ПC = (0,8 х 9 +0,8 х 8 + 0,8 х 7 + 0,6 х 6 + 0,3 х 3 + 0,7 х 2 + 0,6 х 1) / 36 = 0,71.
Вывод: все три стратегии достаточно близки по полезности, однако для достижения указанных инновационных целей организации целесообразно выбрать стратегию C или стратегию B.
Решение задачи 8.3.
Таблицы, приведенные в условии, трансформируем в виде платежных матриц:
Стратегии фирмы и поставщика № 1
| Стратегия фирмы | Стратегия поставщика № 1 | |
| П1 | П2 | |
| С1 | -500 | -700 |
| С2 | -600 | -650 |
| С3 | -650 | -950 |
| С4 | -1100 | -600 |
Стратегии фирмы и поставщика № 2
| Стратегия фирмы | Стратегия поставщика № 2 | |
| П1 | П2 | |
| С1 | -650 | -850 |
| С2 | -730 | -930 |
| СЗ | -780 | -1230 |
| С4 | -1380 | -730 |
Стратегии фирмы и поставщика № 3
| Стратегия фирмы | Стратегия поставщика № 3 | |
| П1 | П2 | |
| C1 | -800 | -1000 |
| C2 | -950 | -1300 |
| C3 | -1000 | -1600 |
| C4 | -1500 | -950 |
Стратегии фирмы и поставщика № 4
Дата добавления: 2019-02-07; просмотров: 873;
