Финансовые модели оценки и управления капиталом

Модель Гордона

Дивиденды, выплачиваемые по обыкновенным и привилегированным акциям, зависят от размера полученной чистой прибыли, и в любом случае для их выплаты требуется решение совета директоров и общего собрания. Поэтому можно предположить, что акционерный капитал не имеет стоимости. Действительно, в отличие от владельцев облигаций акционеры могут не получать ежегодный текущий доход вообще, т.е. корпорация может ничего не выплачивать владельцам собственного капитала. Однако такая форма функционирования долго существовать не может, невозможно будет привлечь дополнительный новый капитал. Владельцы собственного капитала соглашаются на отсутствие или снижение дивидендной доходности только при условии возможного роста отдачи в будущем (в виде дивидендов или прироста капитала).

Стоимость акционерного капитала, таким образом, есть годовая процентная ставка, которая платится для поддержания текущей рыночной оценки акционерного капитала. Если корпорация обеспечивает меньшую доходность, чем требуемая, акционеры избавляются от акций и превышение предложения акций над спросом приводит к падению цены. Текущая рыночная оценка акционерного капитала падает. Особенность акционерного капитала заключается в том, что часть платы за него может быть представлена в денежной форме (дивиденды, выплачиваемые деньгами), а часть в виде накопленного увеличения капитала.

Акционеры корпорации, не использующей финансовый рычаг (с нулевым финансовым рычагом), требуют на вложенные средства (т.е. на весь капитал корпорации) доходность, которая покрывала бы два элемента:

1) временную стоимость денег, т.е. компенсировался бы отказ от текущего получения денежных средств в пользу ожидания получения их в будущем учетом инфляции;

2) риск, связанный с получением денежных средств.

Таким образом, ставка дисконтирования должна отражать обе состав-ляющие требуемой доходности: доходность по безрисковым инвестиционным решениям аналогичного срока и премию (надбавку) за риск.

Для обоснования требуемой доходности широко применяются две равновесные модели: модель Гордона — модель оценки акции при предположении постоянного роста дивидендов.

Модель Гордона для оценки акции по текущему дивиденду:

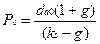
Предполагается, что инвестируется ежегодно фиксированная величина чистой прибыли (дивидендный выход неизменен по годам). Инвестиции обеспечивают доходность, что позволяет корпорации ежегодно увеличивать чистую прибыль с темпом роста g. Предполагается, что требуемая доходность владельцев капитала превышает темп роста g (это естественное предположение, так как компании не могут на бесконечном временном промежутке наращивать прибыль и дивиденды высоким темпом).

Переписав выражение цены акции в модели Гордона, получаем выражение для требуемой доходности:

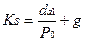
Требуемая доходность по акционерному капиталу состоит из двух элементов: прогнозируемой дивидендной доходности и ожидаемого темпа роста прибыли и дивидендов в результате реализации инвестиционного решения.

Важно отметить, что это выражение для K_S основывается на текущей рыночной оценке акции и не включает специфические ожидания относительно роста. Рост определяется дивидендным выходом и ожидаемой доходностью. Очевидно, что это очень сильное ограничение модели. В зависимости от того, насколько темп роста, обеспечиваемый инвестиционным решением, будет близок к ныне наблюдаемому темпу роста, можно говорить о корректной оценке требуемой доходности.

Например, если предположить, что акция корпорации верно оценена рынком в 3 долл. и дивиденд на акцию составил в текущем году 0,2 долл. на акцию, то при темпе роста g = 12%, проецируя прошлый рост на будущее, можно рассчитать требуемую доходность по акционерному капиталу: ks - 0,2 х 1,12 /3 + 0,12 = 0,195 (19,5%).

Существенные ограничения модели Гордона являются не единственными недостатками рассмотренного подхода к оценке стоимости акционерного (собственного) капитала. При его использовании необходимо учитывать следующее.

1. Рассчитанное значение ks зависит от выбранного временного промежутка. Темп роста g рассчитывается по прошлым годам и поэтому в значительной степени зависит от временного отрезка расчета.

Более правильно использовать данные на большом временном промежутке, хотя общий недостаток модели сохраняется прошлый рост не является абсолютно верным индикатором будущего роста. Как вариант преодоления этого недостатка в ряде случаев используются прогнозируемые оценки g, однако общерыночные изменения могут исказить полученный результат.

2. Рассчитанное значение зависит от выбора даты оценки текущей цены P₀. Обычно в расчетах используется значение P₀ на конец финансового года. Публикуемые данные по курсам акций часто не фиксируют дату выплаты дивиденда, и ошибкой будет использовать данные по цене после эксдивидендной даты. Сложность заключается в том, что ряд компаний выплачивают дивиденды несколько раз в году. В этом случае расчет требует корректировки имеющихся данных. Например, если в ближайшие два месяца ожидаются дивиденды в размере 0,05 долл. на акцию, то можно предположить падение цены после экс-дивидендной даты на 0,05 долл.

3. Результаты расчетов зависят от краткосрочных изменений цены.

4. Налоговые выплаты обязательно должны учитываться при принятии инвестиционных решений. Налоговые платежи учитываются при оценке денежных потоков, генерируемых долгосрочными активами, в которые инвестируются денежные средства. Очевидна необходимость дисконтирования посленалоговых денежных потоков на скорректированную на налоговые платежи стоимость капитала.

Модель У.Шарпа

Ожидаемую доходность актива можно определить на основе индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависят от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель была предложена У.Шарпом в середине 60-х годов. Цель ее разработки состояла в том, чтобы упростить процесс определения эффективной границы Марковца, сократив количество необходимых вычислений. У.Шарп назвал модель диагональной. В модели представлена зависимость между доходностью актива и значением рыночного индекса. Она предполагается линейной. Уравнение модели можно записать как:

Случайную компоненту доходности at можно разделить на две части:

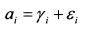
y_i является константой и представляет собой ожидаемую доходность актива при отсутствии воздействия на него рыночных факторов. ६_i - это случайная величина со средним значением равным нулю. С учетом сказанного модель принимает вид:

В формулу вводится независимая случайная переменная (ошибка): она показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней равно нулю, дисперсия постоянна, ковариация со значением рыночного индекса равна нулю; ковариация с нерыночным компонентом доходности других активов равна нулю, т.е. 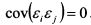. В силу центральной предельной теоремы ६ распределена нормально, поскольку на нее оказывает влияние большое количество разных факторов.

По условиям модели ожидаемое значение величины ६ равно нулю. Поэтому ожидаемое значение доходности актива E(r_i) определяется как:

Модель получила название диагональной, поскольку риск портфеля можно представить с помощью ковариационной матрицы, в которой все значения равны нулю, кроме значений, расположенных на главной диагонали. Поясним сказанное.

Доходность портфеля равна:

Подставим в формулу (3.17) формулу (3.16):

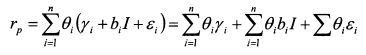
ИЛИ

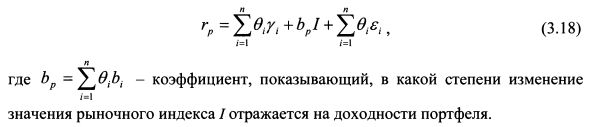
На основе формулы (3.18) дисперсия доходности портфеля равна:

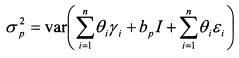
или

Формулу (3.19) можно записать в матричной форме как:

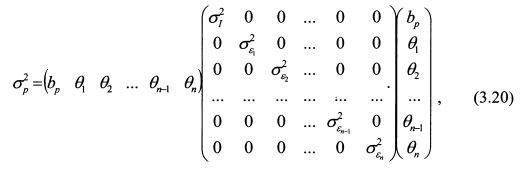
Из выражения (3.20) видно, что в ковариационной матрице по главной диагонали стоят дисперсия рыночного индекса и дисперсии специфических рисков активов портфеля. Остальные значения матрицы равны нулю.

В формуле (3.16) Дж. Трейнор заменил значение индекса показателем его доходности, чтобы оперировать однопорядковыми величинами зависимой и независимой переменных. Данную модель называют рыночной моделью. Ее уравнение имеет вид:

Если уравнение (3.21) применить для определения ожидаемой доходности портфеля, оно примет вид:

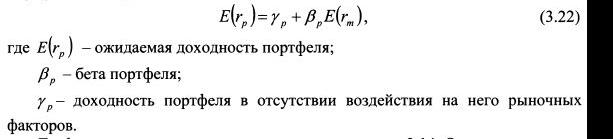
Графически рыночная модель представлена на рисунке 4.1. Она показывает зависимость между доходностью рыночного индекса (r_m) и доходностью актива (r_i и представляет собой прямую линию). Дж. Трейнор назвал ее линией характеристики. Независимой переменной выступает доходность рыночного индекса. Линия характеристики есть не что иное, как линия регрессии доходности актива на доходность рыночного индекса. Поэтому на основе метода наименьших квадратов параметры рассчитываются как:

Пример.

Средняя доходность актива А равна 20%, средняя доходность рыночного индекса - 17%, ковариация доходности актива и индекса составляет 0,04, дисперсия индекса 0,09. Определить уравнение рыночной модели.

Решение.

Бета актива А равна:

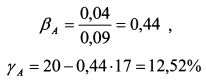
Уравнение рыночной модели имеет вид:

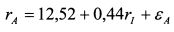
На рисунке 4.1 точками показаны конкретные значения доходности актива А и рынка для различных моментов времени в прошлом.

На рисунке 4.1 представлен случай, когда бета положительна, и поэтому график рыночной модели направлен вправо вверх, т. е. при увеличении доходности рыночного индекса доходность актива будет повышаться, при понижении - падать. При отрицательном значении беты график направлен вправо вниз, что говорит о противоположном движении доходности индекса и актива. Более крутой наклон графика говорит о высоком значении беты и большем риске актива, менее крутой наклон - о меньшем значении беты и меньшем риске.

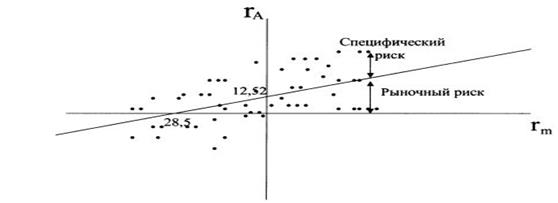
Рисунок 4.1 – Линия характеристики

Модель Арбитража

В 1976 г. С.Росс предложил модель оценки доходности активов, которая получила название "Арбитражная теория оценки стоимости" (Arbitrage pricing theory - APT). В рамках модели все инвесторы имеют одинаковые ожидания относительно ожидаемой доходности активов и вероятностных распределений значений факторов риска, отсутствуют ограничения на короткие продажи. Как отмечают Р.Ролл и С.Росс, в качестве первого принципа модели выступает линейный процесс формирования доходности активов. В отличие от САРМ, в APT не делается акцент на какой-либо особый портфель, не учитывается положение об эффективности рыночного портфеля, не делаются особые предположения о функции полезности инвестора, а лишь предполагается ее монотонность и выпуклость. Модель не ограничивается одним временным периодом.

Свои рассуждения С.Росс начинает с предположения о том, что инвесторы считают: доходности активов определяются линейной моделью с факторами риска:

Коэффициент чувствительности определяется как и в модели САРМ по формуле:

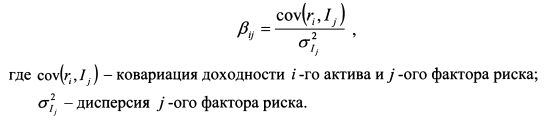
В модели предполагается, что количество активов на рынке намного больше количества факторов, влияющих на доходность активов.

Модель получила название арбитражной, так как она накладывает арбитражные ограничения на доходности активов. Это означает, что в случае нарушения равновесия на рынке, т.е. возникновения нелинейных соотношений между риском и доходностью активов, можно заработать арбитражную прибыль. В свою очередь действия арбитражеров восстановят равновесие. Арбитражная прибыль получается в результате формирования арбитражного портфеля.

С.Росс рассматривает инвестора, который владеет некоторым портфелем и анализирует варианты создания различных арбитражных портфелей на его основе. Арбитражный портфель характеризуется тем, что его формирование не связано с дополнительными издержками, так как покупка одних активов финансируется за счет средств от продажи других активов в портфеле. Таким образом, в арбитражном портфеле сумма всех удельных весов активов равна нулю:

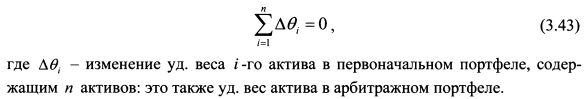
На основе уравнения (3.42) дополнительный доход, который инвестор получит от арбитражного портфеля, равен:

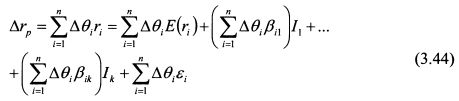
В уравнении (3.44) последнее слагаемое представляет собой специфический риск. Для широко диверсифицированного портфеля его значение практически равно нулю, поэтому им можно пренебречь.

По определению арбитражный портфель не должен быть восприимчив ни к одному фактору риска. Следовательно, удельные веса активов в портфеле можно подобрать для каждого фактора таким образом, чтобы исключить и рыночный риск. Поэтому портфель характеризуется условием:

В результате, доходность, которую получит инвестор от формирования арбитражного портфеля при нарушении равновесия на рынке, определяется только первым слагаемым в уравнении (3.44) и составляет:

В условиях равновесия доходность арбитражного портфеля должна быть равна нулю, т.е.:

Условия (3.47), (3.45) и (3.43) определяют следующий вид зависимости ожидаемой доходности актива от факторов риска:

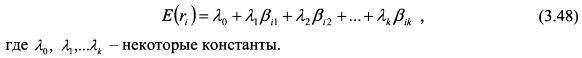
Чтобы увидеть данную зависимость, умножим уравнение (3.48) для каждого актива на значение его удельного веса в арбитражном портфеле и просуммируем полученные значения для всех активов. Для наглядности проделаем это для портфеля из трех активов при существовании двух факторов риска и, соответственно, двух коэффициентов чувствительности к факторам риска. Для каждого актива получаем результат:

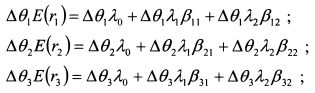
Суммируем:

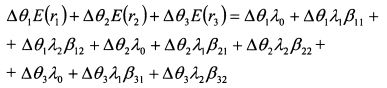
или

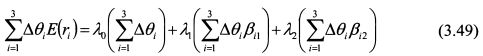
Если выполнены условия (3.43) и (3.45), то слагаемые в правой части (3.49) равны нулю, и, следовательно, выполняются зависимости (3.47) и (3.48). Зависимость (3.48) является центральным выводом модели APT.

Зависимость (3.48) можно получить и на основе стандартных рассуждений, не допускающих арбитражных ситуаций на рынке. Между риском и доходностью активов должна выдерживаться определенная закономерность. Поскольку нерыночный риск устраняется за счет диверсификации, то зависимость будет отражать только рыночный риск. Если зависимость между риском и доходностью активов не линейна, открывается возможность получить арбитражную прибыль. Проведем рассуждения для случая, когда доходности активов зависят только от одного фактора риска. Допустим, между доходностями активов и их рыночным риском, представленным коэффициентом бета, не выдерживается линейная зависимость. Пусть фактическая ситуация представлена на рисунке 4.2, т.е. бумаги располагаются на некоторой кривой. Ожидаемые доходности портфелей и их риски, измеренные коэффициентом бета, являются средневзвешенными величинами. Поэтому инвестор может образовать два портфеля. Он осуществит короткую продажу бумаги С и купит бумагу В таким образом, чтобы доходность первого портфеля составила величину E(r1). Он также осуществит короткую продажу бумаги D и купит бумагу А таким образом, чтобы доходность второго портфеля составила величину E(r2). После этого инвестор продаст менее доходный второй портфель и купит более доходный первый портфель. Арбитражная прибыль составит разницу между E(r1) и E(r2). Для корректности рассуждений необходимо учесть еще один момент. Если каждый портфель построен только из двух бумаг, то он характеризуется высоким нерыночным риском. Поэтому в рассмотренной ситуации следует формировать широко диверсифицированные портфели. Это можно сделать следующим образом.

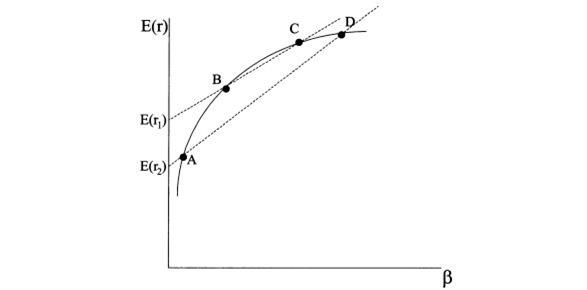
Рисунок 4.2 – Формирование арбитражного портфеля