Предел числовой последовательности
Числовой последовательностью называют правило, по которому каждому натуральному числу 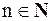 ставится в соответствие действительное (комплексное) число
ставится в соответствие действительное (комплексное) число 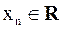
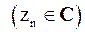 . Последовательность обозначают символом
. Последовательность обозначают символом 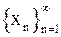 (
( 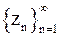 ). Можно сказать, что последовательность является функцией
). Можно сказать, что последовательность является функцией  (
( 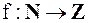 ). Очевидным образом определяются сумма, произведение, частное двух последовательностей. В этом разделе мы будем иметь дело лишь с последовательностями действительных чисел.
). Очевидным образом определяются сумма, произведение, частное двух последовательностей. В этом разделе мы будем иметь дело лишь с последовательностями действительных чисел.
Число  называется пределом последовательности
называется пределом последовательности 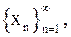 если для любого
если для любого 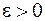 найдётся номер
найдётся номер 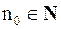 такой, что для любого
такой, что для любого 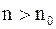 выполняется неравенство
выполняется неравенство 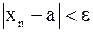 . При этом пишут
. При этом пишут 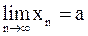 или
или 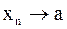 и говорят, что последовательность
и говорят, что последовательность 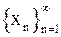 сходится к числу
сходится к числу 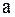 .
.
Если 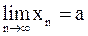 ,
, 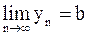 , то: 1)
, то: 1) 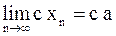 ;
;
2) 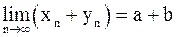 ; 3)
; 3)  ;
;
4) 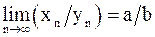 при (
при (  ).
).
Пример 1. Дана последовательность 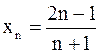 . Найдите: а)
. Найдите: а) 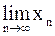 ; б)
; б)  такое, что для всех
такое, что для всех 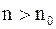 выполняется неравенство
выполняется неравенство 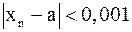 .
.
Решение. а) Имеем 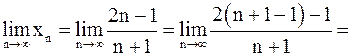
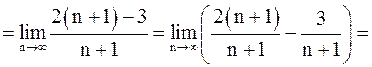
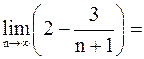
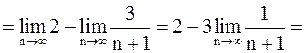
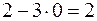 .
.
б) Найдём требуемое  . Из проделанных выше выкладок следует, что
. Из проделанных выше выкладок следует, что  должно быть подобрано так, чтобы для всех
должно быть подобрано так, чтобы для всех 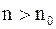
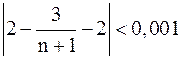 или
или 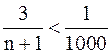 ;
;
отсюда следует 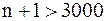 ,
, 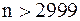 . Следовательно, можно взять
. Следовательно, можно взять 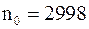 .
.
Последовательность 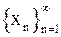 называется бесконечно малой, если
называется бесконечно малой, если 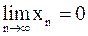 .
.
Последовательность 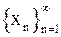 называется бесконечно большой, если для любого
называется бесконечно большой, если для любого 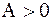 найдётся номер n0 такой, что для любого
найдётся номер n0 такой, что для любого 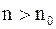 справедливо неравенство
справедливо неравенство 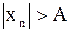 ; записывается это так:
; записывается это так: 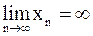 . Если при этом
. Если при этом 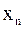 , начиная с некоторого номера, сохраняет положительный (отрицательный) знак, то пишут
, начиная с некоторого номера, сохраняет положительный (отрицательный) знак, то пишут 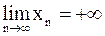 (
( 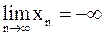 ) .
) .
Важную роль играет последовательность  Доказывается, что эта последовательность сходится, и ее предел обозначается буквой е; е
Доказывается, что эта последовательность сходится, и ее предел обозначается буквой е; е 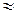 2,718.
2,718.
2. Элементарные функции
К элементарным функциям относятся:
1) простейшие элементарные функции: постоянная с, степенная 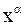 , показательная
, показательная 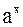 , логарифмическая
, логарифмическая 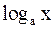 , тригонометрическая
, тригонометрическая  , обратные тригонометрические
, обратные тригонометрические 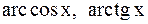 ;
;
2) все функции, получающиеся из простейших элементарных функций путем применения конечного числа следующих четырех операций: сложение, умножение, деление, суперпозиция функций (сложная функция).
Пример 2. В класс элементарных функций попадают:
а) многочлен; б) рациональная дробь (отношение двух многочленов); в) 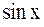 , так как
, так как 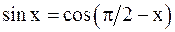 ; г)
; г) 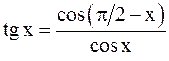 ; д)
; д) 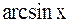 , так как
, так как 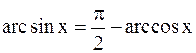 и множество других.
и множество других.
3. Предел функции
Пусть функция  определена во всех точках интервала
определена во всех точках интервала 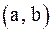 , за исключением, быть может, точки
, за исключением, быть может, точки 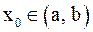 . Число А называется пределом функции
. Число А называется пределом функции  в точке
в точке 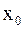 , если для любого
, если для любого 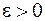 существует число
существует число  такое, что для любого x, удовлетворяющего неравенству
такое, что для любого x, удовлетворяющего неравенству 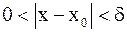 , выполняется неравенство
, выполняется неравенство 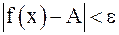 , при этом пишут
, при этом пишут 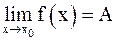 . Можно дать другое, равносильное приведенному, определение: число A называется пределом функции
. Можно дать другое, равносильное приведенному, определение: число A называется пределом функции  в точке x0, если для любой последовательности чисел
в точке x0, если для любой последовательности чисел 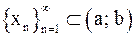 , сходящейся к
, сходящейся к 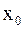 ,
, 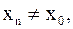
 .
.
Если  определена в интервале
определена в интервале 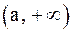 , то число A называется пределом
, то число A называется пределом  при
при 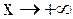 , если для любого
, если для любого 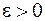 существует число
существует число  , такое, что неравенство
, такое, что неравенство 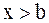 влечет за собой неравенство
влечет за собой неравенство 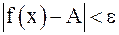 . При этом пишут
. При этом пишут 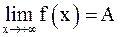 или
или 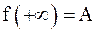 . Аналогично определяется
. Аналогично определяется 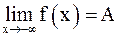 .
.
Число A называют пределом функции  в точке
в точке 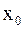 слева (справа) и пишут
слева (справа) и пишут 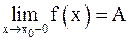 или
или 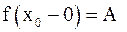
 , или
, или 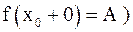 , если для любого
, если для любого 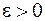 найдется
найдется  такое, что для всех
такое, что для всех 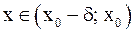 (для всех
(для всех 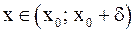 ) справедливо неравенство
) справедливо неравенство 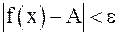 . Число A является пределом
. Число A является пределом  в точке
в точке 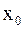 , если совпадают пределы
, если совпадают пределы  в этой точке слева и справа:
в этой точке слева и справа: 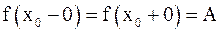 .
.
Если функция  определена в интервале
определена в интервале 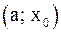 (в интервале
(в интервале 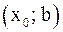 ) и для любого M существует
) и для любого M существует  такое, что для любого
такое, что для любого 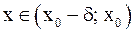 (для любого
(для любого 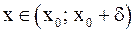 справедливо неравенство
справедливо неравенство 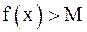 , то говорят, что левый (правый) предел функции
, то говорят, что левый (правый) предел функции  в точке
в точке 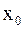 равен
равен 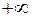 , и при этом пишут
, и при этом пишут 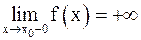 или
или 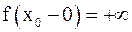
 или
или 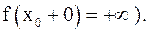 Аналогично определяются
Аналогично определяются 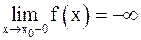 и
и  .
.
Предел функции обладает теми же свойствами, что и предел последовательности: если 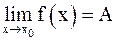 ,
, 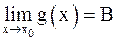 , то
, то
1) 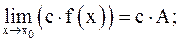
2) 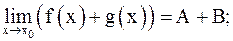
3) 
4) 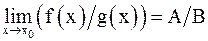
(последнее при 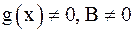 ). То же верно для односторонних пределов.
). То же верно для односторонних пределов.
Пример 3. Доказать, что 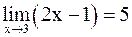 . По данному
. По данному 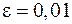 найти
найти  такое, что из неравенства
такое, что из неравенства 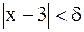 следует
следует  .
.
Решение. Пусть 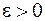 произвольно. Неравенство
произвольно. Неравенство 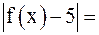
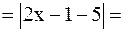
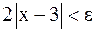 равносильно неравенству
равносильно неравенству  . Поэтому, если по данному
. Поэтому, если по данному 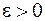 взять
взять  , то из неравенства
, то из неравенства 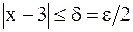 будет следовать неравенство
будет следовать неравенство 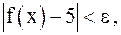 а это и означает, что
а это и означает, что 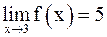 . В частности, для
. В частности, для 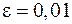 достаточно взять
достаточно взять  .
.
Пример 4.Найти пределы:
а) 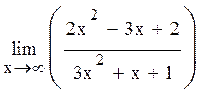 , б)
, б) 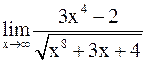 , в)
, в) 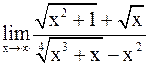 .
.
Решение. а) 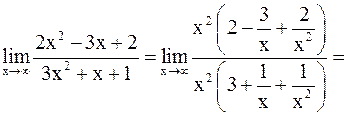
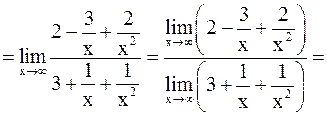
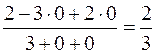 ;
;
б) 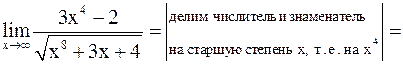

в) 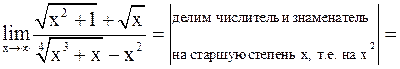
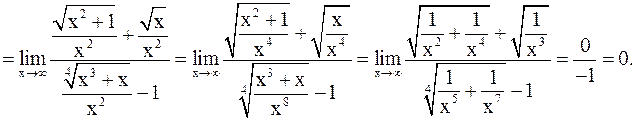
Пример 5. Вычислить:
а) 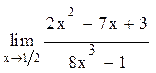 б)
б) 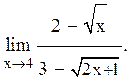
Решение.а)При подстановке 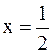 в числитель и знаменатель они обращаются в нуль.
в числитель и знаменатель они обращаются в нуль.
Следовательно, мы имеем неопределенность вида 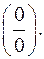
Разложим числитель и знаменатель на множители и перейдем к пределу

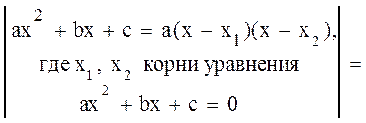
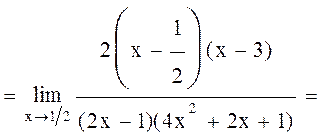

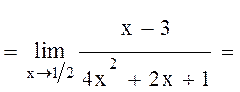

б)В этом примере имеем неопределенность вида 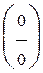 . Умножим числитель и знаменатель на произведение
. Умножим числитель и знаменатель на произведение 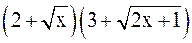 , получим
, получим
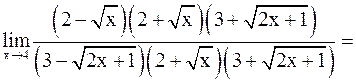
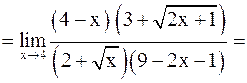
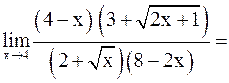
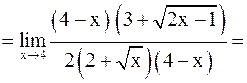
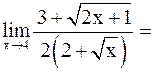

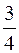 .
.
Пример 6. .
Решение.Имеем неопределенность вида  .
.
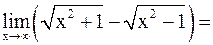
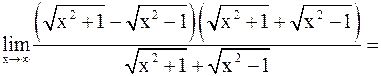
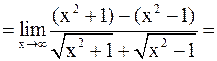
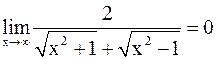 .
.
Имеют место равенства
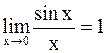 ,
, 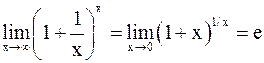 ,
,
называемые первым и вторым замечательными пределами.
Пример 7.Найти:
а) 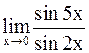 ; б)
; б) 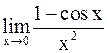 ; в)
; в) 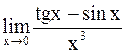 .
.
Решение.а) Применяем первый замечательный предел:
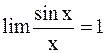 .
.
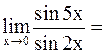
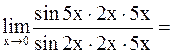
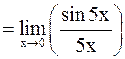
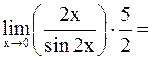
 .
.
б) 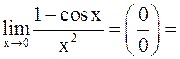
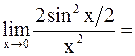
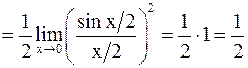 .
. 
в) 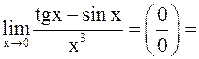
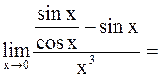
= 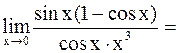
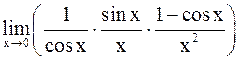
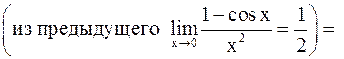
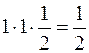 .
.
Пример 8.Найти:
а) 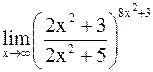 ; б)
; б) 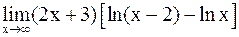 .
.
Решение.
а) 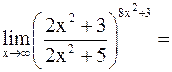
 .
.
В основании прибавим и вычтем единицу
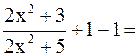
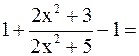
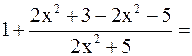
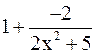 .
.
Тогда 
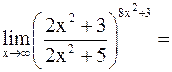
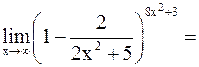

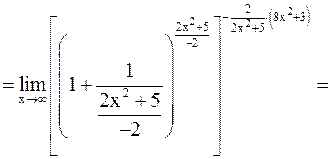
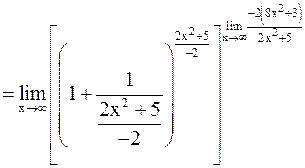 .
.
Вычисляем 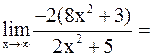
 =
=
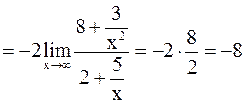 .
.
Тогда 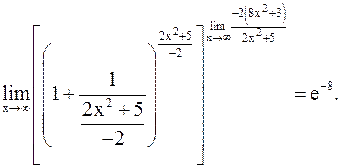
б) 
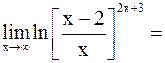
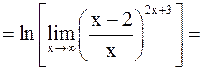

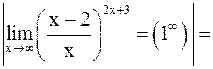
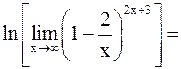
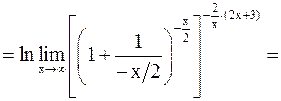

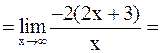
 .
.
Тогда
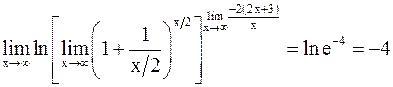 .
.
в) 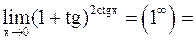
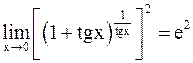 .
.
4. Непрерывность функции
Функция  , определённая в некоторой окрестности
, определённая в некоторой окрестности 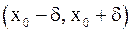 точки
точки 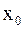 , называется непрерывной в точке
, называется непрерывной в точке 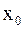 , если
, если 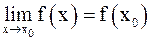 .
.
Другими словами,  непрерывна в точке x0, если выполнены два условия:
непрерывна в точке x0, если выполнены два условия:
1)  определена в некотором интервале, содержащем точку
определена в некотором интервале, содержащем точку 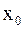 ,
,
2) бесконечно малому приращению аргумента 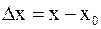 отвечает бесконечно малое приращение функции
отвечает бесконечно малое приращение функции 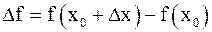 .
.
Функция  непрерывна в точке
непрерывна в точке 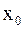 в том и только том случае, если
в том и только том случае, если  .
.
Если функция  непрерывна в каждой точке числового множества X, то говорят, что
непрерывна в каждой точке числового множества X, то говорят, что  непрерывна на множестве X .
непрерывна на множестве X .
Сумма, произведение, частное (при неравенстве нулю знаменателя), суперпозиция непрерывных функций также являются непрерывными функциями.
Функция  терпит разрыв в точке
терпит разрыв в точке 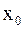 в одном из следующих случаев:
в одном из следующих случаев:
1)  , но
, но 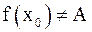 либо
либо 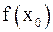 не определено (рис.1); в этом случае говорят, что
не определено (рис.1); в этом случае говорят, что 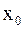 – точка устранимого разрыва;
– точка устранимого разрыва;
2) 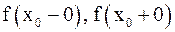 – конечные, но не равные между собой пределы; такая точка называется точкой разрыва первого рода (говорят, что
– конечные, но не равные между собой пределы; такая точка называется точкой разрыва первого рода (говорят, что  терпит в точке
терпит в точке 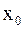 скачок) (рис.2);
скачок) (рис.2);
3) по крайней мере одного из односторонних пределов  в точке
в точке 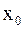 не существует (т.е. не существует конечного предела); в таком случае говорят, что x0 – точка разрыва второго рода (рис.3).
не существует (т.е. не существует конечного предела); в таком случае говорят, что x0 – точка разрыва второго рода (рис.3).
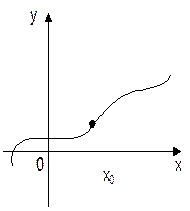 Рис. 1
Рис. 1
| 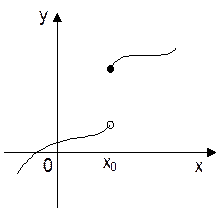 Рис. 2
Рис. 2
|
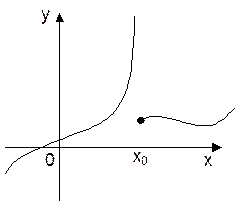 Рис. 3
Рис. 3
|
Все элементарные функции непрерывны в области их определения.
Пример 9.Исследовать на непрерывность функцию
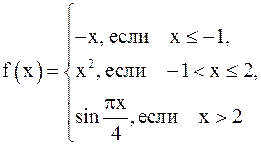
и построить её график.
Решение. Аналитические выражения 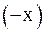 ,
, 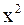 ,
, 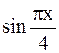 , входящие в определение
, входящие в определение  , задают непрерывные элементарные функции.
, задают непрерывные элементарные функции.
Поэтому  непрерывна всюду, кроме, может быть, точек «склейки»
непрерывна всюду, кроме, может быть, точек «склейки» 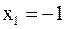 и
и  . Исследуем поведение функции в окрестности этих точек.
. Исследуем поведение функции в окрестности этих точек.
а) 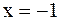 .
.
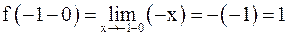 ;
;
 ;
;
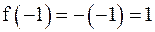 .
.
Так как  , то функция непрерывна в точке x = –1.
, то функция непрерывна в точке x = –1.
б) 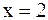 .
.
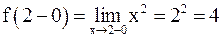 ;
;
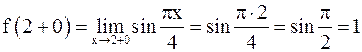 ;
;
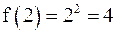 .
.
Так как 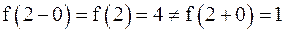 , то
, то  в точке
в точке  терпит разрыв первого рода.
терпит разрыв первого рода.
Сделаем чертёж (рис.4).
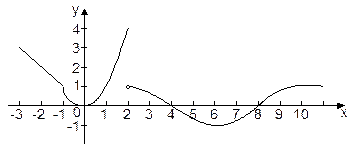
Рис. 4
Пример 10.Исследовать на непрерывность функцию  . Сделать эскиз графика.
. Сделать эскиз графика.
Решение. Функция является элементарной, поэтому непрерывна во всех точках, кроме точек 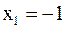 ,
, 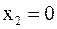 ,
,  , в которых она не определена. Найдём характер разрыва в этих точках.
, в которых она не определена. Найдём характер разрыва в этих точках.
а) 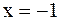 .
.
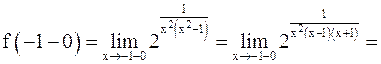
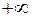 ;
;
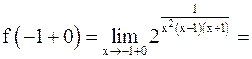
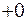
(+0 означает, что  стремится к 0, оставаясь больше 0).
стремится к 0, оставаясь больше 0).
Так как 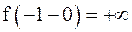 ,
, 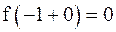 , то
, то  в точке
в точке 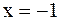 терпит разрыв второго рода.
терпит разрыв второго рода.
б) 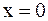 .
.
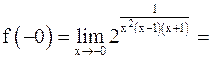
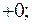
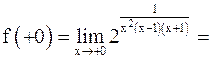
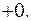
Видим, что 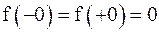 , но
, но 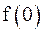 не определена, следовательно,
не определена, следовательно, 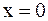 является точкой устранимого разрыва.
является точкой устранимого разрыва.
в) 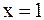 .
.
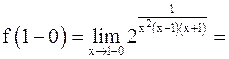
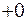 ;
;
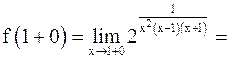

Так как 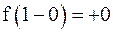 ,
, 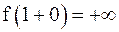 , то
, то 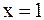 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Для построения эскиза графика исследуем поведение функции при
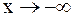 и
и 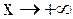 :
:
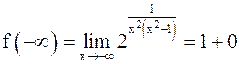 ,
,
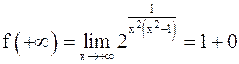
(выражение (1+0) означает, что  стремится к 1, оставаясь
стремится к 1, оставаясь
больше 1).
Опираясь на полученные данные, сделаем эскиз графика
(рис. 5).
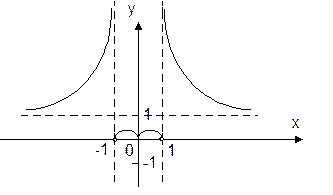
Рис. 5
5. Бесконечно малые величины и их сравнение
Функция 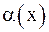 называется бесконечно малой величиной (б.м.в.) при
называется бесконечно малой величиной (б.м.в.) при 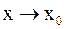 , если
, если 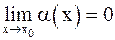 . Пусть
. Пусть 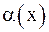 ,
, 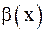 – б.м.в. при
– б.м.в. при 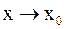 и
и 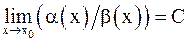 ; тогда
; тогда
а) если 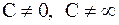 , то говорят, что
, то говорят, что 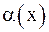 и
и 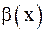 являются б.м.в. одного порядка;
являются б.м.в. одного порядка;
при С = 1 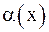 и
и 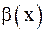 называются эквивалентными б.м.в. и при этом пишут
называются эквивалентными б.м.в. и при этом пишут 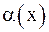 ~
~ 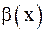 ;
;
б) если С = 0, то 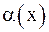 называется б.м.в. более высокого порядка чем
называется б.м.в. более высокого порядка чем 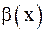 , и пишут
, и пишут 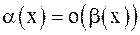 .
.
При 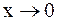 справедливы следующие соотношения, вытекающие из первого и второго замечательных пределов и непрерывности элементарных функций:
справедливы следующие соотношения, вытекающие из первого и второго замечательных пределов и непрерывности элементарных функций:
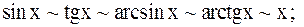
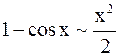 ,
, 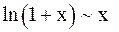 ,
, 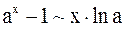 ;
;
 ,
, 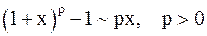 .
.
Эти соотношения используют для раскрытия неопределённостей.
Пример 11.Найти
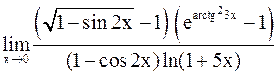 .
. 
Решение.Имеем
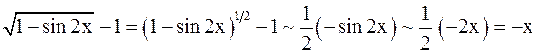 ,
,
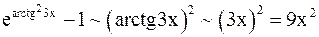 ,
,
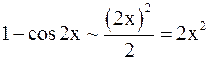 .
.
Учитывая это, получаем
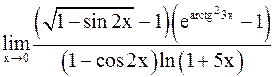 =
= 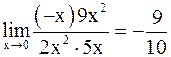 .
.
Пример 12. Найти
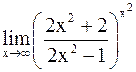 .
.
Решение.Имеем
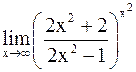 =
= 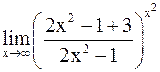 =
= 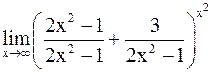 =
=
= 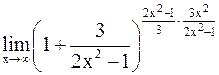 =
= 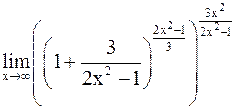 =
=
= 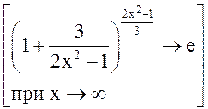 =
= 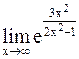 =
= 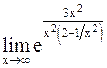 =
= 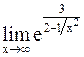 =
=  .
.
Пример 13. Найти предел
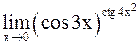 .
.
Решение.Имеем 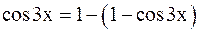 ~
~ 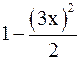 =
= 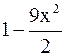 ,
,
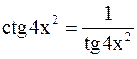 ~
~  . Отсюда находим
. Отсюда находим 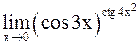 =
=
= 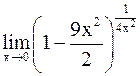 =
= 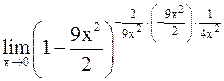 =
=
= 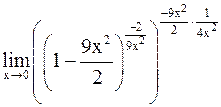 =
= 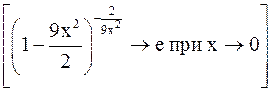 =
=
= 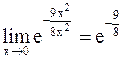 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Выбор аппаратуры управления и защиты электрооборудования | | | общих правил этикета. |
Дата добавления: 2019-02-07; просмотров: 571;
