Исследование математической модели
Алгоритм метода экспертных оценок включает следующие основные этапы (табл. 2):
1) определение нормированных оценок, данных экспертами:
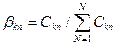
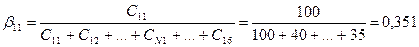
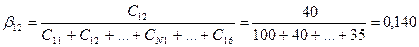
Таким же образом осуществляется нормирование оценок для остальных экспертов;
2) определение средних значений весовых коэффициентов для каждого вида оборудования:
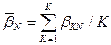
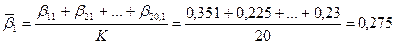

3) определение среднеквадратических отклонений весовых коэффициентов:
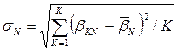

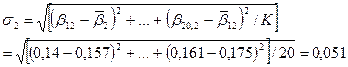
4) определение коэффициентов вариации:
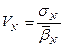
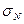 среднеквадратическое отклонение весовых коэффициентов
среднеквадратическое отклонение весовых коэффициентов
 среднее значение весовых коэффициентов
среднее значение весовых коэффициентов
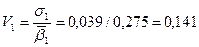
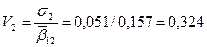
Значение расчетных параметров приведены в таблице 2.
5) переход от таблицы оценок в баллах к матрице рангов
В приведенной задаче важность разработки того или иного вида сменного оборудования оценивалась в баллах с помощью так называемой “шкалы отношений” (относительные, т. е. Сравнительные оценки, присуждаемыми экспертами) разным прогнозируемым направлениям). Удобна ли такая шкала оценок для экспертов и целесообразна ли вообще такая 100-бальная шкала? Установлено, что на практике повышенная точность 100- бальной шкалы оценок является кажущейся. Экспертам удобнее ранжировать направления, а не присваивать баллы. При переходе от таблицы оценок в баллах к матрице рангов виду рабочего сменного оборудования, имеющего наибольшею оценку в баллах 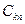 , присваивается первый номер (ранг)
, присваивается первый номер (ранг) 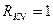 . Следующему по важности направлению присваивается ранг
. Следующему по важности направлению присваивается ранг 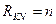 и т. д. До значения
и т. д. До значения  , (т. е. Оборудованию с наименьшей оценкой - последний). Оборудованию, имеющему одинаковые оценки, назначается одинаковый ранг. Ранговая шкала удобна также для “последующего определения” весовых коэффициентов (по важности направлений исследований, перспективности технических решений и т. д.). Весовые коэффициенты указывают на сравнительную значимость каждого события или объекта по отношению к аналогичным событиям или объектам. Причем для удобства сравнения весовые коэффициенты нормируются, т.е. вся совокупность их численных величин для всех рассматриваемых событий должна быть равна единице:
, (т. е. Оборудованию с наименьшей оценкой - последний). Оборудованию, имеющему одинаковые оценки, назначается одинаковый ранг. Ранговая шкала удобна также для “последующего определения” весовых коэффициентов (по важности направлений исследований, перспективности технических решений и т. д.). Весовые коэффициенты указывают на сравнительную значимость каждого события или объекта по отношению к аналогичным событиям или объектам. Причем для удобства сравнения весовые коэффициенты нормируются, т.е. вся совокупность их численных величин для всех рассматриваемых событий должна быть равна единице:
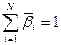
где 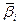 – весовой коэффициент; n-число ранжированных событий).
– весовой коэффициент; n-число ранжированных событий).
В соответствии с табл.1 проведем ранжирование видов рабочего сменного оборудования исходя из важности его разработки. Так, для первого вида оборудования (см. табл. 1) вместо баллов могут быть представлены ранги (табл.3). При этом возможны 2 случая:
a) Если сумма определенных рангов совпадает с суммой натурального ряда числе, то определенные величины рангов изменению не подлежат. В данной задаче для первого эксперта сумма рангов совпадает с суммой натурального ряда чисел, следовательно, ряд заносится в табл. 3 без изменений. 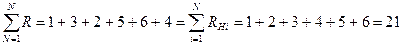 сумма натурального ряда чисел
сумма натурального ряда чисел
b) Если сумма определенных рангов не совпадает с суммой натурального ряда чисел, то одинаковым оценкам присваивается одинаковый ранг, равный среднему арифметическому соответствующих чисел натурального ряда.
Так, у 2 – го эксперта 1 – й вид и 3 – й вид оборудования оценены одинаково, по 100 баллов. В натуральном ряде чисел это будет соответствовать числам 1 и 2. Следовательно, первому и третьему виду оборудования должен быть назначен одинаковый ранг, который равен:

Матрица рангов, в которой сумма рангов каждого эксперта равна сумме натурального ряда чисел, называется нормированной.
Сумма натурального ряда чисел определяется по формуле:
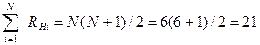
6) Определение суммы совпавших рангов для каждого эксперта:
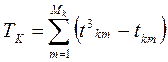
где 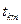 – число одинаковых рангов m-го типа в оценках К-го эксперта;
– число одинаковых рангов m-го типа в оценках К-го эксперта;
 - число видов сменного оборудования с совпавшими рангами в оценках К – го эксперта.
- число видов сменного оборудования с совпавшими рангами в оценках К – го эксперта.
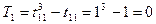
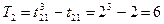
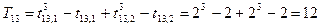
7) Определение общей суммы совпавших рангов:
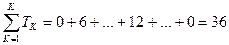
8) Определение суммы рангов для каждого вида сменного оборудования:
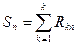
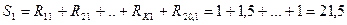

9) Определение средних значений сумм рангов по всем видам сменного оборудования:
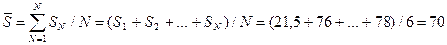
10) Вычисление квадратичных отклонений сумм рангов от их среднего значения:
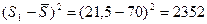
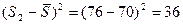
11) Определение суммы квадратичных отклонений:
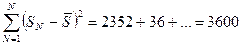
12) Определение коэффициента конкордации:
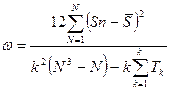 =
= 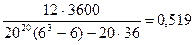
13) Определение величины критерия Пирсона:
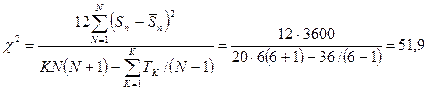
14) Определение числа степеней свободы:
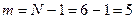
15) Определение табличного значения критерия Пирсона для заданного числа степенейсвободы m = 5 и 5% уровне значимости:
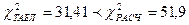
т.е. вероятность случайного совпадения мнений экспертов мала.
Если в процессе ранжировки для каждого эксперта использовать на каждый вид оборудования только числа натурального ряда без учета совпадения оценок по тому или иному виду оборудования (табл.4), то можно пользоваться упрощенной формулой для определения коэффициента конкордации:
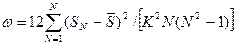
Сумма рангов для каждого вида сменного оборудования составит:
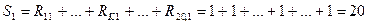

Среднее значение сумм рангов по всем видам сменного оборудования будет равно:
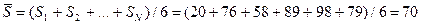
Квадратичные отклонения сумм рангов от их среднего значения составят:
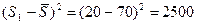
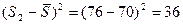
Сумма квадратичных отклонений будет равна:
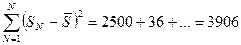
Коэффициент конкордации определяется по упрощенной формуле:

Расчетное значение критерия  определяется по формуле:
определяется по формуле:
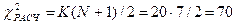
Среднее значение сумм рангов определяется по более простой формуле:
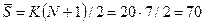
Табличное значение критерия 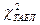 для 5%-го уровня значимости при числе степеней свободы m = N –1 = 6 – 1 = 5, будет равно:
для 5%-го уровня значимости при числе степеней свободы m = N –1 = 6 – 1 = 5, будет равно:
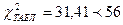
Табличное значение критерия Пирсона меньше расчетного.
т.е. гипотезу о наличии согласия экспертов при ранжировании вариантов принимаем.
Метод экспертных оценок позволяет эффективно использовать опыт специалистов, что сокращает время и стоимость выработки прогнозируемых решений, особенно на начальных этапах.
Коэффициент конкордации лежит в диапазоне 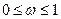 , причем
, причем 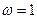 – полная согласованность мнений всех экспертов,
– полная согласованность мнений всех экспертов, 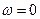 - полное несогласие экспертов в оценке события. Считают, что при
- полное несогласие экспертов в оценке события. Считают, что при  согласованность экспертов плохая;
согласованность экспертов плохая;
при 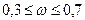 – средняя;
– средняя;
при 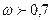 – высокая.
– высокая.
Вычисление коэффициента конкордации позволяет оценить степень достоверности экспертных результатов.
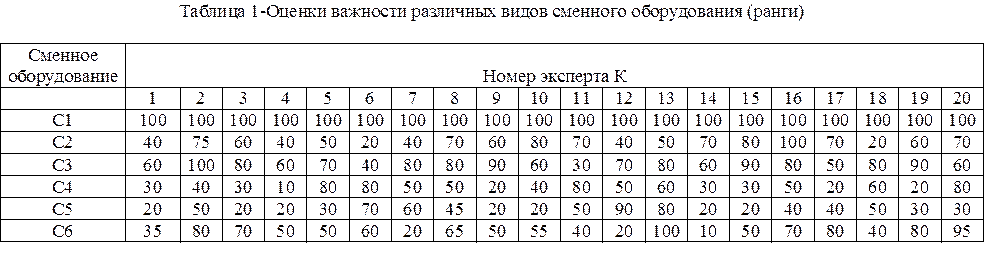
Дата добавления: 2017-03-29; просмотров: 416;
