Математическая модель задачи.
Задан график маршрутов G (гэ). Узлы графика нумеруются
1, 2,…, j,…n
Требуется найти такую совокупность стрелок графика G, при которой достигается минимум 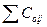 .
.
Возможность работы на объекте j0 только одним краном приписывается условием:
– промежуточное событие j0 может иметь не более чем одну входящую и выходящую стрелку;
– каждый исходный кружок может иметь одну выходящую, а завершающий – одну входящую стрелку.
Последовательность перехода машины i0 с объекта на объект выражает условие непрерывности работы кранов.
Решение задачи.
Для решения применяется вычислительная схема метода последовательных расчетов.
Графики маршрутов работы каждой группы кранов разбивают по времени на отдельные этапы, границами которых являются объекты-узлы.
В примере число таких этапов L равно 3.
На каждом этапе заканчиваются работы на одном или нескольких (S) объектах.
В последний этап расчетов необходимо включать монтажные работы на объектах которые начинаются в планируемом периоде, а заканчиваются в данном или последующем планируемом периоде.
Так, в расчет вводятся работы на объекте 5, а работы на объектах 1, 3, 6 и 10 не вводятся, т. к. они были учтены при расчете плана предыдущего периода.
Разнообразным вариантам маршрутов кранов ( К вариантов) на каждом этапе соответствует столько же вариантов суммарной себестоимости работ на объектах этапа.
В примере на 1 – м этапе таких вариантов 2:
по 1 – му варианту – кран № 3 выполняет работы на объекте 7, кран № 4 работает на объекте 11, суммарная себестоимость
5,4 + 8,1 = 13,5 усл. ед.;
по 2 – му варианту – кран № 3 работает на объекте 11, кран № 4 – на объекте 7, что дает суммарную себестоимость
5,6 + 8,1 = 13,7 усл. ед.;
В общем случае себестоимость производства монтажных работ по k – му (k = 1, 2,…,К) варианту на первом этапе равна:
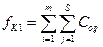
где S – число объектов, заканчивающихся на данном этапе,
m – число кранов
i – й кран, j – й объект
На следующем этапе каждому варианту будут соответствовать новые варианты производства работ и продолжения маршрутов 1 – го этапа.
Суммарная себестоимость по каждому варианту на 2 – м этапе складывается из себестоимости монтажных работ на данном этапе и величины fK на предыдущем этапе
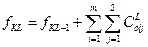
Среди всех вариантов суммарной себестоимости монтажа на всех объектах выбирается наименьшая величина (fKL), которая соответствует оптимальному решению задачи.
Расчеты удобно производить в табличном виде (табл.) с 10
В таблице производят поэтапное суммирование себестоимости по всем вариантам.
В графе “Себестоимость работ” и fK1 записаны соответственно составляющие суммарного размера и суммарная себестоимость по 2 – м возможным вариантам маршрутов работы кранов № 3 и 4.
Маршруты работы по 1 – му варианту 1 – го этапа с величиной f11 = 13,5 усл. ед. имеют на втором этапе 2 возможных продолжения:
1) кран № 2 работает на объекте 4, кран № 3 – на объекте 8;
2) кран № 2 работает на 8 – м объекте, кран № 3 –на объекте 4;
(работа кранов № 1 и 4 планируется на объектах 3 – го этапа).
Таблица – сравнение маршрутов работы кранов.
| Этап 1 | Этап 2 | Этап 3 | |||
| Себестоимость работ, усл. ед. | fK1 | Себестоимость работ, усл. ед. | fK2 | Себестоимость работ, усл. ед. | fK3 |
| 5,473 + 8,1114 5,6113 + 8,174 | 13,5 13,7 | 5,642 + 6,483=12 6,182 + 5,743=11,8 5,642 + 6,683=12,2 | 25,5 25,3 25,9 | 6,621 + 7,052 + 5,4123 + 6,994 6,991 + 5,822 + 7,653 + 7,2124 6,621 + 5,4122 + 6,953 + 6,994 6.991 + 7,3 52 + 5,623 + 7,2124 6,991 + 5,822 + 7,653 + 7,2124 | 51,4 51,1 52,3 53,2 |
Второй вариант 1 – го этапа имеет одно возможное продолжение маршрутов.
В графе “Себестоимость работ” 2 – го этапа по 3 – м вариантам записана себестоимость производства работ кранами на объектах этапа 2, а в графе fK2 записана сумма значений себестоимости на этапе 2 и величин fK1 этапа 1.
Себестоимость монтажа по оптимальному варианту составляет 51,1 усл. д. ед.
Направляясь от этой величины по строкам таблицы от 3 – го этапа к 1 – му, находят оптимальные маршруты каждого крана:
Кран № 1 выполняет работы на объектах 1, 2;
Кран № 2 – на объектах 3, 8 и 12;
Кран № 3 – на объектах 7, 4 и 5;
Кран № 4 – на объектах 11 и 9.
При анализе вариантов на всех этапах, начиная с 1 – го, необходимо отбраковать неоптимальные.
Порядок отбраковки следующий.
Находят суммарную себестоимость механизированных работ Сэт (эталонная) на последнем этапе по одному из вариантов, который принимают за эталонный.
Рассматривается другой вариант расстановки машин на 1 – м этапе графика маршрутов.
К себестоимости работ С на всех объектах первого этапа по этому варианту прибавляют наименьшую себестоимость работ на всех объектах остальных этапов без учета маршрута перебазировок машин, т. е. нижний предел себестоимости Сп .
Величина Сп является постоянной, для ее определения нужно на графике маршрутов для каждого объекта найти наименьшую себестоимость работ и составить сумму этих значений. Если сумма С + Сп ≥ Сэт , то сравниваемый второй вариант рассматривать не следует.
Дата добавления: 2017-03-29; просмотров: 412;
