Часто встречающиеся распределения дискретной случайной величины.
1. Закон распределения Бернулли. Пусть случайная величина 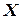 это число, характеризующее наступления события Aпри одном испытании. При этом множество возможных значений
это число, характеризующее наступления события Aпри одном испытании. При этом множество возможных значений 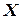 состоит из 2-х чисел 0 и 1:
состоит из 2-х чисел 0 и 1: 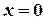 , если событие A не произошло, и
, если событие A не произошло, и 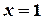 если событие A произошло. Таким образом:
если событие A произошло. Таким образом: 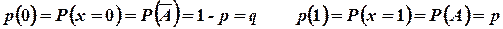
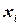
| 
| 
| |
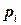
| 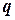
| 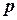
|
Распределение Бернулли играет фундаментальную роль в теории вероятностей и математической статистики, являясь математической моделью опыта с двумя исходами.
Пусть, например, имеется партия некоторой продукции, в которой продукция без дефектов встречается с вероятностью 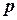 , а некачественная продукция с вероятностью
, а некачественная продукция с вероятностью 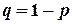 . Пусть случайная величина
. Пусть случайная величина 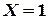 , если при выборе попалась качественная продукция и
, если при выборе попалась качественная продукция и 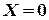 , если некачественная. Тогда случайная величина
, если некачественная. Тогда случайная величина 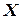 будет иметь распределение Бернулли.
будет иметь распределение Бернулли.
Пример 3.2. Случайная величина 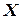 — число очков, выпадающих при однократном бросании игральной кости. Возможные значения
— число очков, выпадающих при однократном бросании игральной кости. Возможные значения 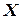 — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что
— числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что 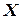 примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения?
примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения?
Решение: Здесь закон распределения вероятностей есть функция р(х)=1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.
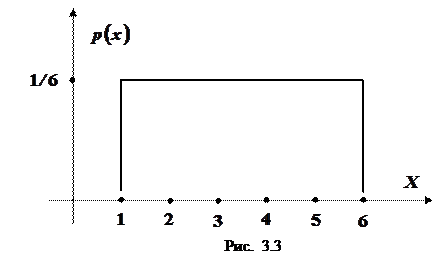 |
График этого закона имеет вид, изображенный на рис. 3.3.
2. Биноминальный закон распределения. Случайная величина 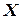 принимает значения:
принимает значения: 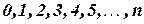 , с вероятностью, определяемой по формуле Бернулли:
, с вероятностью, определяемой по формуле Бернулли: 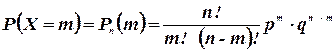 . Здесь
. Здесь 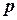 - постоянная вероятность того, что случайная величина
- постоянная вероятность того, что случайная величина 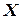 в серии
в серии 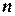 испытаний появится
испытаний появится 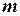 раз.
раз.
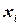
| 
| 
| 
| 
| 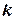
| 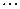
| 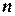
|
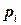
| 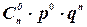
| 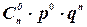
| 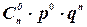
| 
| 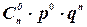
| 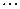
| 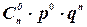
|
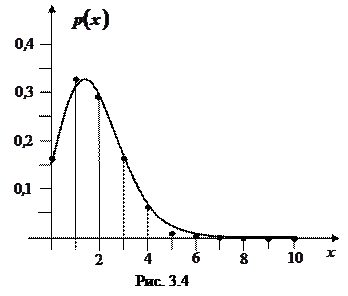
Пример этого закона мы рассмотрели выше. График этого закона имеет вид, изображенный на рис. 3.4.
3. Закон распределения Пуассона. Случайная величина 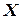 принимает бесконечное счетное число значений:
принимает бесконечное счетное число значений: 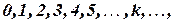 с вероятностью, определяющейся по формуле Пуассона:
с вероятностью, определяющейся по формуле Пуассона:
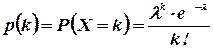 (3.2)
(3.2)
где 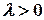 — некоторая положительная постоянная - параметр распределения Пуассона..
— некоторая положительная постоянная - параметр распределения Пуассона..
В этом случае говорят, что случайная величина 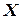 распределена по закону Пуассона. Заметим, что при
распределена по закону Пуассона. Заметим, что при 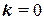 следует положить
следует положить 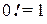 .
.
Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности 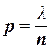 .
.
Пример 18. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?
Решение: Здесь 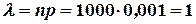 . По формуле (17) находим
. По формуле (17) находим
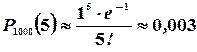
Распределение Пуассона часто встречается и в других задачах. Так, например, если телефонистка в среднем за один час получает N вызовов, то, как можно показать, вероятность 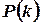 того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить
того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить 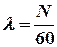 .
.
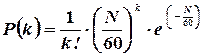
3. Функция распределения вероятностей случайной величины и ее свойства.
Рассмотрим некоторую функцию F(х), определенную на всей числовой оси следующим образом: для каждого х значение этой функции F(х) равно вероятности того, что дискретная случайная величина 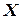 примет значение, меньшее х, т. е.
примет значение, меньшее х, т. е.
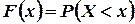 (3.3)
(3.3)
В этом случае эта функция называется функцией распределения вероятностей, или кратко, функцией распределения.
Пример 19. Найти функцию распределения случайной величины 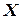 , приведенной в примере 17 (Случайная величина
, приведенной в примере 17 (Случайная величина 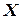 — число очков, выпадающих при однократном бросании игральной кости).
— число очков, выпадающих при однократном бросании игральной кости).
Решение: Ясно, что если 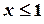 , то F(x)=0, так как
, то F(x)=0, так как 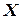 не принимает значений, меньших единицы.
не принимает значений, меньших единицы.
Если 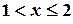 , то
, то 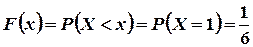 .
.
Если 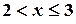 , то
, то 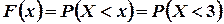 . Но событие
. Но событие 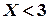 в данном случае является суммой двух несовместных событий:
в данном случае является суммой двух несовместных событий: 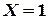 и
и 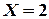 . Следовательно,
. Следовательно,
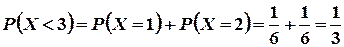
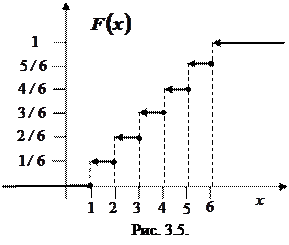 Итак, для
Итак, для 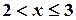 имеем F(x)=1/3. Аналогично вычисляются значения функции в промежутках
имеем F(x)=1/3. Аналогично вычисляются значения функции в промежутках 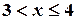 ,
, 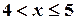 и
и 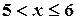 . Наконец, если
. Наконец, если 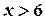 то F(x)=1, так как в этом случае любое возможное значение
то F(x)=1, так как в этом случае любое возможное значение 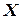 (1, 2, 3, 4, 5, 6) меньше, чем x. График функции F(x) изображен на рис. 3.5.
(1, 2, 3, 4, 5, 6) меньше, чем x. График функции F(x) изображен на рис. 3.5.
Зная функцию распределения F(x), легко найти вероятность того, что случайная величина 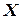 удовлетворяет неравенствам
удовлетворяет неравенствам 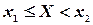 .
.
Действительно, рассмотрим событие, заключающееся в том, что случайная величина примет значение меньшее 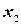 . Это событие распадается на сумму двух несовместных событий: 1) случайная величина
. Это событие распадается на сумму двух несовместных событий: 1) случайная величина 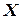 принимает значения, меньшие
принимает значения, меньшие 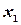 , т.е.
, т.е. 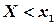 ; 2) случайная величина
; 2) случайная величина 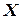 принимает значения, удовлетворяющие неравенствам
принимает значения, удовлетворяющие неравенствам 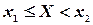 . Используя аксиому сложения, получаем:
. Используя аксиому сложения, получаем:
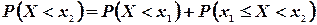 .
.
Отсюда 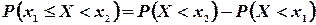 . Но по определению функции распределения F(x) [см. формулу (3.3)], имеем
. Но по определению функции распределения F(x) [см. формулу (3.3)], имеем 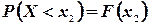 ,
, 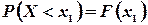 ; следовательно,
; следовательно,
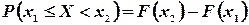 (3.4)
(3.4)
Таким образом, вероятность попадания дискретной случайной величины в интервал 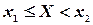 равна приращению функции распределения на этом интервале.
равна приращению функции распределения на этом интервале.
Рассмотрим основные свойства функции распределения.
1°. Функция распределения является неубывающей.
В самом деле, пусть 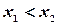 . Так как вероятность любого события неотрицательна, то
. Так как вероятность любого события неотрицательна, то 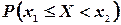 . Поэтому из формулы (3.4) следует, что
. Поэтому из формулы (3.4) следует, что 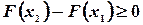 , т.е.
, т.е. 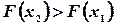 .
.
2°. Значения функции распределения удовлетворяют неравенствам 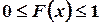 .
.
Это свойство вытекает из того, что F(x) определяется как вероятность [см. формулу (3.3)]. Ясно, что
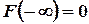 и
и 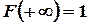 .
.
Здесь и в дальнейшем введены обозначения: 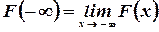 ,
, 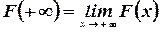 .
.
3°. Вероятность того, что дискретная случайная величина 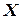 примет одно из возможных значений
примет одно из возможных значений 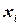 , равна скачку функции распределения в точке
, равна скачку функции распределения в точке 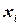 .
.
Действительно, пусть 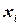 - значение, принимаемое дискретной случайной величиной, и
- значение, принимаемое дискретной случайной величиной, и 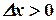 . Полагая в формуле (3.4)
. Полагая в формуле (3.4) 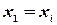 ,
, 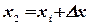 , получим
, получим
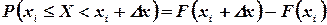
В пределе при 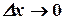 вместо вероятности попадания случайной величины на интервал
вместо вероятности попадания случайной величины на интервал 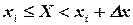 получим вероятность того, что величина
получим вероятность того, что величина 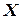 примет данное значение
примет данное значение 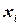 :
:
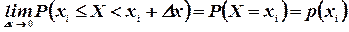
C другой стороны, получаем 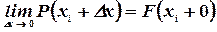 , т.е. предел функции F(x) справа, так как
, т.е. предел функции F(x) справа, так как 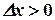 . Следовательно, в пределе формула примет вид
. Следовательно, в пределе формула примет вид
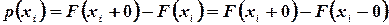
т.е. значение 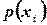 равно скачку функции
равно скачку функции 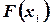 . Можно показать, что
. Можно показать, что 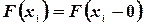 , т.е. что функция F(x) непрерывна слева в точке
, т.е. что функция F(x) непрерывна слева в точке 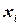 . Это свойство наглядно иллюстрируется на рис.4.
. Это свойство наглядно иллюстрируется на рис.4.
Дата добавления: 2018-11-25; просмотров: 522;
