Теплоотдача при вынужденном движении жидкости

Теплоотдача при движении жидкости вдоль плоской поверхности.

Если плоская поверхность пластины омывается потоком с равномерным распределением скоростей, то, начиная от передней кромки пластины, на ней образуется гидродинамический пограничный слой. В нем вследствие трения скорость жидкости изменяется от скорости, равной скорости невозмущенного потока, до нуля. Течение жидкости в пограничном слое может быть как ламинар­ным, так и турбулентным.

Опыты показывают, что переход от ламинарного режима течения к турбулентному происходит не мгновенно, а постепенно на некотором участке, течение на котором называется переходным.

О режиме течения в пограничном слое судят по величине числа Рейнольдса. Так, ламинарный режим течения в пограничном слое имеет место при Re_ж,l < 3×10⁵ и разрушение ламинарного слоя зависит от степени турбулентности набегающего потока. При наличии разности температур между потоком жидкости и пластиной у поверхности по­следней кроме гидродинамического образуется также и тепловой погра­ничный слой. В пределах теплового пограничного слоя температура жидкости изменяется от температуры потока вдали от пластины до температуры, равной температуре поверхности пластины.

Анализ опытных данных показывает, что коэффициент теплоотдачи зависит не только от изменения характера течения жидкости (лами­нарного или турбулентного), но и от рода жидкости, ее температуры, температурного напора и направления теплового потока, являющихся функцией температуры. Особенное значение имеет изменение вязкости жидкости в пограничном слое. При малых скоростях те­чения жидкости большое влияние на теплоотдачу оказывает естествен­ная конвекция.

Для определения среднего коэффициента теплоотдачи пластины, омываемой продольным потоком жидкости при ламинарном режиме в погранич­ном слое, можно рекомендовать следующую приближенную формулу при значениях чисел Re_ж,l < 3×10⁵:

Nu_ж,l = 0,664·Re_ж,l ^0,5·Pr_ж^0,33 ·e_t.

Здесь за определяющую температуру принята тем­пература набегающего потока; за определяющую скорость – скорость набегающего потока; за опре­деляющий размер – длина пластины по направлению потока.

При турбулентном гидродинамическом пограничном слое у поверх­ности пластины образуется тонкий слой ламинарно текущей жидкости, называемый ламинарным подслоем, в котором происходит основное изменение скорости потока. Также в ламинарном подслое происходят почти все изменение температуры текущей жидкости, т. е. ламинарный подслой представляет главное гидродинамическое и термическое со­противление.

Для определения сред­него коэффициента теплоотдачи при турбулент­ном пограничном слое (Re_ж,l > 3×10⁵) рекомен­дуется уравнение:

Nu_ж,l = 0,037·Re_ж,l ^0,8·Pr_ж^0,4 ·e_t.

Теплоотдача при вынужденном течении жидкости в трубах.

Механизм процесса теплоотдачи при течении жидкости в прямых гладких трубах является очень сложным. Интенсивность теплообмена может изменяться в широких пределах и в большей степени зависит от скорости движения потока.

Изменение температуры жидкости происходит как по сечению, так и по длине трубы.

Характер движения жидкости в трубах может быть ламинарным, переходным и турбулентным. О режиме течения судят по величине числа Рейнольдса: Re = wd/n,где w – средняя скорость жидкости; d – внутренний диаметр трубы; n – кинематический коэффициент вязкости. При Re £ 2300 – ламинар­ный режим; при Re ³ 10⁴ – турбу­лентный режим; при 2300 < Re < 10⁴ переходный режим. Формирова­ние характера потока происходит в на­чальном участке трубы. При входе в трубу скорости по сечению распределяются равномерно. В дальнейшем при течении вдоль трубы у стенок образуется гидродинамический пограничный слой, толщина которого постепенно увеличивается и становится равной радиусу трубы, а в трубе устанавливается по­стоянное распределение скоростей, характерное для данного режима течения, или наступает так называемое, стабилизованное течение. Длина участка стабилизации равна примерно 50×d.

Теория и опыты показывают, что теплоотдача при течении жидкости в трубе неодинакова по длине и поэтому кроме участка стабилизован­ного течения образуется участок, тепловой стабилизации. У входа в трубу коэффициент теплоотдачи a имеет максимальное зна­чение, а затем резко убывает и при стабилизованном течении стремится к неизменному значению.

При ламинарном течении жидкости встречаются два режима движения: вязкостный и вязкостно-гравитационный.

Вязкостныйрежим соответствует течению вязких жидкостей при отсутствии естественной конвекции. При этом режиме передача тепло­ты к стенкам канала (и наоборот) осуществляется только теплопро­водностью.

Вязкостно-гравитационный режим имеет место тогда, когда вы­нужденное течение жидкости сопровождается и естественной конвек­цией. При этом режиме, теплота будет передаваться не только тепло­проводностью, но и конвекцией.

При турбулентном движении жидкости, в связи с более сложным строением потока, распределение скоростей описать одним уравнением не удается. Почти все сечение трубы заполнено турбулентным потоком и только у самой стенки образуется ламинарный подслой, представ­ляющий основное термическое сопротивление.Наиболее резко ско­рость потока изменяется вблизи стенки трубы в пределах пограничного слоя. Максимальная скорость потока наблюдается на оси трубы. В практических расчетах пользуют­ся средними скоростями w = V/F,

где V – объемный расход жидкости, м³/с; F – площадь поперечного сечения трубы, м².

При турбулентном потоке жидкость интенсивно перемеши­вается и естественная конвекция практически не оказывает влияния на теплоотдачу. Температура жидкости по се­чению ядра практически постоянна.

При нагревании жидкости интенсивность теплоотдачи выше, чем при охлаждении.

Для расчета среднего коэффициента теплоотдачи рекомендованы следующие критериальные уравнения:

ламинарное течение

вязкостный режим Nu_ж,d = 0,15·Re_ж,d ^0,33·Pr_ж^0,43 ·e_t;

вязкостно-гравитационный режим Nu_ж,d = 0,15·Re_ж,d ^0,33·Pr_ж^0,43×Gr_ж,d ^0,1 ·e_t;

турбулентное течение

Nu_ж,d = 0,021·Re_ж,d ^0,8·Pr_ж^0,43 ·e_t.

За определяющую темпера­туру принята средняя температура жидкости; за определяющую скорость – средняя скорость жидкости в трубе; за определяющий размер – диаметр круглой трубы или эквивалентный диаметр трубы любой формы (d_экв = 4F/P, где P – внутренний периметр канала, м).

Эти формулы дают среднее значение a при l/d >50. Они применимы для любой жидкости. Для труб, имеющих длину l < 50×d,следует полученное значение a умножить на средний поправочный коэффициент e_l, величина которого приведена в таблице

При течении жидкости в изогнутых трубах ­– змеевиках – вследствие центробежного эффекта в поперечном сечении трубы возникает вторичная циркуляция, наличие которой приводит увеличению коэффициента теплоотдачи. Расчет теплоотдачи в зме­евиках следует вести по уравнениям для прямой трубы, но полученное значение a необходимо умножить на поправочный коэффициент e_зм = 1 + 1,77d/R, где R – радиус изгиба трубы.

В переходной зоне теплоотдачу рас­считывают по интерполяционному соотношению

Nu/Nu_т = g + (1 – g)Nu_л/Nu_т,

где Nu_л и Nu_т определяют по приведенным выше форму­лам для ламинарного и турбулентного течения; g – коэффициент перемежаемости g = 1 – exp(1 – Re/2300).

Шероховатость стенок при ламинарном режиме течения не сказывается на трении и теплоотдаче, если, конечно, высота неровностей d_ш мала по сравнению с радиусом трубы. При турбулентном режиме значение d_ш необходимо со­относить с толщиной вязкого подслоя d_в. Если d_ш << d_в, то стенка считается гидравлически гладкой. При d_ш << d_в вследствие вихреобразования на вершинах неровностей интенсивность турбулентности заметно увели­чивается, что ведет к росту теплоотдачи. Одна­ко при этом растет и гидравлическое сопротивление. Сле­довательно, вопрос о применении шероховатости для ин­тенсификации теплоотдачи должен решаться как некото­рая задача оптимизации.

Теплоотдача при поперечном омывании одиночной круглой трубы. Процесс теплоотдачи при поперечном потоке жидкости, омываю­щем круглую трубу, характеризуется рядом особенностей. Плавное, безотрывное омывание поверхности наблю­дается только при Re < 5. При больших значениях Re условия омывания лобовой и кормовой половин трубы различны. Ламинарный пограничный слой, образующийся в лобовой части трубы около вертикального диаметра, отрывается от ее поверхности, и в кормовой части образуются два симметричных вихря.

Только при углах j = 80 – 85°, считая от лобовой точки, поверхность трубы омывается по­током жидкости безотрывно, вся осталь­ная ее часть находится в вихревой зоне. Чем больше скорость потока, тем при больших углах j происходит отрыв ла­минарного пограничного слоя. При боль­ших значениях числа Re ламинарный пограничный слой переходит в турбу­лентный, а отрыв слоя происходит при j = 120 – 130°. Это смещение приводит к уменьшению вихревой зоны в кормо­вой части трубы и обтекание ее улуч­шается. Турбулентный пограничный слой появляется при числах Re = 1×10⁵ – 4×10⁵. На появление турбулентного пограничного слоя боль­шое влияние оказывает начальная турбу­лентность потока; чем она больше, тем при меньших значениях чис­ла Re появится турбулентный пограничный слой.

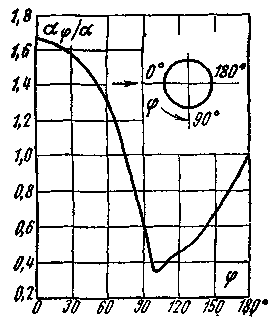
Такая картина движения .жидкости отражается на коэффициенте теплоотдачи по окружности трубы (см. рисунок). На рисунке a_j – местный коэффициент теплоотдачи, а a – средний коэффициент теплоотдачи.

В лобовой части трубы (при j = 0) коэффициент теплоотдачи имеет наибольшее значение, так как пограничный слой имеет наименьшую толщину. По мере движения жидкости вдоль поверхности толщина по­граничного слоя увеличивается и достигает максимального значения почти у экватора, что примерно соответствует месту отрыва пограничного слоя. Благодаря увеличению толщины пограничного слоя a_j уменьшается и у экватора достигает наименьшего значения. В кормовой части за счет вихреобразования происходит разрушение пограничного слоя, толщина его уменьшается, a_j увеличивается, достигая максимального значения при j = 180^о.

Для расчета среднего коэффициента теплоотдачи рекомендованы следующие критериальные уравнения:

при 5 < Re £ 10³ Nu_ж,d = 0,5·Re_ж,d ^0,5·Pr_ж^0,38 ·e_t;

при 10³ < Re £ 2×10⁵ Nu_ж,d = 0,25·Re_ж,d ^0,6·Pr_ж^0,38 ·e_t;

при Re = 3×10⁵ – 2×10⁶ Nu_ж,d = 0,023·Re_ж,d ^0,8·Pr_ж^0,37 ·e_t.

Здесь скорость потока отнесена к самому узкому поперечному сечению канала, где установлена труба. Как определяющая используется средняя температура жидкости, а определяющим размером служит наружный диаметр трубы. Уравнения справедливы для трубы расположенной перпендикулярно направлению потока (угол атаки b = 90^о) Если b < 90^о, то вводится в виде множителя поправочный коэффициент, выбираемый из справочника.

Теплоотдача при поперечном омывании пучков труб.

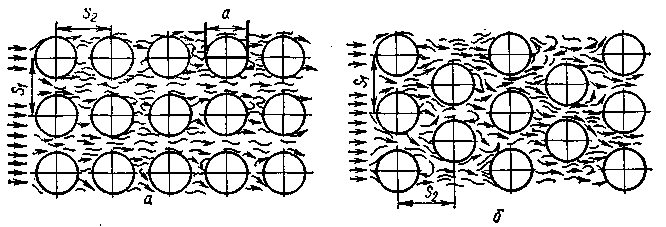
Теплообменные аппараты с одиночно располо­женной трубой в поперечном потоке жидкости применяют редко, чаще аппараты компонуют из трубных пучков. Наиболее распростра­нены в технике два типа трубных пучков: коридорные (рис. а) и шахматные (рис. б).

В трубных пучках трубы первого ряда находятся приблизитель­но в тех же условиях, что и одиночный цилиндр. На теплообмене второго и последующих рядов сказывается турбулизация потока, создаваемая первыми рядами, но эффект добавочной турбулизации постепенно ослабевает по мере увеличения числа предшествующих поперечных рядов. Экспериментально установлено, что, начиная с третьего ряда, поток практически стабилизирован, поэтому и сред­ний коэффициент теплоотдачи для всех последующих рядов можно считать постоянной величиной.

В коридорном пучке передние трубы закрывают задние, и между ними создается застойная зона с пониженной циркуляцией жидкости: a в лобовой части труб падает. В шахматном пучке все трубы находятся в одинаковых условиях и благодаря повышенной турбулизации потока a в шахматном пучке выше, чем в коридорном.

Коэффициент теплоотдачи первого ряда составляет приблизитель­но 60% значения a на стабилизированном участке (a =0,6a₃) как для коридорного, так и для шахматного пучков. Для второго ряда в коридорном пучке a₂ = 0,9a₃, а при шахматном расположении труб a₂ =0,7a₃.

На интенсивность теплообмена пучков влияет также плотность пучка, которую можно характеризовать соотношениями между по­перечным шагом S₁,продольным шагом S₂ и диаметром труб – d.

Средний коэффициент теплоотдачи для третьего и последующих рядов труб может быть вычислен по следующему уравнению:

Nu_ж,d = С·Re_ж,d ^п·Pr_ж^0,33 ·e_t·e_s·e_b,

где для шахматных пучков С = 0,41; п = 0,60; для коридорных пучков С = 0,26; п = 0,65. Поправочный коэффициент e_s учитывает влияние относительных шагов: для шахматного пучка при S₁/ S₂ < 2 e_s = (S₁/ S₂)^1/6; при S₁/ S₂ ³ 2e_s = l,12; для кори­дорного пучка e_s = (S₂/d)^-0,15. Поправка на угол атаки e_bдля пучков может быть определена по справочным данным.

Критериальное уравнение справедливо в интервале значений Re = 10³ – 10⁵. В качестве определяющего размера принят диаметр труб, в качестве характерной скорости – скорость в самом узком сече­нии потока в пучке. Определяющая температура – средняя температура жидкости.