Термодинамические процессы
Изохорный процесс, процесс, протекающий при постоянном объеме. Уравнение процесса v = const. Основные формулы для расчета изохорного процесса с идеальным газом:
| 1-2, 3-4 – изохорные процессы подвода теплоты
|
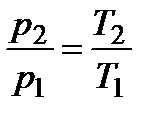 ;
; 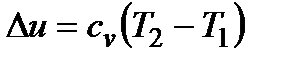 ;
; 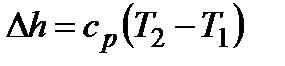 ;
; 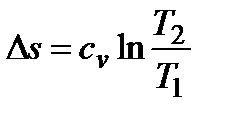 ; l = 0;
; l = 0; 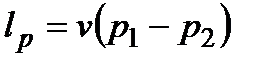 ;
; 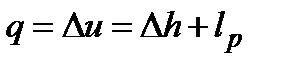
Изобарный процесс, процесс, протекающий при постоянном давлении. Уравнение процесса р = const. Основные формулы для расчета изобарного процесса с идеальным газом:
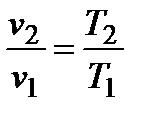 ;
; 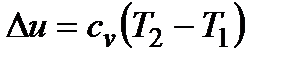 ;
; 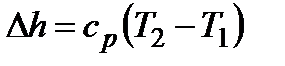 ;
; 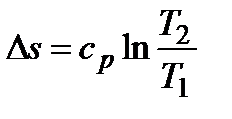 ;
; 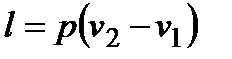 ; lp = 0;
; lp = 0; 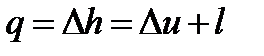
| 1-2, 3-4 – изобарные процессы подвода теплоты
|
Изотермический процесс, процесс, протекающий при постоянной температуре. Уравнение процесса Т = const. Основные формулы для расчета изотермического процесса с идеальным газом:
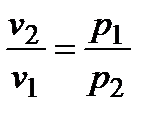 ;
; 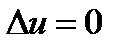 ;
; 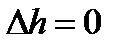 ;
; 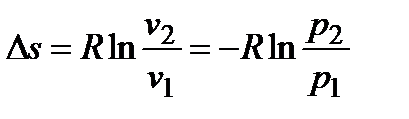 ;
; 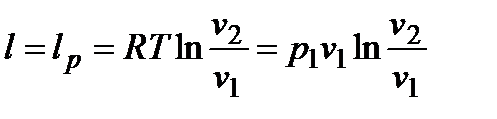 ;
; 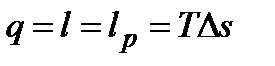
| 1-2, 3-4 – изотермические процессы подвода теплоты
|
Адиабатный процесс, процесс, протекающий без теплообмена с окружающей средой (q = 0, dq = 0). Равновесные адиабатные процессы протекают при постоянной энтропии (ds = 0, s = const). Уравнение адиабатного процесса 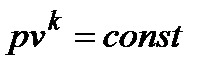 , где k – показатель адиабаты. Для идеального газа
, где k – показатель адиабаты. Для идеального газа 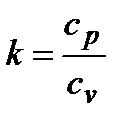 и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом:
и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом:
q = 0; s = const; 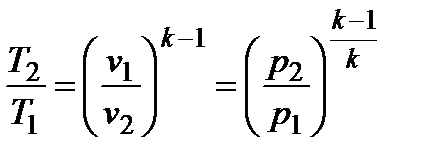 ;
; 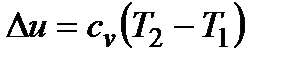 ;
; 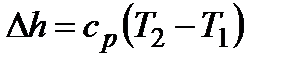 ;
; 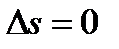 ;
;
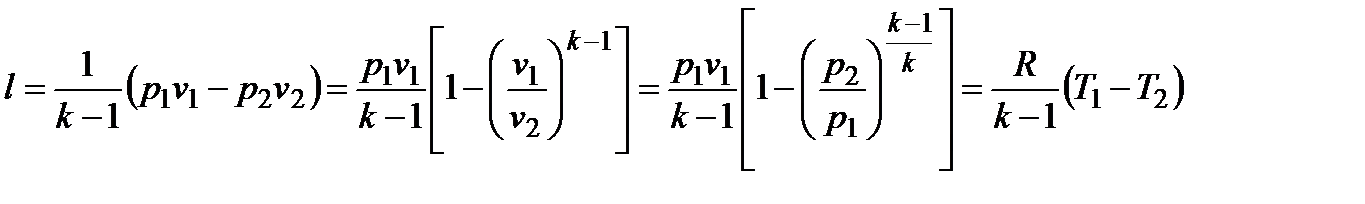 ;
; 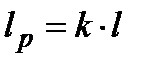 ; l = -Du; lp = -Dh = h1 – h2
; l = -Du; lp = -Dh = h1 – h2
Политропный процесс, процесс, протекающий с постоянной теплоемкостью сп = const. Уравнение политропного процесса 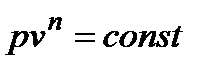 , где п – показатель политропы. Для идеального газа
, где п – показатель политропы. Для идеального газа 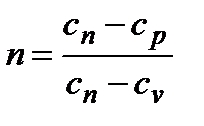 . Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом:
. Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом:
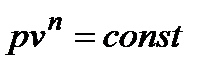 ;
; 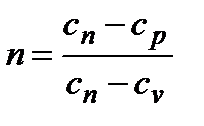 ;
; 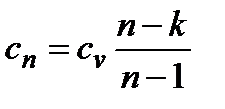 ;
; 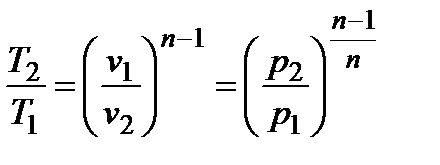 ;
; 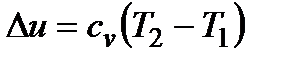 ;
;
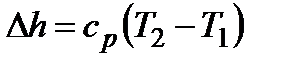 ;
; 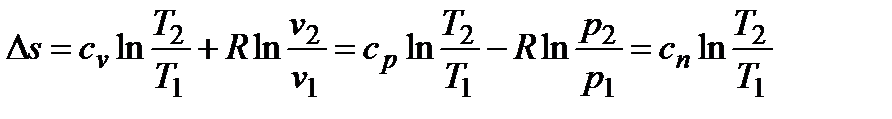 ;
;
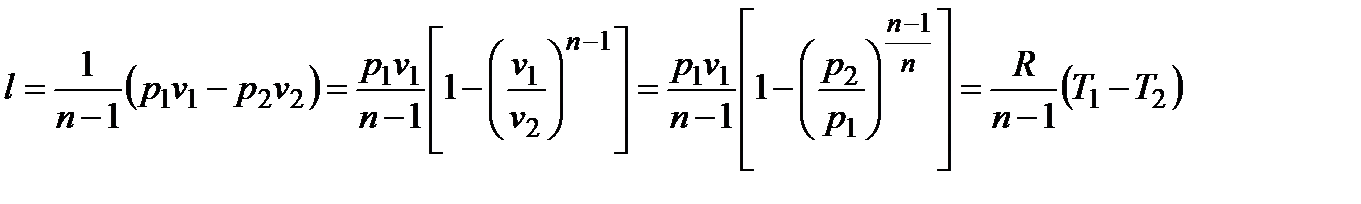 ;
; 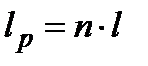 ;
; 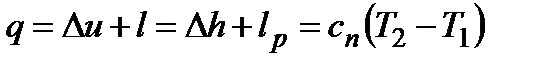
| Процесс
| п
| cn
|
| Изохорный
| ± ¥
| cv
|
| Изобарный
|
| cp
|
| Изотермический
|
| ¥
|
| Адиабатный
| k
|
|
Качественные особенности реальных газов. Исследования свойств реальных газов в широком диапазоне термодинамических параметров показали, что свойства таких газов отклоняются от законов, справедливых для идеальных газов, тем значительнее, чем выше их плотность. Молекулы реальных газов в отличие от идеальных газов имеют определенные (конечные) размеры, и между ними существуют силы межмолекулярного взаимодействия. При определенных условиях эти силы могут приводить к ассоциации или диссоциации молекул, что существенно отражается на свойствах газа. При малых межмолекулярных расстояниях внутренние силы могут действовать как силы отталкивания и создавать внутреннее давление. При значительных расстояниях между молекулами действуют главным образом силы взаимного притяжения. В связи с этим поведение термических и калорических свойств реальных газов значительно отличаются от идеальных. Например, коэффициент сжимаемости 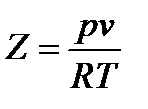 для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры.
для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры.
В отличие от теплоемкости идеальных газов теплоемкости ср и cv реальных газов зависят не только от температуры, но и от давления. Эти зависимости имеют сложный характер. В области низких давлений зависимости изохорной и изобарной теплоемкостей от температуры близки к линейным. При давлениях ниже критического теплоемкости ср и cv возрастают с понижением температуры и приближением к состоянию сжижения, что связано с процессом ассоциации молекул. В области высоких температур влияние температуры оказывается незначительным. Повышение давления в этой области приводит к увеличению теплоемкости. В области сверхкритических давлений изобары теплоемкости проходят через максимум, который с повышением давления смещается в сторону высоких температур. Величина ср (или cv)в точке максимума увеличивается с приближением к ркр (рис. 8.7, б). В критической точке изобарная теплоемкость равна бесконечности.
Уравнение состояния реальных газов. Для реальных газов предложено много уравнений состояния, но ни одно из них не обладает достаточной общностью и точностью.
Физические особенности реальных газов качественно хорошо отражаются уравнением Ван-дер-Ваальса. Оно же является и наиболее простым, единым для жидкой и газовой фаз, термическим уравнением состояния. Ван-дер-Ваальс учел влияние сил взаимодействия молекул и влияние их объема путем введения поправочных факторов в уравнение состояния идеального газа. Это уравнение, полученное на основе, главным образом, умозрительных качественных заключений имеет вид 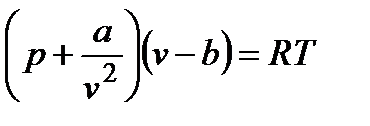 , где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует
, где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует 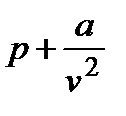 , а вместо v стоит
, а вместо v стоит 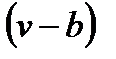 . Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член
. Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член 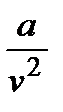 учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества
учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества 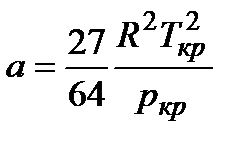 ,
, 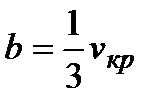 . В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно.
. В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно.
Гетерогенная система, система, состоящая из различных по своим свойствам частей, разграниченных поверхностями раздела (лед-вода, вода-пар).
Гомогенная система, система, между любыми частями которой нет поверхностей раздела (пар, вода, лед).
Фаза, гомогенная часть гетерогенной системы, ограниченная поверхностью раздела.
Фазовый переход, переход вещества из одного фазового состояния в другое.
Парообразование, переход вещества из жидкого состояния в газообразное (пар).
Испарение, парообразование, происходящее только на свободной поверхности жидкости при любой температуре.
Кипение, парообразование, происходящее во всем объеме жидкости в результате подвода теплоты при температуре кипения.
Конденсация, переход вещества из газообразного состояния в жидкое в результате отвода теплоты при температуре кипения.
Сублимация, переход вещества из твердого состояния в газообразное в результате подвода теплоты при температуре сублимации. Для воды этот процесс возможен при давлениях ниже давления в тройной точке (< 610,8 Па). Процесс перехода вещества из газообразного состояния в твердое, называют десублимацией.
Плавление, переход вещества из твердого состояния в жидкое в результате подвода теплоты при температуре плавления. Процесс перехода вещества из жидкого состояния в твердое, называют затвердеванием (кристаллизацией).
Температура фазового перехода, температура вещества в процессе равновесного фазового перехода при постоянном давлении.
Температура кипения (насыщения), температура вещества в процессе равновесного фазового перехода из жидкого состояния в газообразное (пар) при постоянном давлении. Обозначают tн или ts. При этой же температуре происходит конденсация.
Теплота фазового перехода, количество теплоты, которое необходимо подвести или отвести при равновесном изобарно-изотермическом переходе вещества из одной фазы в другую.
Теплота парообразования (удельная),теплота, затраченная на превращение 1 кг кипящей жидкости в сухой насыщенный пар при постоянном давлении. Обозначают r, Дж/кг.
Тройная точка, точка на термодинамической диаграмме, соответствующая состоянию, в котором находятся в равновесии три фазы вещества: твердая, жидкая, газообразная. Параметры состояния в тройной точке у различных веществ различны. Для воды: р0 = 610,8 Па, t0 = 0,01 оС, v0 = 0,001 м3/кг.
Критическая точка, точка на термодинамической диаграмме, в которой исчезает различие между жидкой и газообразной фазами. Состояние вещества в этом случае называют критическим состоянием. Параметры состояния в критической точке у различных веществ различны. Для воды: рк = 22,115 МПа, tк = 374,12 оС, vк = 3,147 м3/кг.
Насыщенный пар, пар, находящийся в равновесии с жидкой фазой.
| Рисунок – Фазовые pv-, Ts- и hs-диаграммы
|
Сухой насыщенный пар, пар, в котором при температуре кипения (насыщения) отсутствуют взвешенные частицы жидкой фазы.
Влажный насыщенный пар, насыщенный пар, в котором содержатся взвешенные частицы жидкой фазы.
Степень сухости пара, массовая доля сухого пара во влажном насыщенном паре. Обозначают х. Степень сухости может изменяться от 0 до 1. При х = 0 – кипящая жидкость, при х = 1 - сухой насыщенный пар.
Перегретый пар, пар, температура которого выше температуры кипения при одинаковом давлении.
| Рисунок - Фазовая pT-диаграмма
|
Фазовая диаграмма, диаграмма, на которой нанесены линии фазовых переходов. На рисунке представлена фазовая диаграмма в координатах р, Т. Линия ОВ - кривая сублимации (десублимации) вещества, линия ОА - кривая плавления (затвердевания), линия ОК - кривая насыщения (кипения или конденсации). Точка О - тройная точка. Точка К - критическая точка.
На практике чаще применяют фазовые диаграммы в координатах p,v, T,s, h,s (см. рисунок). На этих диаграммах представляют область некипящей жидкости (ж), влажного насыщенного пара (в.п) и перегретого пара (п.п). На линии, соответствующей степени сухости х = 0, находятся состояния кипящей жидкости. Эту линию называют нижней пограничной кривой. На линии, соответствующей степени сухости х = 1, находятся состояния сухого насыщенного пара. Эту линию называют верхней пограничной кривой.
Основные параметры воды, параметры, необходимые для проведения термодинамических расчетов: давление, температура, удельный объем, энтальпия, энтропия. Поскольку вода является реальным веществом, сведения о параметрах и функциях состояния получают экспериментальным путем, а затем представляют в виде таблиц, диаграмм (Ts-, hs-диаграммы) и уравнений состояния.
Начало отсчета энтальпии и энтропии воды - состояние в тройной точке (h0 = 0, s0 = 0). Параметры, относящиеся к состоянию кипящей жидкости, обозначают индексом «'», например, v', h', s'. Параметры, относящиеся к состоянию сухого насыщенного пара, обозначают индексом «"», например, v", h", s". Параметры влажного насыщенного пара определяют с помощью фазовых диаграмм, или рассчитывают по правилу аддитивности: v = v"x + v'(1 – x),
h = h"x + h'(1 – x) = h' + rx, s = s"x + s'(1 – x) = s' + rx/Tн.
При невысоких и средних давлениях (до 10 МПа), функции состояния можно определять расчетным путем (с достаточной для технических расчетов точностью). Необходимые формулы представлены в таблице, где cрж » 4,19 кДж/(кг×К) – изобарная теплоемкость жидкой воды; cрп - средняя изобарная теплоемкость перегретого пара в интервале температур от температуры кипения до данной температуры.
Таблица – Расчет функций состояния воды
| Состояние воды
| Энтальпия
| Энтропия
| Внутренняя
энергия
|
| Некипящая жидкость
| h = cрж×t
| 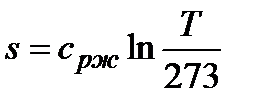
| u = h – pv
|
| Кипящая жидкость
| h' = cрж×tн
| 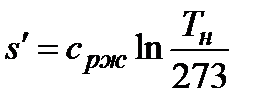
| u' = h' – pv'
|
| Сухой насыщенный пар
| h" = h' + r
| 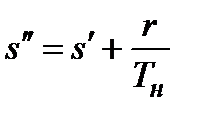
| u" = h" – pv"
|
| Перегретый пар
| 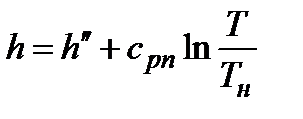
| 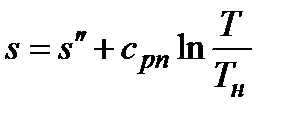
| u = h – pv
|
| Рисунок – Процесс получения пара в pv-, Ts- и hs-диаграммах
|
Процесс получения пара, процесс 1-2-3-4, представленный на рисунке и протекающий с подводом теплоты. В технических устройствах этот процесс рассматривают как изобарный, состоящий из трех частей: 1-2 - изобарный подогрев воды до температуры кипения; 2-3 - изобарно-изотермическое парообразование; 3-4 - изобарный перегрев пара.
Обратный процесс (4-3-2-1) протекает с отводом теплоты и заключается в изобарном охлаждении перегретого пара до температуры кипения (4-3), изобарно-изотермической конденсации (3-2) и изобарном охлаждении жидкости ниже температуры кипения (2-1).
Термодинамические процессы с водяным паром, изохорный, изобарный, изотермический и адиабатный процесс.
Изохорный процесс.
Процесс 1-2 – подвод теплоты.
Работа изменения объема: l = 0. Располагаемая работа: lp = v(p1 – p2).
Количество теплоты: q = Du = Dh + lp = (h2 – h1) + lp.
Изобарный процесс.
Процесс 1-2 – подвод теплоты.
Работа изменения объема: l = p(v2 – v1). Располагаемая работа: lp = 0.
Количество теплоты: q = Dh = h2 – h1 = Du + l.
Изотермический процесс.
1-2 – подвод теплоты.
Работа изменения объема: l = q – Du. Располагаемая работа: lp = q – Dh.
Количество теплоты: q = T(s2 – s1) = Du + l = Dh + lp.
Изменение внутренней энергии: Du = (h2 – h1) – (p2v2 – p1v1).
Адиабатный процесс.
Процесс 1-2 – расширение.
Работа изменения объема: l = -Du. Располагаемая работа: lp = -Dh = h1 – h2.
Количество теплоты: q = 0. Изменение внутренней энергии: Du = (h2 – h1) – (p2v2 – p1v1).
Уравнение Клапейрона-Клаузиуса, уравнение, устанавливающее связь между величинами, характеризующими процесс перехода вещества из одного агрегатного состояния в другое. Так для процесса парообразования (конденсации) уравнение Клапейрона-Клаузиуса имеет вид: 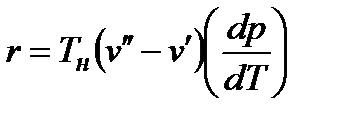 , где
, где 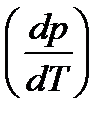 – наклон линии фазового перехода в координатах р, Т.
– наклон линии фазового перехода в координатах р, Т.
Дата добавления: 2018-11-25; просмотров: 813;
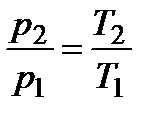 ;
; 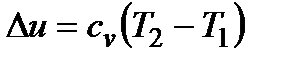 ;
; 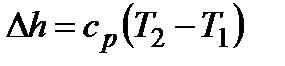 ;
; 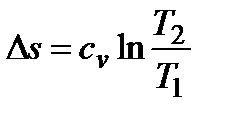 ; l = 0;
; l = 0; 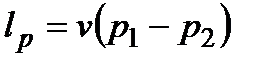 ;
; 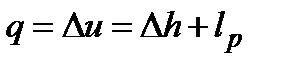
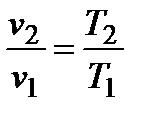 ;
; 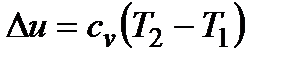 ;
; 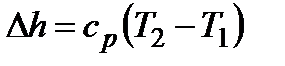 ;
; 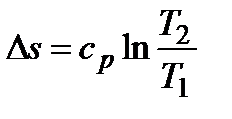 ;
; 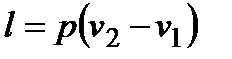 ; lp = 0;
; lp = 0; 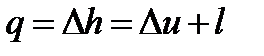
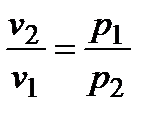 ;
; 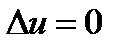 ;
; 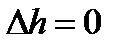 ;
; 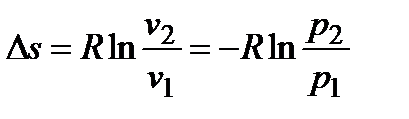 ;
; 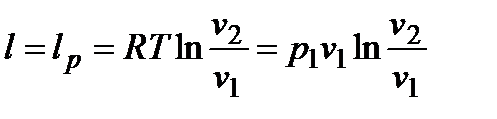 ;
; 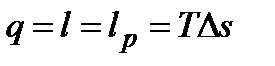
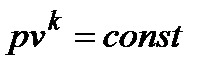 , где k – показатель адиабаты. Для идеального газа
, где k – показатель адиабаты. Для идеального газа 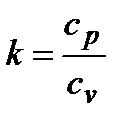 и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом:
и принимает следующие значения: для одноатомных газов k = 1,67, для двухатомных газов k = 1,4, для трёх- и многоатомных газов k = 1,29. Основные формулы для расчета адиабатного процесса с идеальным газом:
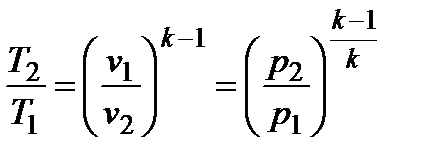 ;
; 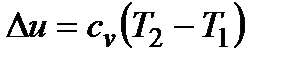 ;
; 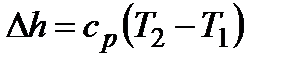 ;
; 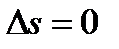 ;
;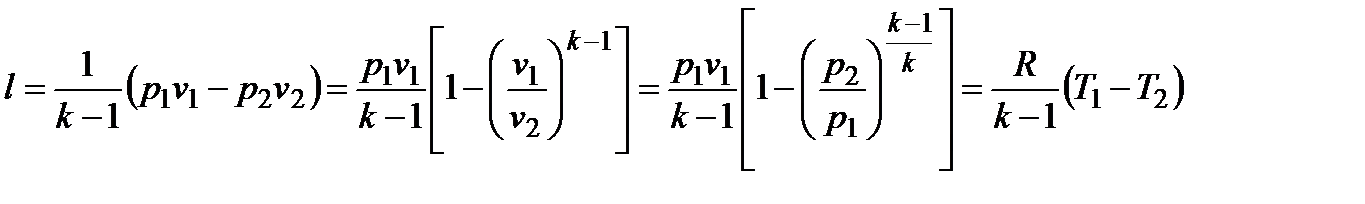 ;
; 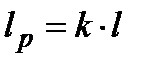 ; l = -Du; lp = -Dh = h1 – h2
; l = -Du; lp = -Dh = h1 – h2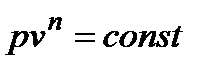 , где п – показатель политропы. Для идеального газа
, где п – показатель политропы. Для идеального газа 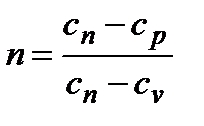 . Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом:
. Изохорный, изобарный, изотермический и адиабатный процесс являются частным случаем политропного процесса. Основные формулы для расчета политропного процесса с идеальным газом:
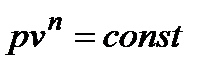 ;
; 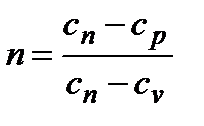 ;
; 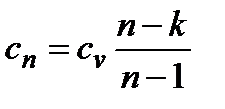 ;
; 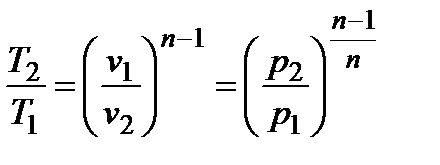 ;
; 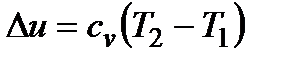 ;
;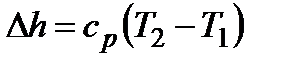 ;
; 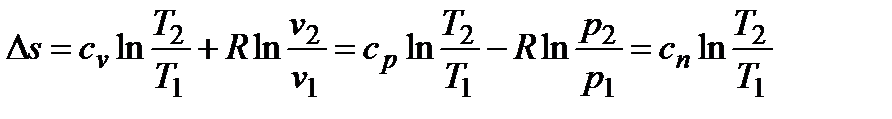 ;
;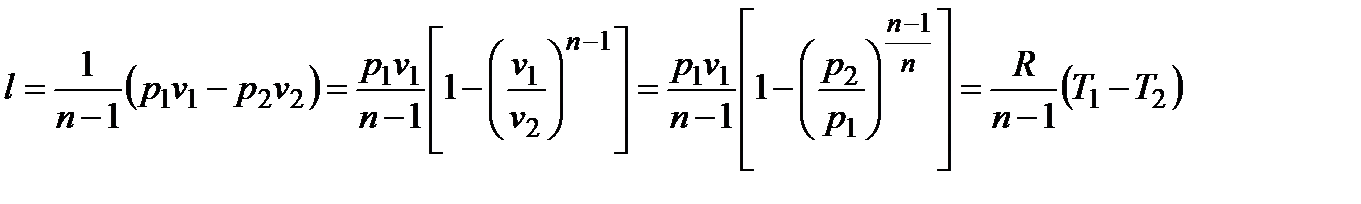 ;
; 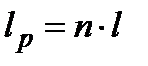 ;
; 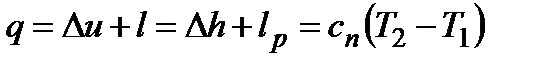
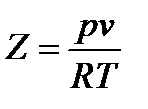 для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры.
для идеальных газов равен единице, а для реальных газов имеет сложную зависимость от давления и температуры.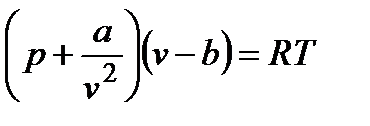 , где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует
, где a, b – константы, которые наряду с газовой постоянной характеризуют индивидуальные свойства вещества. Если сравнить это уравнение с уравнением Клапейрона pv = RT, то видно, что вместо р в нем фигурирует 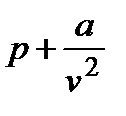 , а вместо v стоит
, а вместо v стоит 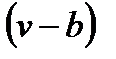 . Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член
. Согласно уравнению Клапейрона при стремлении давления к бесконечности удельный объем стремится к нулю, а из уравнения Ван-дер-Ваальса следует, что в этом случае v ® b. Следовательно, величину b можно интерпретировать как объем занимаемый собственно молекулами. Член 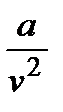 учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества
учитывает взаимодействие молекул газа. Эту величину можно рассматривать как внутреннее давление в газе. Константы a и b могут быть вычислены через критические параметры вещества 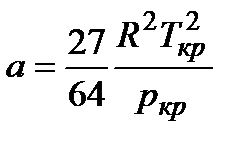 ,
, 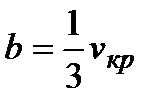 . В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно.
. В этих выражениях Ткр – критическая температура, ркр – критическое давление, vкр – критический удельный объем. Уравнение Ван-дер-Ваальса только качественно отражает поведение веществ и для точных расчетов не пригодно.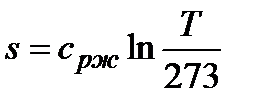
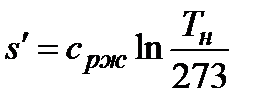
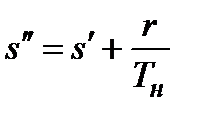
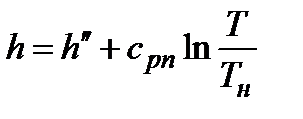
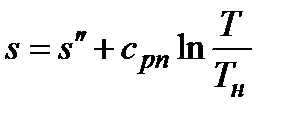
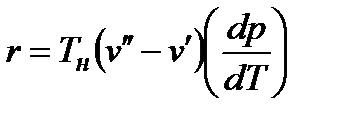 , где
, где 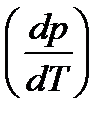 – наклон линии фазового перехода в координатах р, Т.
– наклон линии фазового перехода в координатах р, Т.