Dalton's Law of Partial Pressures

As we know, air is not a single compound but mixture of gases like nitrogen, oxygen etc. The pressure contribution of each gas is called its partial pressure. Partial pressure can thus be defined as pressure exerted if that gas alone had occupied the volume of gases¢s mixture at the same temperature. Thus the total pressure of air would be sum of partial pressures of nitrogen, oxygen etc.

This law states that the total pressure of a mixture of nonreacting gases is the sum of their individual partial pressures.

P_total = P_a + P_b + P_c + ... or

P_total = n_aRT / V + n_bRT / V + n_cRT / V + ... or

P_total = (n_a+ n_b+ n_c+ ... ) RT / V

The pressure in a flask containing a mixture of 1 mole of 0.20 mole O₂ and 0.80 mole N₂ would be the same as the same flask holding 1 mole of O₂.

Partial pressures are useful when gases are collected by bubbling through water (displacement). The gas collected is saturated in water vapor which contibutes to the total number of moles of gas in the container.

Dalton derived the law of partial pressures from his work on the amount of water vapor that could be absorbed by air at different temperatures. It is therefore fitting that this law is used most often to correct for the amount of water vapor picked up when a gas is collected by displacing water. Suppose, for example, that we want to collect a sample of O₂ prepared by heating potassium chlorate until it decomposes.

2 KClO3(s)

2 KCl(s)

+

3 O2(g)

The gas given off in this reaction can be collected by filling a flask with water, inverting the flask in a trough, and then letting the gas bubble into the flask as shown in the figure below.

Because some of the water in the flask will evaporate during the experiment, the gas that collects in this flask is going to be a mixture of O₂ and water vapor. The total pressure of this gas is the sum of the partial pressures of these two components.

P_T = P_oxygen + P_water

The total pressure of this mixture must be equal to atmospheric pressure. (If it was any greater, the gas would push water out of the container. If it was any less, water would be forced into the container.) If we had some way to estimate the partial pressure of the water in this system, we could therefore calculate the partial pressure of the oxygen gas.

By convention, the partial pressure of the gas that collects in a closed container above a liquid is known as the vapor pressure of the liquid. If we know the temperature at which a gas is collected by displacing water, and we assume that the gas is saturated with water vapor at this temperature, we can calculate the partial pressure of the gas by subtracting the vapor pressure of water from the total pressure of the mixture of gases collected in the experiment.

Non-Ideal Gases

The ideal gas equation (PV=nRT) provides a valuable model of the relations between volume, pressure, temperature and number of particles in a gas. As an ideal model it serves as a reference for the behavior of real gases. The ideal gas equation makes some simplifying assumptions which are obviously not quite true. Real molecules do have volume and do attract each other. All gases depart from ideal behavior under conditions of low temperature (when liquefaction begins) and high pressure (molecules are more crowed so the volume of the molecule becomes important). Refinements to the ideal gas equation can be made to correct for these deviations.

In 1873 J. D. van der Waals proposed his equation, known as the van der Waals equation. As there are attractive forces between molecules, the pressure is lower than the ideal value. To account for this the pressure term is augmented by an attractive force term a/V². Likewise real molecules have a volume. The volume of the molecules is represented by the term b. The term b is a function of a spherical diameter d known as the van der Waals diameter. The van der Waals equation fornmoles of gas is:

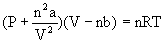
References

1. Petrucci, Ralph H. General Chemistry: Principles and Modern Applications. 9th Ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2007.

2. Staley, Dennis. Prentice Hall Chemistry. Boston, MA: Pearson Prentice Hall, 2007.

3. Olander, Donald R. "Chapter2 Equation of State." General Thermodynamics. Boca Raton, NW: CRC, 2008. Print

4. O'Connell, John P., and J. M. Haile. "Properties Relative to Ideal Gases." Thermodynamics: Fundamentals for Applications. Cambridge: Cambridge UP, 2005. Print.

5. Ghare, Shakuntala. "Ideal Gas Laws for One Component." Ideal Gas Law, Enthalpy, Heat Capacity, Heats of Solution and Mixing. Vol. 4. New York, NY, 1984. Print. F.

6. http://www.sparknotes.com/testprep/books/sat2/chemistry/chapter5section6.rhtml