Многопериодная модель потребления
Предположения:
Þ налоги и трансферты отсутствуют,
Þ потребитель имеет (до начала первого периода) первоначальные активы B0 (наследство),
Þ потребитель может свободно занимать и давать взаймы по одинаковой ставке процента,
Þ цены фиксированы и нет необходимости проводить различие между номинальной и реальной процентной ставкой.
Пусть доход потребителя (доход, не связанный с активами) в периоде t равен Yt. Тогда активы периода t будут равны: 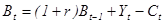 .
.
Сбережения периода t равны 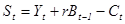 .
.
Многопериодное бюджетное ограничение.
Упрощающие предпосылки: два периода, В0=0 и В2=0, тогда:
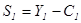 и
и 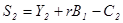 .
.
Поскольку 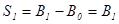 и
и 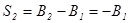 , то
, то 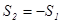 , откуда получаем двухпериодное бюджетное ограничение: C1(1+r)+C2=Y1(1+r)+Y2.
, откуда получаем двухпериодное бюджетное ограничение: C1(1+r)+C2=Y1(1+r)+Y2.
Вопрос: как изменится бюджетное ограничение, если потребитель имеет (до начала первого периода) первоначальные активы B0 и собирается в конце второго периода оставить наследство своим потомкам, равное величине B2?
Задача максимизации полезности при бюджетном ограничении:
max u(C1, C2)
C1(1+r)+C2=Y1(1+ r)+Y2
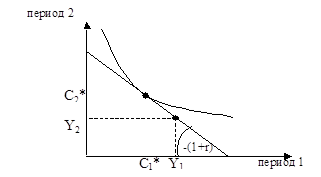
Рис 1. Графическое представление двухпериодной модели потребления
Выводы: текущее потребление 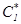 зависит:
зависит:
Þ не только от текущего дохода Y1 , но и от будущего дохода Y2;
Þ от ставки процента.
Таблица 1. Влияние роста ставки процента на текущее потребление
| Эффект Замещения | Эффект Дохода | Совокупный эффект | |
| Чистый заемщик (С1*>Y1) | - | - | - |
| Чистый кредитор (С1*<Y1) | - | + | -/+ |
Вопрос: при каком условии совокупное потребление отрицательно зависит от ставки процента?
Дата добавления: 2018-11-25; просмотров: 331;
