ОСОБЕННОСТИ РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ИЗГИБАЕМЫХ БАЛОЧНЫХ ЖБК С УЧЕТОМ ПЕРЕРАСПРЕДЕЛЕНИЯ МОМЕНТОВ ПО МЕТОДУ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
В предельном равновесии – непосредственно перед разрушением – изгибающие моменты в статически неопределимой балки находят статическим или кинематическим способом.
Статический способ. Пролетный момент (рис. 32.1) графически определим следующим образом
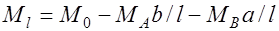 . (32.1)
. (32.1)
Отсюда уравнение равновесия можно представить в виде:
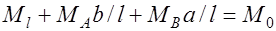 , (32.2) где
, (32.2) где 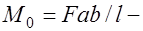 момент статически определимой свободно лежащей балки.
момент статически определимой свободно лежащей балки.
Из уравнения (32.2) следует, что сумма пролетного момента в сечении и долей опорных моментов, соответствующих этому сечению, равна моменту простой балки 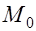 (балочному моменту). Кроме того, из уравнения (32.2) вытекает, что несущая способность статически неопределимой конструкции не зависит от соотношения значений опорных и пролетного моментов и не зависит от последовательности образования пластических шарниров. Последовательность эта может быть назначена произвольно, необходимо лишь соблюдать уравнение равновесия (32.2). Однако изменение соотношения моментов в сечениях меняют значение нагрузки, вызывающей образование первого и последнего пластических шарниров, а также меняет ширину раскрытия трещин в первом пластическом шарнире.
(балочному моменту). Кроме того, из уравнения (32.2) вытекает, что несущая способность статически неопределимой конструкции не зависит от соотношения значений опорных и пролетного моментов и не зависит от последовательности образования пластических шарниров. Последовательность эта может быть назначена произвольно, необходимо лишь соблюдать уравнение равновесия (32.2). Однако изменение соотношения моментов в сечениях меняют значение нагрузки, вызывающей образование первого и последнего пластических шарниров, а также меняет ширину раскрытия трещин в первом пластическом шарнире.
Кинематический способ. Этот способ основан на методе виртуальных перемещений. Балку в предельном равновесии рассматривают как систему жестких звеньев, соединенных друг с другом в местах излома пластическими шарнирами (рис. 32.1). Если перемещение балки под действием силы 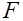 равно
равно 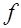 , то углы поворота звеньев
, то углы поворота звеньев
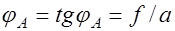 ;
; 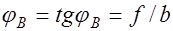 . (32.3)
. (32.3)
Виртуальная работа силы 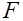 определится следующим образом:
определится следующим образом:
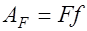 . (32.4)
. (32.4)
Виртуальная работа предельных моментов определится следующим образом:
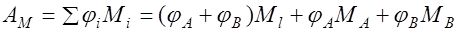 . (32.5)
. (32.5)
Учитывая зависимости (32.3) выражение (32.5) можно представить в виде:
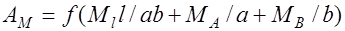 . (32.6)
. (32.6)
Согласно методу возможных перемещений для обеспечения предельного равновесия балки должно выполняться уравнение виртуальных работ:
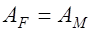 или
или 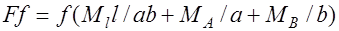 , (32.7) откуда расчетная предельная нагрузка определится следующим образом:
, (32.7) откуда расчетная предельная нагрузка определится следующим образом:
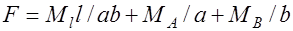 . (32.8)
. (32.8)
Если домножить левую и правую части уравнения (32.8) на 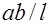 , то получим найденное выше статическим способом уравнение равновесия (32.2).
, то получим найденное выше статическим способом уравнение равновесия (32.2).
Расчет и конструирование статически неопределимых железобетонных балочных конструкций по методу предельного равновесия дает возможность облегчить армирование сечений, что особенно важно для монтажных стыков на опорах сборных конструкций, а также позволяет стандартизировать и осуществить в необходимых случаях одинаковое армирование тех зон, где при расчете по упругой схеме возникают различные по значению изгибающие моменты.
Значение перераспределенных усилий не оговаривают, но при этом необходимо выполнить расчет по предельным состояниям второй группы.
32.2. СТАТИЧЕСКИЙ РАСЧЕТ МНОГОПРОЛЕТНОГО НЕРАЗРЕЗНОГО РИГЕЛЯ ПЕРЕКРЫТИЯ
В общем случае ригели перекрытий многоэтажных зданий являются элементами рамной конструкции. В промышленном строительстве используются ригели прямоугольного, таврового сечения с полкой внизу, вверху или по середине высоты номинальным пролетом 3, 6, 9 и 12 м (рис. 32.2). В гражданских зданиях преимущественно применяют ригели с полкой внизу (рис. 32.3). При этом уменьшается строительная высота перекрытия и улучшается интерьер помещения. Пролеты ригелей унифицированы и принимаются в пределах от 3 м до 9 м. При длине ригелей 6 м и более предусматривается предварительное напряжение арматуры. Высота ригеля зависит от пролета и нагрузки и назначается в пределах 1/8…1/12 от пролета. Усилия в ригелях определяются из статического расчета рамы. С небольшой погрешностью при свободном опирании концов ригеля на несущие стены ригели можно рассчитывать как неразрезные многопролетные балки по методу предельного равновесия.
При опирании на ригель пустотных плит или плит сплошного сечения полная нагрузка на него равномерно распределена, а при опирании ребристых плит – сосредоточена в местах опирания ребер. Однако, если количество сосредоточенных сил в пролете более четырех, то их можно заменить распределенной нагрузкой. Расчетный пролет ригелей принимается равным расстоянию между осями колонн. При опирании ригеля одним концом на наружную стену расчетный пролет принимается равным расстоянию от оси колонны до центра опоры на стене.
Расчет ригеля по методу предельного равновесия с учетом перераспределения усилий позволяет упростить армирование и дает экономию арматуры по сравнению с упругим расчетом до 20%. Перераспределение усилий возникает за счет образования в ряде наиболее напряженных сечений пластических шарниров. В этом случае несущая способность конструкций определяется предельными моментами, действующими в пластических шарнирах, а эти моменты – армированием соответствующих сечений. Уменьшая или увеличивая армирование от дельных сечений, можно менять несущую способность конструкции в целом. Это дает возможность распределить усилия в конструкции без изменения несущей способности ее в целом. При расчете неразрезных железобетонных ригелей обычно применяется статический способ метода предельного равновесия. Изменение распределения усилий в этом способе достигается добавлением к эпюрам «упругих» моментов дополнительных, «перераспределяющих». Какое бы ни было распределение усилий в упругой стадии работы конструкции, последующие деформации в пластических шарнирах перераспределяют эти усилия в соответствии с армированием основных расчетных сечений. Поэтому проектировщик вправе перераспределить усилия таким образом, чтобы в итоге получить наиболее целесообразные суммарные эпюры усилий в конструкции. Однако, если предусмотреть слишком сильное перераспределение усилий, то уже при эксплуатационных нагрузках в конструкции могут появиться значительные трещины в тех сечениях, где в последствии должны образоваться пластические шарниры. Расчеты неразрезного ригеля производят в следующем порядке. В начале ведут расчет ригеля как упругой балки обычными приемами строительной механики. Рекомендуется, например, использовать пакет прикладных программ СМК, утвержденный Госстроем РФ. Расчет упругой неразрезной балки в отдельных случаях можно вести по таблицам справочника проектировщика. Тогда моменты и поперечные силы в сечениях балки для равномерно распределенной нагрузки определятся по формулам:
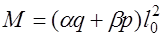 ;
; 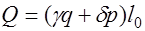 , (32.9) а для сосредоточенных нагрузок – по формулам:
, (32.9) а для сосредоточенных нагрузок – по формулам:
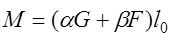 ;
; 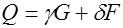 , (32.10) где
, (32.10) где 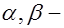 табличные коэффициенты, используемые при определении моментов от соответствующих схем загружения постоянной и временной нагрузками;
табличные коэффициенты, используемые при определении моментов от соответствующих схем загружения постоянной и временной нагрузками; 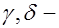 то же, но при определении поперечных сил;
то же, но при определении поперечных сил; 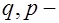 равномерно распределенные длительные и кратковременные нагрузки;
равномерно распределенные длительные и кратковременные нагрузки; 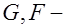 то же, но сосредоточенные.
то же, но сосредоточенные.
Постоянные нагрузки действуют всегда и во всех пролетах ригеля, а временную – рассматривают при не выгоднейших расположениях. При расположении временной нагрузки через пролет получают максимальные моменты в загружаемых пролетах, а при расположении временной нагрузки в двух смежных пролетах и далее через один пролет получают максимальные по абсолютному значению моменты на опоре (рис.32.4).
После упругого расчета необходимо построить огибающие эпюры моментов и поперечных сил от различных схем загружения постоянной и временной нагрузками (рис. 32.5). В неразрезном ригеле целесообразно ослабить армирование опорных сечений и упростить монтажные стыки. Поэтому с целью перераспределения моментов в ригеле к эпюрам моментов от постоянных нагрузок и отдельных схем не выгодно расположенных временных нагрузок добавляют треугольные эпюры с произвольными по знаку и значению над опорными ординатами. При этом ординаты выравненных эпюр моментов в расчетных сечениях должны составлять не менее 70% от вычисленных по упругой схеме. Для этого находят семидесяти процентные значения наибольших по абсолютной величине опорных моментов. После этого выбором «перераспределяющих» эпюр добиваются того, чтобы каждый из опорных моментов, превышающих по абсолютной величине выбранное семидесяти процентное значение, свести к этому значению. Если какой-либо опорный момент при данном сочетании по абсолютной величине меньше выбранного семидесяти процентного значения, то этот момент целесообразно довести до этого семидесяти процентного значения. Если неразрезной ригель имеет более пяти пролетов, то его практически заменяют пяти пролетным, так как моменты в средних пролетах такие же, что и в третьем пролете пяти-пролетного ригеля. Погонная нагрузка на ригель собирается с грузовой полосы, равной расстоянию между ригелями.
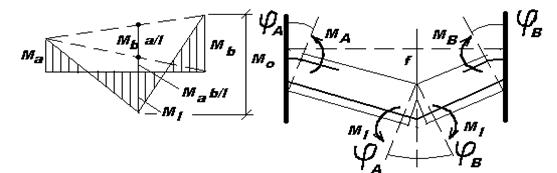 |
Рис. 32.1




































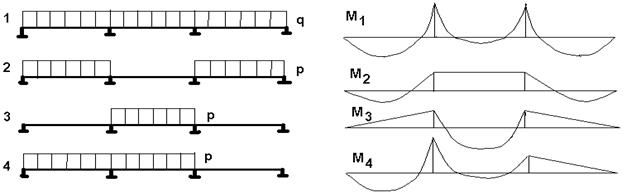 |
Рис. 32.2 Рис. 32.3
Рис. 32.4
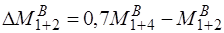 ;
; 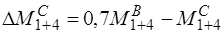
Рис. 32.5
| <== предыдущая лекция | | | следующая лекция ==> |
| ОСОБЕННОСТИ КОНСТРУИРОВАНИЯ СБОРНЫХ ПЛИТ ПЕРЕКРЫТИЯ | | | ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ ТЕЛА СБОРНОГО РИГЕЛЯ ПЕРЕКРЫТИЯ |
Дата добавления: 2018-09-24; просмотров: 1602;
