Закон Больцмана о равномерном распределении энергии по степеням свободы молекул.

Как известно, наименьшими количествами элемента или вещества, сохраняющими их химические свойства, являются атомы и молекулы. На практике мы, однако, имеем дело не с отдельными атомами и молекулами, а с макроскопическими телами, состоящими из огромного числа атомов или молекул. Даже такое малое количество вещества, как моль, содержит огромное число молекул, равное числу Авогадро (N_A = 6.02*10²³ моль^-1). Возьмем для примера 1 мл воды, масса этой воды 1 г, что составляет 1/18 моля воды. Значит, в 1 мл воды содержится N_A/18 = 3.34*10²² молекул.

Наблюдения убеждают, что во всяком веществе имеется непрерывное внутреннее движение – это движение молекул, из которых оно состоит. Это движение беспорядочное, оно никогда не прекращается. В том, что такое движение действительно имеет место, убеждает следующий опыт. Представим себе два сосуда, соединенных друг с другом трубкой с краном. Заполним при закрытом кране один сосуд азотом, а другой – водородом. Открыв кран, через какое-то время убеждаемся, что в обоих сосудах находится совершенно равномерная смесь газов. Такой результат был бы невозможен, если бы молекулы азота и водорода не совершали движения, за счет которого они и перемешиваются.

Еще более отчетливо о существовании хаотического движения молекул свидетельствует явление броуновского движения малых частиц вещества, взвешенных в жидкости. Броун заметил, наблюдая за частицами взвеси в микроскоп, что, чем меньше частица, тем интенсивнее и хаотичнее она движется. Траектории движения частиц можно описать ломаными пересекающимися линиями. Это беспорядочное броуновское движение обусловлено тем, что частицы взвешенного в жидкости вещества велики по сравнению с молекулами жидкости. Они испытывают со всех сторон удары молекул, которые сообщают им некоторое количество движения. Если частица достаточно велика, то за счет большой поверхности она испытывает примерно одинаковое – хоть и огромное – число ударов с противоположных сторон, поэтому частица таких размеров почти не меняет своего положения. В случае же мелких частиц из-за их меньшей поверхности число ударов с противоположных сторон могут оказаться нескомпенсированными: с одной стороны частицу ударит больше молекул, чем с другой, и частица придет в движение.

Движение молекул в широком смысле слова изучает молекулярная физика, которая имеет дело с множествами молекул. Разумеется, в случае, например, газа, мы не можем определить движение каждой из них, мы можем оперировать лишь какими-то средними характеристиками, и эти средние характеристики уже не содержат элементы случайности, а принимают при определенных условиях вполне определенные значения. Иными словами, беспорядочность, хаотичность движения каждой отдельной молекулы ведет к наличию определенных закономерностей, связывающих средние значения очень большого числа элементарных процессов. Когда мы наблюдаем явления в малых масштабах, когда число молекул невелико, встречаются отклонения от средних значений, которые называются флуктуациями.

Метод, применяемый для описания макроскопических свойств тел с точки зрения их молекулярного строения есть метод статистический. Этот метод позволяет вычислять вероятность протекания того или иного процесса в коллективе молекул при данных условиях опыта, который может быть повторен неограниченное число раз. Понятно, что вероятность определяется не точно, а приближенно, а степень приближения возрастает с ростом числа повторений опыта. Знание вероятностей позволяет определить средние значения различных физических величин, которые описывают поведение всей системы в целом.

В молекулярной физике важную роль играет понятие термодинамической системы, под которым понимается совокупность макроскопических тел, которые могут обмениваться энергией между собой и с внешней средой, т. е. с другими телами. Термодинамическая система может находиться в разных состояниях, отличающихся друг от друга параметрами состояния: массой, температурой, давлением, объемом, плотностью и т. д. Состояния, в которых хотя бы один из параметров системы не имеет определенного значения, называются неравновесными. И наоборот: если все параметры системы не изменяются со временем, система будет называться равновесной.

Раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, а также закономерности переходов систем между такими состояниями, называется термодинамикой. В отличие от статистического метода термодинамика не рассматривает микропроцессы, которые лежат в основе таких превращений. Ее не интересует ни микроскопическое строение вещества, ни механизм явлений, она устанавливает лишь связи между макроскопическими свойствами вещества, оперируя названными параметрами системы. Термодинамический подход не противоречит статистическому методу, они просто дополняют друг друга при изучении термодинамических систем.

Итак, молекулы газа хаотически движутся. А каким образом можно определить скорости их движения? Как оказалось, такую возможность дают опыты с молекулярными пучками, одним из которых является опыт Штерна. По оси цилиндрического сосуда радиуса R проходит проволока, покрытая слоем серебра и окруженная соосным цилиндром меньшего радиуса со щелевым отверстием а, параллельным оси цилиндров (рис. 2.2.1). При нагревании проволоки электрическим током серебро испаряется, давая молекулярный пучок, который пролетает щель а и попадает в точку А внешнего цилиндра. Если же всю конструкцию привести во вращение вокруг ее оси, пучок будет попадать в точку В. Если R – радиус внешнего цилиндра, то пучок достигнет точку В через среднее время

А

• В

R

Рис. 2.2.1.

t_ср = R/V_ср, (2.2.1)

где V_ср – средняя скорость движения молекул. За это время каждая точка на стенке внешнего цилиндра, куда попал молекулярный пучок, пройдет путь (расстояние от т. А до т. В)

S = ωRt_ср, (2.2.2)

где ω – угловая скорость вращения цилиндра. Откуда

t_ср = S/ωR. (2.2.3)

Приравнивая 2.2.1 и 2.2.3 друг к другу, получим

V_ср = ωR²/S. (2.2.4)

Поскольку молекулы газа (паров серебра) движутся с различными скоростями, то след В оказывается размазанным, но положение середины следа определить несложно, откуда можно найти среднюю скорость движения молекул серебра V_ср. При этом каждой температуре проволоки отвечает некоторая наиболее вероятная скорость V_в такая, что большинство молекул движутся со скоростями, не очень сильно отличающимися от V_в.

Ввиду беспорядочности движения молекул некорректно ставить вопрос о числе молекул, которые обладают точно заданной скоростью. Однако можно говорить о числе молекул, скорости которых лежат в некотором интервале. Максвелл, пользуясь теорией вероятности, подсчитал относительное число молекул dn(V)/n из общего числа молекул в ансамбле n, скорости которых лежат в интервале от V до V + dV. Функция F(V) = dn(V)/ndV, определяющая это относительное число, имеет вид

F(V) = 4π(m/2πkT)^3/2V²exp(–mV²/2kT) (2.2.5)

и носит название функции Максвелла распределения молекул идеального газа по скоростям. Отметим, что под знаком экспоненты стоит выражение mV²/2kT, равное отношению кинетической энергии mV²/2 к среднему значению kT этой энергии.

Найдем наиболее вероятную скорость V_в. Для этого продифференцируем V²exp(–mV²/2kT) по dV и приравняем производную к нулю. В нашем случае с учетом того, что мы имеем произведение двух сомножителей, зависящих от V, получим

exp(–mV²/2kT)(2 – mV²/kT)V = 0. (2.2.6)

Проанализируем это выражение. В 2.2.6 первый сомножитель из трех – экспонента – обращается в ноль при V = ∞, а третий – V – при V = 0. Однако оба эти случая отвечают минимумам функции F(V), ее максимум будет наблюдаться при

(2 – mV²/kT) = 0, (2.2.7)

откуда

V_в = (2kT/m)^1/2. (2.2.8)

Средняя арифметическая скорость

V_ср = (8kT/πm)^1/2, (2.2.9)

а среднеквадратичная скорость

V_ср/кв = (3kT/m)^1/2. (2.2.10)

V_в, V_ср и V_ср/кв соотносятся друг с другом как отношение чисел 1.00, 1.13 и 1.22. График функции Максвелла приведен на рис. 2.2.2.

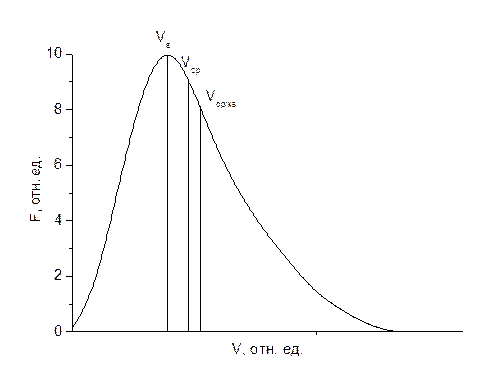
Рис. 2.2.2.

При выводе основного уравнения молекулярно-кинетической теории газа и максвелловского распределения молекул по скоростям считалось, что на молекулы газа внешние силы не действуют, вследствие чего можно было считать, что молекулы равномерно распределены по объему. Однако молекулы находятся в поле тяготения Земли, что приводит к убыванию давления газа с высотой. Будем считать, что поле тяготения однородно, температура не изменяется по высоте, а масса всех молекул одинакова. Если на высоте h давление равно p, то на высоте h + dh оно равно p + dp. Разность давлений dp должна быть равна весу газа в объеме цилиндра высотой dh и площадью, равной единице:

dp = – ρgdh, (2.2.11)

где ρ – плотность газа на высоте h. Из уравнения Клапейрона – Менделеева находим

ρ = m/v = pM/RT. (2.2.12)

Подставим это выражение в 2.2.11, получим

dp = – Mgpdh/RT, (2.2.13)

или

dp/p = – Mgdh/RT. (2.2.14)

При изменении высоты от h₁ до h₂ давление изменяется от р₁ до р₂, поэтому можно записать, что интеграл от dp/p в пределах от р₁ до р₂ равен со знаком минус интегралу от dh в пределах от h₁ до h₂, умноженному на Mg/RT. После взятия интегралов получим

ln(p₂/p₁) = – (h₂ – h₁)Mg/RT, (2.2.15)

или

p₂ = p₁exp( – (h₂ – h₁)Mg/RT). (2.2.16)

Выражение 2.2.16 называется барометрической формулой. Обычно ее записывают в несколько иной форме

p = p₀exp( – Mgh/RT), (2.2.17)

где p₀ – давление на уровне моря, а р – давление на высоте h.

Как уже не раз отмечалось, молекулы, двигаясь хаотически, непрерывно сталкиваются друг с другом. Между двумя столкновениями они проходят некоторый путь l, который называется длиной свободного пробега. Понятно, что эти пути для каждой пары столкновений свои, но, поскольку речь идет об огромном числе молекул, которые находятся в движении, можно говорить о средней длине свободного пробега молекул<l>. Чтобы найти ее, представим, что молекулы имеют диаметр d. За 1 с молекула преодолевает путь, численно равный средней арифметической скорости ее движения, поэтому, если за это время молекула испытывает среднее число столкновений <z>, то средняя длина свободного пробега молекул

<l> = <V>/<z>. (2.2.18)

Понятно, что на своем пути молекула столкнется с теми молекулами, центры которых находятся по отношению к направлению движения на расстояниях, равных или меньших d. Среднее число столкновений молекулы за 1 с будет равно числу молекул в объеме цилиндра с основанием πd² и высотой <V>, т. е.

<z> = n πd²<V>, (2.2.19)

где n – концентрация молекул. С учетом движения других молекул 2.2.19 превращается в

<z> = √2 n πd²<V>. (2.2.20)

Тогда средняя длина свободного пробега

<l> = 1/√2 n πd². (2.2.21)

Таким образом, средняя длина свободного пробега обратно пропорциональна концентрации молекул, которая, в свою очередь, пропорциональна давлению. Значит, можно записать следующее соотношение:

<l₁>/<l₂> = n₂/n₁ = p₂/p₁. (2.2.22)

В физике существует понятие числа степеней свободы, под которым понимают число независимых переменных, которые полностью определяют положение тела в пространстве. Материальной точке приписывают три степени свободы поступательного движения. Двухатомные молекулы имеют пять степеней свободы: три степени для поступательного движения и две – для вращательного движения (вращение вокруг оси, проходящей через центры атомов, лишено смысла. Трехатомная и многоатомная молекулы имеют шесть степеней свободы: три для поступательного движения и три – для вращательного. Для реальных молекул учитывают также степени свободы колебательного движения.

В случае поступательного движения ни одна из степеней свободы не имеет преимущества перед двумя другими, поэтому на каждую из них приходится одинаковая энергия, равная 1/3 от энергии <ε₀>, поэтому

<ε₁> = <ε₀>/3 = kT/2. (2.2.23)

Больцман сформулировал закон о равномерном распределении энергии по степеням свободы молекул:для системы, находящейся в состоянии термодинамического равновесия, на каждую степень поступательного и вращательного движения приходится кинетическая энергия, равная kT/2, а на каждую степень свободы колебательного движения, – энергия, равная kT. Таким образом, средняя энергия молекулы

<ε>= ikT/2, (2.2.24)

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы.

Контрольные вопросы

1. В чем особенности статистического и термодинамического подходов к изучению газовых систем?

2. Что такое броуновское движение частиц вещества малых размеров, чем оно вызвано и о чем свидетельствует?

3. Как проводился опыт Штерна и что он показал?

4. О чем говорит закон Максвелла о распределении молекул идеального газа по скоростям?

5. Как соотносятся друг с другом наиболее вероятная, средняя и среднеквадратичная скорости движения молекул газа?

6. Как выглядит барометрическая формула и что она означает?

7. Что такое длина свободного пробега молекул? От чего она зависит? Каким образом?

8. Что понимают под степенями свободы механического движения элементов молекулярных систем?

9. Как распределяется энергия по степеням свободы поступательного, вращательного и колебательного видов движения? Кто автор соответствующего закона?