Кривые безразличия и их анализ.

Графически система предпочтений потребителя изображается с помощью кривых безразличия (впервые применены английским экономистом Ф.Эджуортом в 1881 г.),

Кривая безразличия - кривая, состоящая из точек, каждая из которых представляет такую комбинацию двух видов товаров (х и у), что потребителю безразлично, какую ему выбрать. Другими словами, кривая безразличия показывает альтернативные наборы товаров, обеспечивающие одинаковый уровень полезности (рис. 4.2).

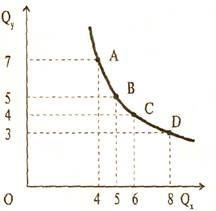
Рис. 4.2. Кривая безразличия.

На представленной кривой безразличия мы выделили четыре равнополезные комбинации двух благ в точках А, В, С, D. Эти комбинации дают потребителю одинаковое общее удовлетворение, т.е. А ~ В ~ С ~ D.

Комбинации благ, представляющие для потребителя большую или меньшую полезность, будут находиться либо выше, либо ниже нашей кривой безразличия. Любая точка, взятая наобум, вместе с другими точками, дающими ту же величину удовлетворения, может образовать кривую безразличия.

Набор кривых безразличия для одного потребителя и одной пары благ образует карту безразличия (рис. 4.3).

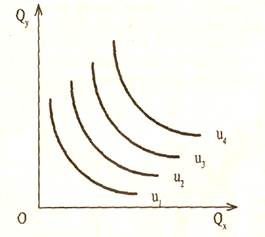
Рис. 4.3 Карта безразличия.

Свойства кривых безразличия вытекают из тех аксиом, на которых базируется порядковый подход:

1. Наборы на кривых безразличия, более удаленных от начала координат, обеспечивают потребителю большую полезность, а потому - предпочтительнее, чем наборы на менее удаленных кривых. Это вытекает из предположения, что большее количество благ предпочитается меньшему.

2. Касательная, проведенная к любой точке кривой безразличия, имеет отрицательный угол наклона.

3. Кривые безразличия не пересекаются.

Предельной нормой замены благом х блага у (MRS_хy) называется количество блага у, которое должно быть сокращено при увеличении блага х на одну единицу так, чтобы уровень удовлетворения потребителя не изменился.

MRS_XY = - ΔУ

ΔХ

Если потребитель при выборе другого набора желает остаться на той же кривой безразличия, то прирост полезности от добавленного Q должен быть равен потере полезности от изъятого Q , то есть:

ΔQx • MUx = -ΔQy • MUy → ΔQy/ΔQx = MUx/MUy = MRSху

Значит, предельная норма замены благом х блага у может рассматриваться как отношение предельной полезности блага х к предельной полезности блага у. Поскольку MUx уменьшается по мере замены товаром х товара у, a MUу соответственно, увеличивается, отношение-MUx/MUy , равное MRS , уменьшается. Это проявляется на графике в убывании углового коэффициента наклона касательной по мере движения вниз вдоль кривой безразличия и объясняет ее вогнутый характер. Последнее означает, что в окрестности любой своей точки она находится выше касательной, проведенной к этой точке.

Из вышеизложенного вытекает еще одно замечание. Уменьшающаяся предельная норма замены в порядковой теории имеет тот же смысл, что и убывающая предельная полезность в количественной теории. Только во втором случае полезность каждой дополнительной единицы товара оценивается в ютилах, а в первом - объемом другого товара, от которого потребитель готов отказаться.

Вогнутый характер кривых безразличия - наиболее общая и распространенная ситуация. Однако условие уменьшающейся предельной нормы замены не всегда соблюдается. Для товаров, жестко взаимодополняющих друг друга (лыжи и крепления к ним), кривые безразличия имеют L-образный вид (рис. 4.4). Здесь MRS = 0, так как эти блага не могут заменяться. Нулевая предельная норма замены характерна и для тех ситуаций, когда потребитель не поступится даже бесконечно малым количеством товара в пользу другого.

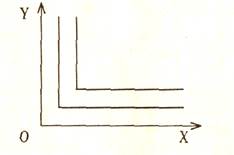
Рис. 4.4. Жесткая взаимодополняемость благ, MRS = 0.

Для двух совершенно взаимозаменяемых товаров кривые безразличия представляют собой прямые линии, имеющие отрицательный наклон. Это случай, когда оба товара воспринимаются потребителем как один, и MRS - постоянная величина (рис.3.5)

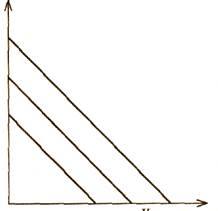
Рис.4.5 Совершенная взаимозаменяемость, MRS = const.