Особые виды ритмического деления длительностей
Современная нотация исходит из того, что каждая метрическая доля может делиться на 2, 4, 8, 16 и т.д. частей (то есть на 2 и на степени числа 2). Однако в музыкальной практике дело обстоит не всегда так. Например, четверть иногда делится не на две восьмых, а на три равные части, которые, естественно, не являются уже восьмыми. Тем не менее эти части четверти записываются как условные восьмые, однако при этом указывается цифрой, что мы имеем дело с особым делением длительностей (см. пример 44, такты 2 и 3), То же может произойти при делении такта на доли, когда такт той же длительности, что и предыдущие, делится не на две доли, а временно на три, или наоборот — трехдольный такт делится на две части.
| Деление на | 3 ч. | вместо 2 | образует | триоли |
| — »— | 2 ч. | — »— 3 | — »— | дуоли |
| — »— | 4 ч. | — »— 3 | — »— | квартоли |
| — »— | 5 ч. | — »— 4 (или 3) | — »— | квинтоли и т.д. |
Фигуры особого деления обозначаются соответствующей цифрой, которая ставится, как правило, у ребра длительностей или у квадратной скобки, используемой в тех случаях, когда ребра нет. Длительности же звуков записываются так же, как при нормальном делении, которое заменено особым. Например, если триоль заменяет две восьмые, то и записывается она восьмыми. Если же триоль заменяет две четверти, то и записывается она четвертями:
45 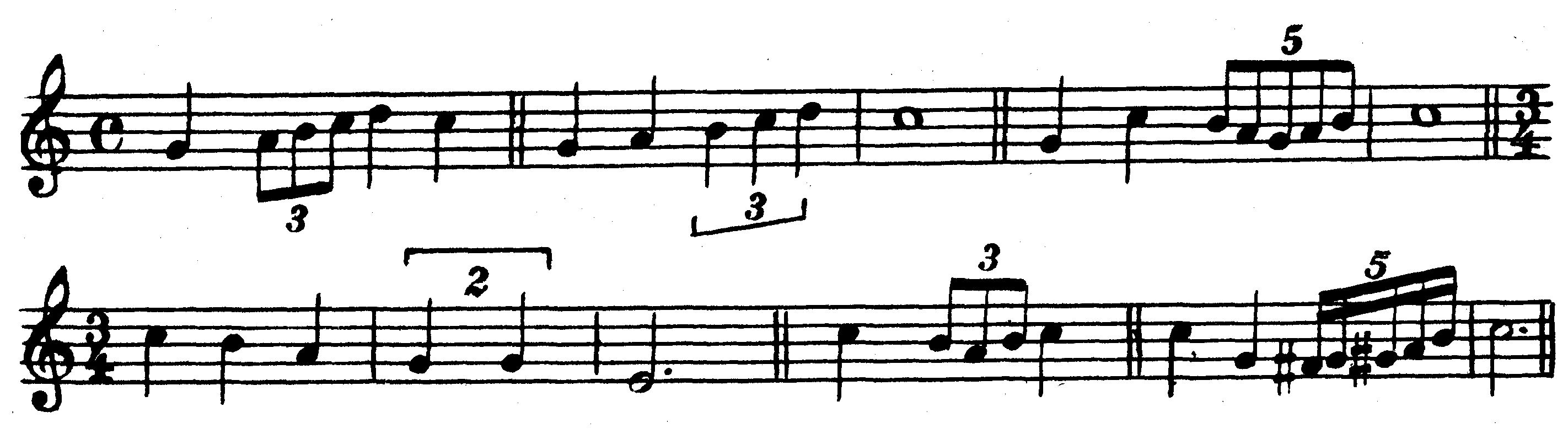
Кроме дуолей, триолей, квартолей, квинтолей могут встретиться и иные деления длительностей. Так, например, в виртуозных пассажах можно встретить деление на очень мелкие длительности, образующие группы нот, не укладывающиеся в обычное деление. Например, в следующем примере на одну восьмую приходится четырнадцать условных шестьдесятчетвертых вместо восьми:
46 [Andante non troppo e molto maestoso] Чайковский. Концерт № 1 для ф-п. с оркестром


Дата добавления: 2018-09-24; просмотров: 634;
