Классификация радиоволн
Введение в теорию ЭМП
Предмет и содержание курса. Краткая история развития учения об электромагнетизме. Роль русских учёных в развитии теории ЭМП.
ЭМП как одна из форм материи. Макроскопические и квантовые свойства ЭМП. Предмет классической электродинамики. Роль теории ЭМП в развитии науки, систем связи и вещания, телекоммуникации и др. Определение диапазонов, относящихся к области СВЧ.
Основные понятия теории ЭМП. Векторы ЭМП. Макроскопические параметры материальных сред. Материальные уравнения. Законы Ома и Джоуля в интегральной и дифференциальной формах.
Описание свойств векторных полей. Интегральные и дифференциальные характеристики физических полей. Основные теоремы векторного анализа. Операторы набла (Гамильтона) и Лапласа. Классификация векторных полей.
Указания к теме
Необходимо запомнить деление радиоволн и области СВЧ на диапазоны, выучить определения ЭМП, ЭМВ, электрического заряда, составляющих ЭМП. Необходимо вспомнить основы векторной алгебры и электромагнетизма.
Следует изучить основные этапы развития теории ЭМП, обратить внимание на принципиальные отличия диапазонов СВЧ от ВЧ и НЧ, на ограничения теории цепей и макроскопической электродинамики.
Основные сведения
В диапазонах УВЧ и СВЧ размеры устройств соизмеримы с длиной волны, поэтому приходится учитывать волновой характер ЭМП. Законы теории цепей, справедливые на более низких частотах, перестают действовать, поскольку в этом случае нельзя использовать понятие «электрическая цепь», которое позволяет существующее в системе ЭМП разделить на независимые электрические и магнитные составляющие, локализованные в соответствующих элементах электрической цепи. Поэтому при изучении быстропеременных электрических процессов необходим анализ именно ЭМП с учетом его волнового характера и конечной скорости распространения ЭМВ.
Краткая история развития теории ЭМП.Понятие поля (электрического и магнитного) впервые было введено М. Фарадеем в 30-х годах XIX века. Система уравнений Максвелла (1864) обобщила и дополнила известные в то время законы электромагнетизма. В 1888 г. радиоволны были экспериментально получены Г. Герцем.
Началом практического применения ЭМВ считаются опыты А.С. Попова, в которых в 1895 г. была продемонстрирована возможность беспроводной связи.
Теория относительности придала фундаментальный смысл понятию поля как первичной физической реальности, что позволило приравнять понятия «вещество» и «поле» как две формы существования материи. Один из важнейших выводов теории А. Эйнштейна – взаимосвязь массы и энергии (W = mc2). Квантовый эффект аннигиляции электронно-позитронной пары с выделением фотона (и обратный переход) отражает существующую в микромире связь различных видов материи (вещества и поля). В масштабах микромира проявляется корпускулярно-волновой дуализм ЭМП. Протяженное ЭМП в этом случае следует рассматривать как систему независимых дискретных микрообъектов – фотонов. В этом случае действуют законы квантовой электродинамики.
В таблице приведена классификация радиоволн по диапазонам.
Таблица
Классификация радиоволн
| Границы диапазона по частотам и длинам волн | Название диапазона по частотам и длинам волн | Сокращенное обозначение | |
| русское | международное | ||
| 3–30 кГц 100–10 км | Очень низкие частоты Мириаметровые волны (сверхдлинные волны) | ОНЧ (СДВ) | VLF |
| 30–300 кГц 10–1 км | Низкие частоты Километровые волны (длинные волны) | НЧ (ДВ) | LF |
| 300–3000 кГц 1000–100 м | Средние частоты Гектометровые волны (средние волны) | СЧ (СВ) | MF |
| 3–30 МГц 100–10 м | Высокие частоты Декаметровые волны (короткие волны) | ВЧ (КВ) | HF |
| 30–300 МГц 10–1 м | Очень высокие частоты Метровые волны (ультракороткие волны) | ОВЧ (УКВ) | VHF |
| 300–3000 МГц 100–10 см | Ультравысокие частоты Дециметровые волны (ультракороткие волны) | УВЧ (УКВ) | UHF |
| 3–30 ГГц 10–1 см | Сверхвысокие частоты Сантиметровые волны (ультракороткие волны) | СВЧ (УКВ) | SHF |
| 30–300 ГГц 10–1 мм | Крайне высокие частоты Миллиметровые волны | КВЧ | EHF |
Основные понятия теории ЭМП.Классическая (макроскопическая) электродинамика – теория поведения ЭМП, осуществляющего взаимодействие между электрическими зарядами. В этом случае ЭМП приписывают только волновые свойства и считают его непрерывным, что очень удобно в макромире.
Например, в случае излучения одиночного радиоимпульса при значительном расстоянии между передающей и приемной антеннами в какой-то момент времени окажется, что сигнал уже излучен передающей антенной, но еще не принят приемной. Следовательно, в данный момент времени энергия сигнала будет локализована в пространстве. В этом случае очевидно, что носитель энергии не является привычной вещественной средой, а представляет собой иную физическую реальность, которая называется полем.
ЭМП – это особая форма материи, посредством которой осуществляется взаимодействие между электрическими зарядами, отличающаяся непрерывным распределением в пространстве (ЭМВ, ЭМП заряженных частиц) и обнаруживающая дискретность структуры (фотоны), характеризующаяся способностью распространяться в вакууме со скоростью, близкой к с, оказывающая на заряженные частицы силовое воздействие, зависящее от их скорости [11, 12].
Электрический заряд – свойство частиц вещества или тел, характеризующее их взаимосвязь с собственным ЭМП и взаимодействие с внешним ЭМП; имеет два вида, известные как положительный заряд (заряд протона) и отрицательный заряд (заряд электрона); количественно определяется по силовому взаимодействию тел, обладающих электрическими зарядами [11, 12].
ЭМВ – ЭМ колебания, распространяющиеся в пространстве с течением времени с конечной скоростью [1].
При исследовании ЭМП обнаруживаются две формы его проявления – электрическое и магнитное поля, которым можно дать следующие определения.
Электрическое поле – одно из проявлений ЭМП, обусловленное электрическими зарядами и изменением магнитного поля, оказывающее силовое воздействие на заряженные частицы и тела, выявляемое по силовому воздействию как на неподвижные, так и на движущиеся заряженные тела и частицы.
Магнитное поле – одно из проявлений ЭМП, обусловленное электрическими зарядами движущихся заряженных частиц (и тел) и изменением электрического поля, оказывающее силовое воздействие только на движущиеся заряженные частицы, выявляемое по силовому воздействию, направленному нормально к направлению движения этих частиц и пропорциональному их скорости.
Разделение ЭМП на электрическое и магнитное поля имеет относительный характер, поскольку зависит от выбора инерциальной системы отсчета, в которой исследуется ЭМП. Например, если некоторая система состоит из покоящихся электрических зарядов, то при исследовании ЭМП в данной системе будет установлено наличие электрического поля и отсутствие магнитного. Однако если другая система координат будет двигаться относительно данной системы, то во второй системе будет обнаружено и магнитное поле [11].
Основными векторами ЭМП являются 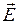 (напряженность электрической составляющей поля) и
(напряженность электрической составляющей поля) и 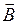 (магнитная индукция), которые описывают соответствующее проявление механических сил в ЭМП и могут быть непосредственно измерены. Напряженность электрического поля определяется как сила, действующая на точечный заряд известной величины (сила Ш. Кулона)
(магнитная индукция), которые описывают соответствующее проявление механических сил в ЭМП и могут быть непосредственно измерены. Напряженность электрического поля определяется как сила, действующая на точечный заряд известной величины (сила Ш. Кулона) 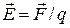 .
.
Магнитная индукция определяется через силу, действующую на точечный заряд q известной величины, движущийся в магнитном поле со скоростью 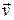 , (силу Г. Лоренца)
, (силу Г. Лоренца) 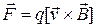 :
: 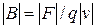 .
.
Вспомогательными векторами ЭМП являются 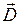 (электрическая индукция или электрическое смещение) и
(электрическая индукция или электрическое смещение) и 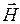 (напряженность магнитной составляющей ЭМП). Названия характеристик ЭМП сложились исторически.
(напряженность магнитной составляющей ЭМП). Названия характеристик ЭМП сложились исторически.
Единицы измерения основных характеристик ЭМП (в Международной системе единиц СИ) приведены на с. 3–4.
Связь между основными и вспомогательными векторами ЭМП осуществляется с помощью материальных уравнений
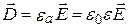 ;
; 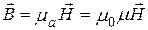 . (1.1)
. (1.1)
В большинстве сред векторы 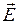 и
и 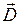 , как и
, как и 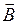 и
и 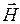 , коллинеарны. Но в случае гироэлектрических (сегнетоэлектрики) и гиромагнитных (ферромагнетики) сред e и m становятся тензорными величинами, и указанные в парах векторы могут утратить коллинеарность.
, коллинеарны. Но в случае гироэлектрических (сегнетоэлектрики) и гиромагнитных (ферромагнетики) сред e и m становятся тензорными величинами, и указанные в парах векторы могут утратить коллинеарность.
Величина s – удельная проводимость среды. С помощью этой величины можно связать плотность тока проводимостиjпр и напряженность поля следующей зависимостью:
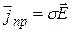 . (1.2)
. (1.2)
Уравнение (1.2) представляет собой дифференциальную форму закона Г. Ома для участка цепи.
Математический аппарат, применяемый для описания свойств векторных полей, называется векторным анализом. Важными характеристиками векторного поля являются циркуляция, поток (интегральные), градиент, дивергенция и ротор (дифференциальные) [3, гл. 2, с. 10–14]. Эти понятия пришли из физики как удобные и наглядные величины.
Дата добавления: 2018-09-24; просмотров: 1952;
