Подобие гидромеханических процессов

В инженерных задачах о движении вязкой жидкости необходимо рассчитать динамические (перепад давления 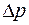или сила сопротивления тела, на которое набегает поток) или кинематические (обычно средняя скорость потока v) параметры потока.

Для определения вида зависимости потерь напора на трение (по длине) от различных влияющих на потери факторов применим метод размерностей.

Важно отметить, что составление полного и правильного перечня величин, характеризующих изучаемый процесс, - крайне ответственный этап для получения расчетных формул с помощью метода размерностей. Здесь необходимы представления о физике процесса, которые основаны на накопленном опыте гидравлических исследований.

При установившемся движении в поле сил тяжести перепад давления (или сила сопротивления тела, обтекаемого жидкостью) и средняя скорость зависят от следующих параметров:

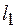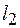1) геометрических параметров русла или трубопровода. К ним относятся форма и характерные размеры живого сечения и ; длина по направлению движения 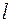; углы, ограничивающие живое сечение; форма, взаимное расположение и размеры выступов шероховатости стенок: 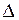- высота выступа и 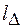- характерный продольный размер выступа шероховатости;

2) физических свойств жидкости: 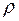- плотности, 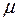- динамической вязкости, 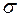- поверхностного натяжения и 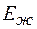- модуля упругости;

3) степени турбулизации потока, которая характеризуется в первую очередь среднеквадратичными значениями пульсационных составляющих .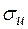

При неустановившемся движении, кроме того, к перечисленным величинам добавляется время .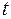

Согласно 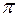-теореме уравнение, выражающее некоторую физическую закономерность и содержащее 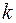размерных величин (из которых 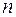величин имеют независимые размерности), может быть преобразовано в уравнение, связывающее ( 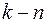) независимых безразмерных комплексов. Эти безразмерные комплексы составлены из указанных 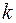величин.

Независимыми называются комплексы, которые не могут быть получены в виде степенной функции остальных комплексов.

В гидравлике в качестве параметров с независимыми размерностями принимают базовые величины: характерный линейный размер, скорость и плотность. Размерность любой другой величины в приведенном выше перечне может быть выражена через размерности базовых величин. В качестве линейного размера, характеризующего живое сечение, примем 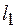характерный размер живого сечения. В различных задачах это будет или 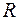- гидравлический радиус, или 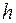глубина жидкости, или 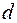диаметр трубы и т. д.

Если произвольную из указанных размерных величин, не входящую в состав параметров с независимыми размерностями, обозначить через 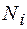, то безразмерный комплекс, характеризующий влияние данной размерной величины 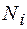на движение жидкости ( 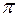-член), выражается как

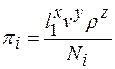. (8.1)

Могут быть применены и 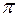-члены в виде 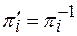. Напомним, что размерности базовых величин таковы:

.

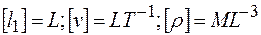В общем виде взаимосвязь между указанными величинами, включая и ускорение свободного падения 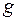, имеет вид

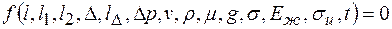, (8.2)

всего имеем 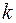=14 размерных величин. Так как величины с независимыми размерностями 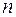=3, то в результате должны получить 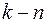=11 безразмерных комплексов (членов).

Рассмотрим применение метода размерностей для размерных величин 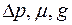и .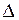

Применим (8.1) к перепаду давления .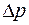

Имеем

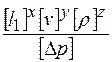
или

.

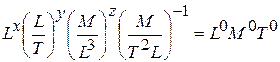Тогда

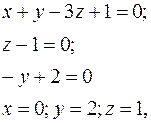
Следовательно, 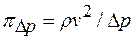или 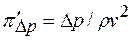. (8.3)

Безразмерный комплекс 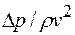называется числом Эйлера .

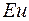Запишем (8.1) для динамической вязкости 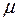, размерность которой [ ]:

,

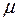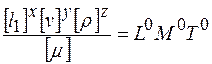отсюда

.

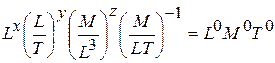Сравнивая показатели степени при одноименных размерностях в правой и левой частях, получим

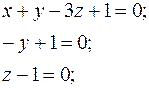
тогда .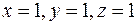

Получим

.

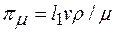Учитывая, что 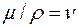кинематическая вязкость, находим, что влияние вязкости отражается безразмерным комплексом 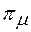, т. е. известным числом Рейнольдса

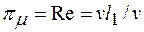. (8.4)

Для размерного члена 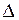получим, применяя аналогичный прием,

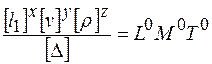
или

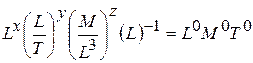
откуда

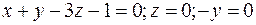и ;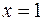

.

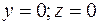Таким образом, 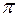-член, отражающий влияние высоты выступов шероховатости, представится в виде

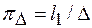или 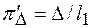. (8.5)

Следовательно, на движение жидкости оказывает влияние не абсолютное значение высоты выступа шероховатости, а безразмерная величина — относительная шероховатость 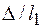. Как уже указывалось, 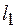- линейная величина характеризующая живое сечение русла или трубы. Это может быть диаметр 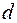или радиус трубы 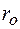, гидравлический радиус 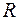, глубина безнапорного потока .

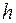Величина, обратная относительной шероховатости, т. е. 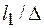, называется относительной гладкостью.

Определим 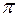-член, отражающий влияние силы тяжести, представленной в (8.2 ускорением 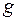. Снова применим (8.1:

;

/

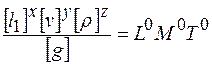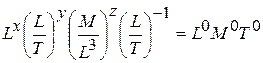Тогда

;

; .

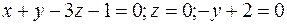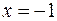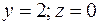Отсюда 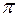-член, отражающий влияние силы тяжести на движение жидкости, равен

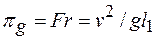. (8.6)

Этот безразмерный комплекс называется числом Фруда. В литературе применяют число Фруда в форме

.

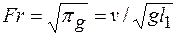Выполнив анализ размерностей и для других членов уравнения (8.2), найдем соответствующие 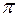-члены

.

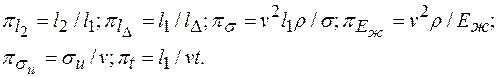Укажем названия и обозначения ряда безразмерных комплексов, отражающих:

поверхностное натяжение - число Вебера

;

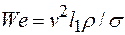упругость жидкости - число Коши

;

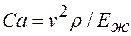время (при неустановившемся движении) - число Струхала

;

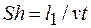турбулентность - число Кармана

.

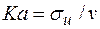Геометрическое соотношение, характеризующее живое сечение, представлено 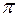-членом .

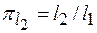Относительная длина элементов (выступов) шероховатости (в направлении движения) представлена 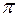-членом .

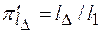Из приведенного перечня факторов, влияющих на потери напора при движении жидкости, конечно, не во всех случаях, могут присутствовать все факторы. В большинстве случаев гидротехнической практики можно не учитывать влияние поверхностного натяжения и сжимаемости. Укажем, что число Коши представляет собой отношение скорости потока к скорости звука в данной жидкости и играет роль в случаях движения, когда скорость 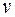сопоставима со скоростью звука.

Найдя 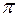-члены, перепишем (5.8) в виде

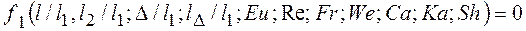(8.7)

и получим уравнение, связывающее 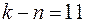безразмерных комплексов.

Учитывая, что 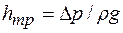и имея в виду расчет потерь напора, выразим число Эйлера как функцию от остальных безразмерных комплексов.

Если движение установившееся, то число Струхала, отражающее влияние неустановившегося характера движения, исчезает (выпадает).

С учетом указанных ограничений имеем

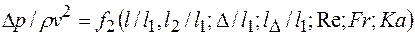. (8.8)

Определение функции 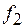является одной из основных задач гидравлики.

Отметим, что безразмерные комплексы - числа Рейнольдса, Фруда, Эйлера и Струхала - можно получить из уравнений Навье - Стокса, приведя их к безразмерному виду.

Иногда в гидравлических исследованиях и расчетах применяют не только выведенные здесь 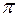-члены, но и их комбинации, например 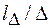, 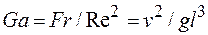- число Галилея и др. Кроме рассмотренных применяются также и другие параметры.

Отметим, что число Рейнольдса характеризует отношение силы инерции к силе вязкости, число Фруда пропорционально отношению силы инерции к силе тяжести, число Эйлера есть отношение силы давления к силе инерции.