Особенности движения жидкой частицы

Теорема Коши-Гельмгольца гласит, что скорость в каждой точке элементарного объема жидкости складывается из скоростей поступательного движения вместе с полюсом, вращательного движения вокруг полюса и деформационного движения (рис. 4.6)

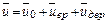. (4.16)

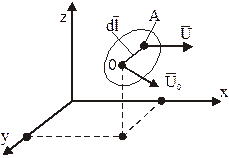
Рис. 4.6. Движение жидкого объема

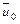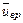Первые два члена и характерны и для движения твердой частицы, поэтому их можно трактовать как скорость квазитвердого движения.

Если положение точки А относительно полюса определяется вектором 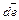, то векторы 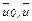и 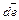имеют компоненты соответственно

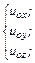
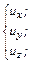
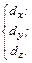(4.17)

Разложение в ряд Тейлора непрерывной функции координат 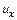с точностью первого порядка малости дает

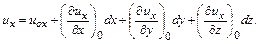(4.18)

Аналогичные соотношения можно получить и для двух других компонентов скорост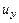и и .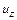

Введем двучлен вида .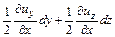

Прибавляя и вычитая его из последнего равенства, запишем

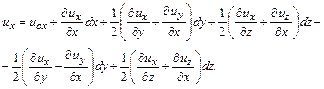(4.19)

Величина 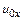характеризует поступательное движение полюса.

Величины

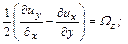
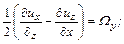
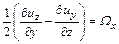
(4.20)

является компонентами угловой скорости вращения частицы вокруг полюса.

Кроме квазитвердого движения частицы происходит деформационное движение ее частей, о чем говорят члены

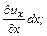
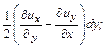
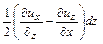. (4.21)

Для пояснения их физического смысла рассмотрим движение отрезка в жидкости 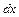вдоль оси 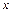(рис. 4.7, а).

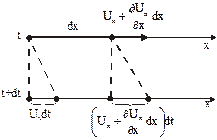
Рис. 4.7 а. Деформация жидкой линии

В момент 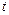скорость начала отрезка 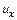.Скорость его конца при разложении по формуле Тейлора будет 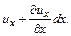За время 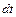отрезок продвигается влево, но его концы пройдут расстояния

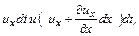(4.22)

то есть отрезок растянется или сожмется.

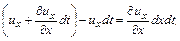(4.23)

т. е. 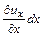есть линейная деформация отрезка за время 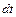или скорость линейной деформации, а 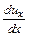является скоростью относительной линейной деформации.

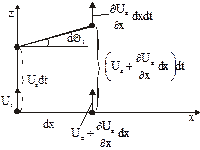
Рис. 4.7б. Деформация жидкой линии

При движении отрезка 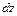вдоль оси 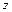(рис. 4.7, б) его концы имеют скорости 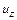и и за время 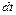пройдут пут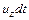и и 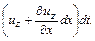В результате за время 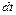отрезок 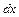повернется на угол

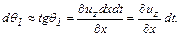(4.24)

Если одновременно движутся два отрезка 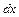и 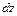, состоящие в начальный момент времени между собой прямой угол. За время 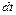повернется на угол 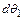, а отрезок 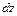на угол .

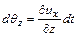Деформация прямого угла равна

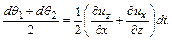(4.25)

скорость деформации прямого угла равна

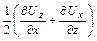(4.26)