Равновесие весомого газа

При больших высотах столба газа величина плотности зависит от высоты. Записав уравнение

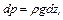(2.33)

введем связь между давлением 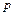и плотностью 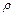. Эта зависимость дается, например законом Бойля-Мариотта, верным при постоянной температуре. По этому закону

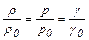. (2.34)

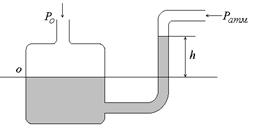
Рис. 2.4. Сообщающиеся сосуды

Подстановка позволяет записать

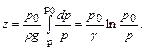(2.35)

Распределение давления имеет вид

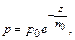(2.36)

где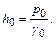

Отсюда следует барометрическая формула для двух высот 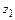и .

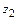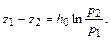(2.37)

Равновесие жидкости

При наличии негравитационных массовых сил

Рассмотрим действие силы инерции (рис.2.6) при движении сосуда с ускорением.

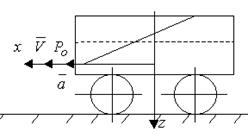
Рис. 2.5. Движение сосуда

Если сосуд движется равноускоренно с ускорением 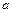, то

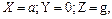(2.38)

поэтому

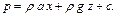(2.39)

пр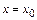и и 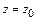давление будет 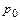, поэтому

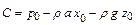. (2.40)

Давление в любой точке жидкости равно

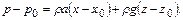(2.41)

Уравнение поверхностей уровней 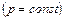имеет вид

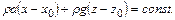(2.42)

При вращении сосуда (рис.2.7) со скоростью 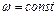проекции сил на оси координат будут

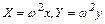и 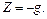(2.43)

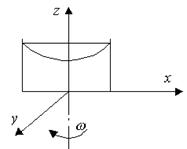
Рис. 2.6. Вращающийся сосуд

Уравнение равновесия имеет вид

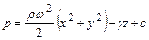(2.44)

пр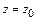и и 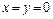получим 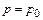, поэтому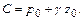

Поэтому гидростатическое давление равно

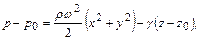(2.45)

и уравнение поверхностей уровня

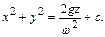(2.46)

Это параболоид вращения.