Гидростатика. Гидростатическое давление

Гидростатика изучает теорию равновесия и относительного покоя жидкостей и газов. Исходным пунктом условий равновесия является изучение сил, действующих на некоторый объем жидкости.

Силы, приложенные к частицам сплошных сред могут быть классифицированы по своей природе или по характеру действия на массовые (объемные) и поверхностные.

В зависимости от области приложения силы подразделяются на внутренние и внешние.

Массовые (объемные) силы пропорциональны массе выделенного объема и действуют на все частицы этого объема. К массовым силам могут быть отнесены силы различного физического происхождения: силы веса, электромагнитные (силы Лоренца, электростатические и силы, действующие на магнитные жидкости) и различные силы инерции (кориолисова сила, центробежная и др.). Это силы дальнодействия.

Поверхностные силы действуют локально на поверхность выделенного объема. В общем случае поверхностные силы могут иметь составляющие, направленные по нормам и по касательной к площадке действия.

В покоящейся жидкости поверхностные силы направлены по нормали поверхности выделенного объема жидкости. В движущейся жидкости дополнительно возникают касательные составляющие поверхностных сил, наиболее важными из которых являются силы трения.

В некотором объеме 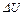распределение массовых сил задается вектором плотности массовых сил 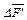, приложенных к частицам этого объема массовой 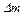при ее стремлении к нулю, т. е.

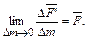(2.1)

Осредненное значение вектора плотности массовых сил равно отношению главного вектора массовых сил к величине массы

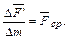(2.2)

Размерность плотности массовой силы совпадает с размерностью ускорения

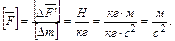(2.3)

Величина поверхностной силы в общем случае зависит от выбора направления элементарной площадки, поэтому обычно рассматривается не сами, а их напряжения

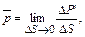(2.4)

где 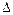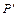главный вектор поверхностных сил, приложенных к площадке .

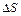Размерность напряжений

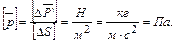(2.5)

В практике используется единица измерения называемая технической атмосферой, которая равна 1 т. а. = 1 кг с/см² = 736 мм рт. ст. = 10 м вод. ст. = 10⁵ Па.

Отметим, что величина 1 Па = 1 бар = 10^{-5 кг с/см2} = 0,1 мм вод. ст.

Рассмотрим равновесие элементарного жидкого объема под действием поверхностных и объемных сил.

Выделим в жидкости элементарный тетраэдр с ребрами 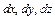(рис.2.2).

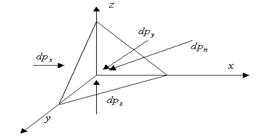
Рис. 2.1. Силы, действующие на элементарный тетраэдр

Обозначим площадки действия элементарных сил соответственно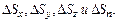

Поверхностные силы элементарного тетраэдра пропорциональны второй степени от размеров тетраэдра, а объемные – третьей и являются величинами третьего порядка малости, тогда как поверхностные имеют второй порядок.

Выделение одной из поверхностей жидкости (рис.2.3) показывает, что в покоящейся жидкости касательная составляющая 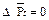и полная величина напряжения или элементарной поверхностной силы равна .

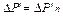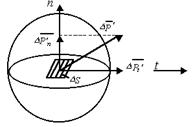
Рис.2.2. Силы, действующие на площадку в жидкости

Для равновесия выделенного объема необходимо, чтобы сумма проекций всех сил на координатные оси была равна нулю:

;

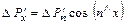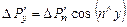; (2.6

,

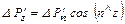где 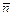- орт нормали к наклонной грани.

Относя величины элементарных сил к площади граней, на которые они действуют, получим

;

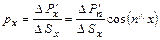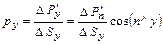; (2.7)

.

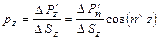Поскольку 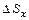, , 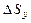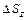являются проекциями наклонной грани на плоскость 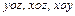, то

;

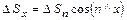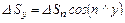; (2.8)

.

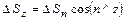Подстановка позволяет записать

;

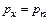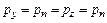или 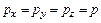. (2.9)

Этот вывод носит название закона Паскаля и гласит, что давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.

Иначе, давление в жидкости, определенное в заданной точке, не зависит от ориентации площадки действия и является функцией только координат

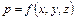. (2.10)

Рассмотрим равновесие элементарного прямоугольного параллелепипеда со сторонами 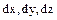, выделенного в покоящейся жидкости.

На единицу массы жидкости действует массовая сила плотностью 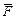с составляющими 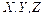. Если от начала координат величина давления является возрастающей функцией координат, а в точке параллелепипеда 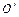действует давление 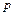, то на соответствующих противоположных гранях давления равны

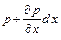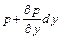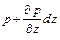; ; . (2.11)

Уравнение равновесия в проекции на ось 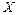имеет вид

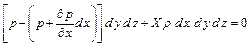(2.12)

или

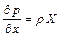. (2.13)

Аналогично, в проекциях на оси координат 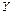и 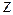получим

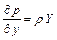; (2.14)

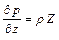. (2.15)

Это уравнения Эйлера или основные уравнения гидростатики.

Эту систему переписывают в виде

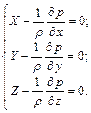(2.16)

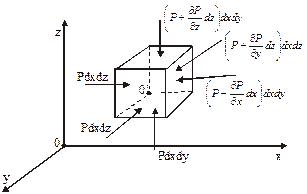
Рис. 2.3.Силы, действующие на элементарный параллепипед

Поскольку

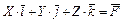(2.17)

и 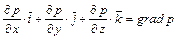, (2.18)

то система может быть переписана в векторной форме

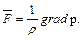(2.19)

Умножая систему уравнений в проекциях последовательно на 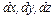и складывая, получим

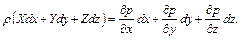(2.20)

Правая часть уравнения является полным дифференциалом, поэтому и левая часть есть полный дифференциал и

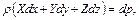(2.21)

где

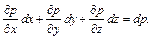(2.22)

в случае изотропной жидкости ( )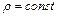

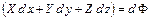, (2.23)

где 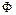- потенциал массовых сил и

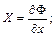
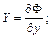
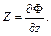(2.24)

В этом случае

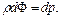(2.25)

Следовательно, жидкость может находиться в равновесии в случае, когда массовые силы, действующие в ней, имеют потенциал.

Поверхность, в каждой точке которой давление постоянно, называется поверхностью уровня. При 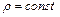уравнение поверхности уровня будет

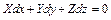(2.26)

или .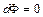

Следовательно, поверхность уровня это одновременно и эквипотенциальная поверхность.

Равновесие тяжелой несжимаемой жидкости.

Для тяжелой несжимаемой жидкости при отсутствии других массовых сил, кроме сил тяжести, имеем

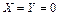и 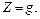(2.27)

поэтому уравнения равновесия принимают вид

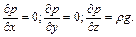(2.28)

Первые два уравнения выражают независимость давления от координат 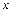и 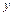, поэтому поверхность уровня являются горизонтальными плоскостями.

Интегрирование последнего уравнения дает при постоянных 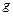и 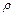выражение

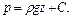(2.29)

Если начало координат совмещено со свободной поверхностью покоящейся жидкости, на которой действует постоянное давление 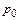, то при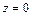

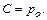
При 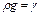получим

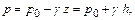(2.30)

где 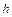- глубина погружения под свободную поверхность, направленная против направления оси .

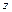Закон гидростатики, следовательно, гласит: давление в любой точке жидкости, находящейся в покое, равно внешнему давлению, сложенному с весом столба жидкости высотой от поверхности до данной точки и с площадью основания, равной единице.

Примером использования основного закона гидростатики является работа сообщающихся сосудов (рис. 2.5.)

Давление в плоскости 0-0 следует считать одинаковым из условия сохранения равновесия жидкости, поэтому

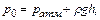(2.31)

что дает

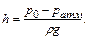(2.32)