Нормальное распределение (НР).
НР особенно часто используется в статистике. Нормальное распределение дает хорошую модель для реальных явлений, в которых:
1. Имеется сильная тенденция данных группироваться вокруг центра;
2. Положительные и отрицательные отклонения от центра равновероятны;
3. Частота отклонений быстро падает, когда отклонение от центра становятся большими;
Механизм, лежащий в основе НР, объясняется с помощью так называемой центральной предельной теоремы, первоначально известной в формулировке Муавра и Лапласа еще в XVII веке как развитие знаменитого закона больших чисел Я.Бернулли (1654-1705, СПб). Сегодня центральная предельная теорема формулируется в принципе инвариантности, идея которого заключается в следующем: при суммировании большого числа независимых величин (например, броуновское движение) получаются именно нормально распределенные величины: смещение при броуновском движении частицы. Иными словами, если на некоторую переменную воздействует множество факторов, эти воздействия независимы, относительно малы и слагаются друг с другом, то получаемая в итоге величина имеет нормальное распределение. Все это происходит независимо, т.е. инвариантно, от распределения исходных величин. Например, практически бесконечное количество факторов определяет вес человека (тысячи генов, предрасположенность, болезни т.д.). Таким образом можно ожидать нормальное распределение веса в популяции всех людей.
Если вы финансист, то Вам, вероятно, известны случаи, когда курсы акций ведут себя подобно броуновским частицам, испытывая хаотические удары многих факторов.
Формально плотность вероятности нормального распределения определяется так:
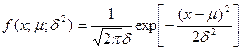
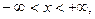
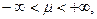
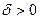
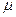 и
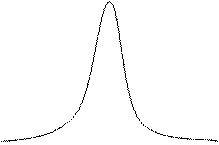
и 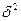 - параметры закона, интерпретируемые как среднее значение и дисперсия данной случайной величины. Визуально график нормальной плотности – это знаменитая колоколообразная кривая:
- параметры закона, интерпретируемые как среднее значение и дисперсия данной случайной величины. Визуально график нормальной плотности – это знаменитая колоколообразная кривая:
 | |||
 | |||
 0.44
0.44
 |
0.33
0.22
0.11
 0.00
0.00
-1 0 1 2 3
Плотность нормального распределения с дисперсией 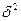 и средним m = 1
и средним m = 1
Соответствующая функция распределения (интегральный закон НР) задается следующим соотношением:
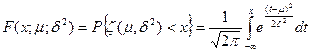
Нормальный закон с параметрами 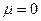 и
и 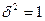 называется стандартным. В соответствии со свойствами функции распределения:
называется стандартным. В соответствии со свойствами функции распределения:
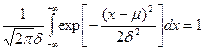
При практических расчетах используют нормированную случайную величину:
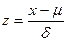 , которая имеет функцию плотности
, которая имеет функцию плотности 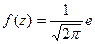 - это и есть стандартный нормальный закон.
- это и есть стандартный нормальный закон.
Обратная функция стандартного нормального распределения, примененная к величине Z, 0<Z<1, называется пробит-преобразованием Z, или просто пробитом Z.
Основные характеристики нормального закона (НЗ):
Среднее, мода, медиана: 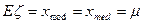
Дисперсия: 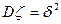
Асимметрия: 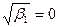
Иногда стандартное отклонение называют среднеквадратическим отклонением, но это уже устаревшая терминология.
В программных пакетах (SPSS, Statistika, MatLab…) используется обозначение:
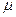 - mean – среднее
- mean – среднее
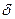 - standart deviation – стандартное отклонение
- standart deviation – стандартное отклонение
Вычисление вероятности попадания значений случайной величины, распределенной по НЗ, в заданный интервал, определяется с помощью табулированных значений интеграла Гаусса:
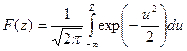 , причем
, причем 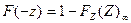
(Доказательство: 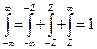 ,
, 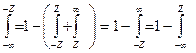 )
)
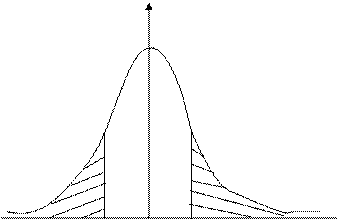
Вероятность попадания Х в интервал [X1, X2] равна:
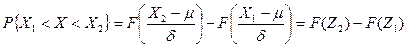 , что иллюстрируется графически так:
, что иллюстрируется графически так:
 F(z)
F(z) 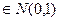
 F(z
F(z 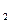 )=P
)=P 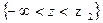
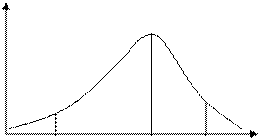 F(x)
F(x) 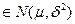

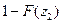
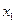

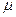
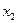 x
x
z 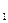 z
z 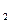
 z=
z= 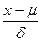
При статистической обработке данных число использует двух-( 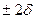 ) и трёхсигмовые (
) и трёхсигмовые ( 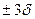 ) пределы отклонения случайной величины от центра распределения
) пределы отклонения случайной величины от центра распределения 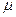 , вероятности которых равны соответственно:
, вероятности которых равны соответственно:
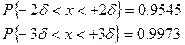
Рассмотрим моменты случайной величины, распределённой по H3:
Первый начальный момент, или математическое ожидание:
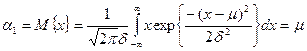
Центральные моменты S-го порядка
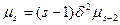
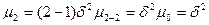
Нулевой центральный момент 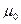 .
.

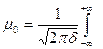 eхр
eхр 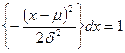

 Первый центральный момент:
Первый центральный момент:

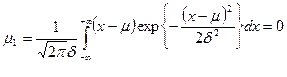


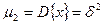

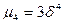

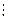

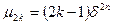
 Все
Все 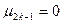
 Таким образом, в HP:
Таким образом, в HP:

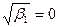 -асимметрия
-асимметрия

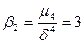 -эксцесс.
-эксцесс.
 Практические задания:
Практические задания:
 Задание1: Функция распределения N(0,1)
Задание1: Функция распределения N(0,1)
 Вычисление y=P(x)=P{X<=x}-вероятность.
Вычисление y=P(x)=P{X<=x}-вероятность.
 где X-HP случайная величина с
где X-HP случайная величина с 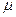 =0 и
=0 и 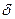 =1
=1
 (нулевое среднее) (единичная дисперсия)
(нулевое среднее) (единичная дисперсия)
P(x)= 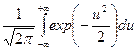
При вычислениях использовать чебышевскую аппроксимацию:
P(x)=1-f(x) 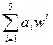 , x>=0
, x>=0
Где w= 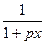
f(x)= 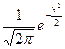
p=0.2316419
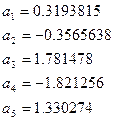

Мах ошибка аппроксимации равна 7* 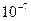
Указание:а)применять схему Горнера
б)при выходе из процедуры выдавать f(х)-плоскость(строить график).
Задание2: Моделировать HP случайную величину с заданным средним (М) и стандартным отклонением(S):
y= 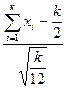 , где
, где
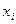 -равномерно распределённое случайное число на
-равномерно распределённое случайное число на  0<
0< 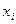 <1
<1
Y аппроксимирует точное HP при к 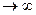 если к=12, то y=
если к=12, то y= 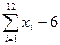
Переход к требуемому среднему и стандартному отклонению осуществлять по формуле:
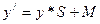
\ /
заданы!
Задание3. Генерировать 100,1000,10000 случайных величин с H3 и строить гистограмму.
Убедиться в справедливости правила 2-и 3-сигма, которое имеет следующий смысл:
если от точки среднего или что то же самое, от точки максимума плотности HP отложить вправо и влево соответственно два и три стандартных отклонения
(2- и 3-сигма) , то площадь под графиком нормальной плотности , подсчитанная по этому графику , будет соответственно равна 95,45% и 99,73% всей площади под графиком .
Другими словами , это можно выразить следующим образом:95,45% и 99,73% всех
независимых наблюдений из нормальной совокупности, например размеров детали
или цены акций, лежат в зоне 2- и 3-стандартных отклонений от среднего значения.
Дата добавления: 2018-06-28; просмотров: 637;
