Глава 6. Концентрация напряжений

Общие положения

В сварных соединениях распределение напряжений неравномерно - имеет место их концентрация, то есть образование значительных напряжений на участках малой протяжённости.

Рассмотрим распределение напряжений в пределах упругих деформаций в полосе шириной а, ослабленной круглым небольшим отверстием диаметром d (рис.6.1 а).

Нормальные напряжения в поперечном сечении А—А(рис.6.1 а) определяются формулой

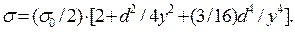(6.1)
При у = d/2 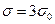т.е. теоретический коэффициент концентрации напряжений 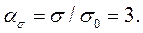При у = 2d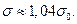

В случае эллиптического отверстия (рис. 1.6 б) коэффициент концентрации напряжений в пределах упругих деформаций

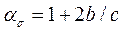. (6.2)

При 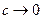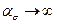. Это решение не точно, так как при малых значениях с деформации, вызванные внешними силами, оказывают существенное влияние на форму отверстия и формула (6.2) не выполняется.

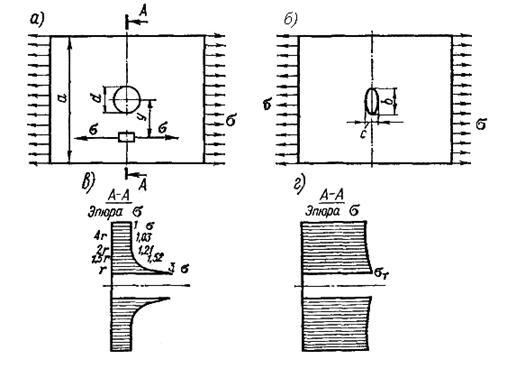
Рис. 6.1. Концентрация напряжений:

а — в полосе с круглым отверстием; б — в полосе с эллиптическим отверстием; в — распределение σ в упругой стадии; г — распределе­ние σ в пластической стадии нагружения

Указанные местные напряжения в зоне концентрации не опасны для прочности в конструкциях из пластичных металлов при ста­тических нагрузках. Поясним это положение.

Диаграммы растяжения пластичного металла нередко схемати­зируются. Их приближенно заменяют двумя прямыми: наклонной, выражающей зависимость напряжения от деформации в упругой области, и горизонтальной (рис.6.2).

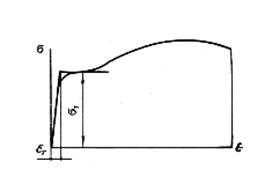
Рис.6.2. Диаграмма растяжения пластичного металла

Горизонтальная прямая показывает, что при ε>ε_т деформация протекает пластически, без увеличе­ния нагрузки, приложенной к испытуемому элементу.

Вернемся к рассмотрению эпюры напряженной полосы, ослаб­ленной отверстием (рис. 6.1 в). Напряженное состояние в сечении А–А близко к одноосному. Допустим, что около отверстия напряжение σдостигло значения σ_т. Это соответствует деформа­ции ε_т. При увеличении нагрузки деформации возросли, но напря­жения в зоне, где ε>ε_т, как это следует из схематизированной диаграммы растяжения, остаются равными σ_т. Эпюра станет изме­нять свою форму и выравниваться. Приближенно можно принять, что она примет очертание, близкое к прямоугольному (рис. 6.1 г), что и было положено в основу расчета прочности по элементарным формулам.

Сглаживание эпюры напряжений в пластической стадии, рассмотренное на конкретном примере, является закономерным про­цессом, имеющим место во многих элементах конструкций из пластичных сталей (низкоуглеродистых и низколегированных) при одноосных напряженных состояниях (а иногда и многоосных). Однако концентрация напряжений существенно снижает прочность при переменных нагрузках, а в случае ограниченной пластично­сти металла — и при статических нагрузках.

Концентрацию напряжений в сварных конструкциях вызывают следующие причины.

Технологические дефекты шва— газовые пузыри, шлаковые включения и особенно трещины и непровары. Возле этих дефектов при нагружении силовые линии искривляются, в результате чего образуется концентрация напряжений. Коэффициенты концентра­ции напряжений около указанных дефектов значительны, но при их небольшом числе и размерах прочность сварных соединений остается удовлетворительной. В плотных однородных стыковых швах концентрация напряжений может быть сведена до минимума. Нерациональные очертания швов.На основании данных теории упругости установлено, что очертание швов оказывает большое влияние на распределение в них внутренних сил. На металличе­ских моделях и на моделях из прозрачного материала эти данные экспериментально подтверждены.

Нерациональные конструкции соединений(примеры нерацио­нальной конструкции соединений рассмотрены в следующих пара­графах этой главы).