Простые ставки ссудных процентов

Простые ставки ссудных (декурсивных) процентов применяют­ся обычно в краткосрочных финансовых операциях, когда интер­вал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Есте­ственно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в опера­ции сторон.

Введем следующие обозначения:

i(%) — простая годовая ставка ссудного процента;

ния;

Р — величина первоначальной денежной суммы;

S — наращенная сумма;

п — продолжительность периода начисления в годах;

д — продолжительность периода начисления в днях;

К — продолжительность года в днях. Величина К являетсявременной базой для расчета процентов.

В зависимости от способа определения продолжительности фи­нансовой оперции рассчитывается либо точный, либо обыкновен­ный (коммерческий) процент.

.

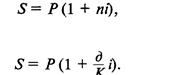
Простые учетные ставки

При антисипативном способе начисления процентов сумма по­лучаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (т. е. из наращенной сум­мы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называ­етсядисконтированием по учетной ставке, а такжекоммерческимилибанковским учетом.

Дисконтом называется доход, полученный по учетной ставке, т. е. разница между размером кредита и непосредственно выдавае­мой суммой. Пусть теперь (/(%) — простая годовая учетная ставка;

d — относительная величина учетной ставки;

S — сумма, которая должна быть возвращена;

Р — сумма, получаемая заемщиком.

Тогда, согласно определениям, получаем формулу для опре­деления наращенной суммы:

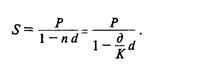
Пример

Кредит выдается на полгода по простой учетной ставке 40%. Рассчитать сумму, получаемую заемщиком, и величину дисконта, если требуется возвратить 30 000 000 руб.

РешениеПо формуле (2.5) получаем:

Р = 30 000 000 (1 - 0,5 • 0,4) = 24 000 000 руб. Далее:

Д = S - Р = 30 000 000 - 24 000 000 = 6 000 000 руб.

Сложные ставки ссудных процентов

Если после очередного интервала начисления доход (т. е. на­численные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют фор­мулы сложных процентов. Сложные ссудные проценты в настоя­щее время являются весьма распространенным видом применяе­мых в различных финансовых операциях процентных ставок.

Основная формула расчета сложного ссудного процента

S=P*(1+i)ⁿ

Это основная формула проента применяемая в финансовых расчетах.

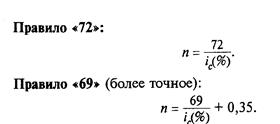
Эти правила позволяют определить за какой срок n вложенный капитал увеличится в 2 раза при известной ставке процента i (которая выражается в процентах, а не в долях единицы) Данные правила дают весьма точный результат, отклонения достаточно малы и ими можно пренебречь.

Особые случаи расчета сложного процента

1. Когда в периоде начисления содержится нецелое число интервалов. Например, при ежегодном начислении процента кредит выдается на нецелое число лет

Тогда при расчете по основной формуле мы получим погрешность при возведении в дробную степень.Точный расчет осуществляют по следующей формуле

S=P*(1+i)^na*(1+in_b)

Здесь n_a – целое число интервалов

n_b - дробный остаток интервала.

Например, если кредит выдан на 3,5 года при ежегодном начислении процента то n_a = 3, n_b = 0,5

Фактически формула является комбинацией сложного процента (первая скобка) и простого процента (вторая скобка). То есть мы рассчитываем сложный процент за целое число интервалов, а затем рассчитываем простой процент за дробный остаток интервала от всей накопленной суммы

2. Когда процент начисляется несколько раз за временную единицу, в которой выражена ставка процента. Напрмер, дана годовая ставка процента, а процент начисляется раз в полгода, квартал или раз в месяц.

В этом случае формула приобретет следующий вид:

S=P*(1+i/m)^n*m

m – количество интервалов начисления в той временной единице, в которой выражена ставка процента

Например, ставка процента годовая. Тогда это количество интервалов начисления в году, то есть сколько раз за год начисляется процент. Если процент начисляется раз в полгода то m=2 (то есть 2 раз за год), если процент начисляется раз в квартал то m=4 (4 раз за год), если процент начисляется раз в месяц то m=12 (12 раз за год) и т.д.