Төртбұрышқа іштей және сырттай сызылған шеңбер
Егер төртбұрыштың барлық төбелері қандай да бір шеңбер бойында жатса, төртбұрыш шеңберге іштей сызылған деп аталады. Ал, егер төртбұрыштың барлық қабырғалары қандай да бір шеңберге жанама болса, оны шеңберге сырттай сызылған деп атайды.
Теорема1) Егер төртбұрышқа шеңберге сырттай сызылған болса,онда төртбұрыштың қарама-қарсы жатқан бұрыштардың қосындысы 1800-ға тең болады.
2)Егер төртбұрыштың қарама-қарсы екі бұрышының қосындысы 180°-қа тең болса, онда бұл төртбұрышты сырттай шеңбер сызуға болады.
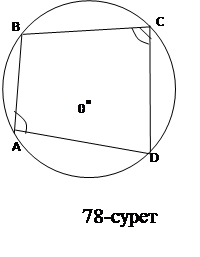
Салдар Кез-келген тіктөртбұрышқа сырттай шеңбер сызуға болады.Сырттай сызылған шеңбер радиусы 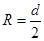 ,мұндағы
,мұндағы 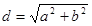 -тіктөртбұрыштың диагоналі,
-тіктөртбұрыштың диагоналі, 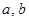 -қабырғалары.
-қабырғалары.
Салдар Квадратқа сырттай шеңбер сызуға болады.Сырттай сызылған шеңбер радиусы 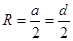 ,мұндағы
,мұндағы 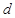 -квадраттың диагоналі,
-квадраттың диагоналі, 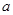 -қабырғасы.
-қабырғасы.
Салдар Трапецияға сырттай шеңбер сызуға болады сонда тек сонда ғана, егер ол теңбүйірлі трапеция болса, және, керісінше, егер трапецияға сырттай шеңбер сызылса, онда бұл трапеция теңбүйірлі.
Салдар Шеңберге іштей сызылған төртбұрыш
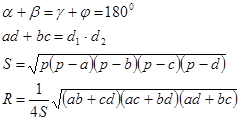
бұл жерде а,в,с,d-іштей сызылған төртбұрыштың қабырғалары, 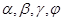 -төртбұрыштың бұрыштары,R-сырттай сызылған шеңбердің радиусы.
-төртбұрыштың бұрыштары,R-сырттай сызылған шеңбердің радиусы.
Шеңбер сызып, оның бойынан төрт нүкте белгілейік те, осы нүктелер арқылы шеңберге жанамалар жүргізейік. Жанамалардың өзара қиылысу нүктелері арқылы төртбұрыш пайда болады. Сонда төртбұрышқа іштей сызылған шеңбер шығады. Төртбұрыштың ішкі бұрыштары шеңберге іштей сызылған болады да, ал қабырғалары сәйкес кесінділері тең болатын шеңбердің жанамалары.
Теорема 1) Егер де төртбұрышқа іштей шеңбер сызуға болса, онда төртбұрыштың қарама-қарсы қабырғаларының 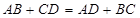 қосындысы тең болады.
қосындысы тең болады.
2) Егер де төртбұрыштың қарама-қарсы қабырғаларының 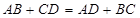 қосындысы тең болса, бұл төртбұрышқа іштей шеңбер сызуға болады.
қосындысы тең болса, бұл төртбұрышқа іштей шеңбер сызуға болады.
Салдар Кез-келген ромбыға іштей шеңбер сызуға болады.Іштей сызылған шеңбердің радиусы келесі шарттарды қанағаттандырады:
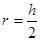 , мұндағы
, мұндағы 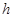 -ромб биіктігі:
-ромб биіктігі:
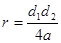 ,мұндағы
,мұндағы 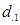 және
және 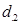 -ромбының диаметрлері.
-ромбының диаметрлері.
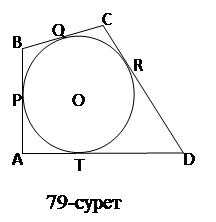
Салдар Шеңберге сырттай сызылған төртбұрыш үшін
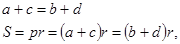
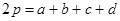
бұл жерде а,в,с,d-cырттай сызылған төртбұрыштың қабырғалары,r-іштей сызылған шеңбердің радиусы.
Мысал Табандары 8 см және 2 см-ге тең болатын тең бүйірлі трапецияға іштей шеңбер сызылған. Шеңбердің ұзындығын табыңыз.
Берілгені: 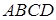 -тең бүйірлі трапеция,
-тең бүйірлі трапеция, 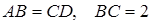 см,
см, 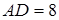 см.
см.
 Табу керек:
Табу керек: 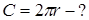
Шешуі: 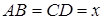 болсын.
болсын.
Шеңбер трапецияға іштей сызылғандықтан,
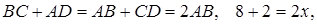
бұдан 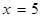 см,
см, 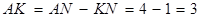
болатындықтан, 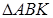 -нан:
-нан:
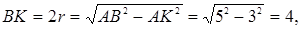
бұдан 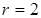 . 80-сурет
. 80-сурет
Демек, трапецияға іштей сызылған шеңбердің ұзындығы 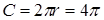 см-ге тең.
см-ге тең.
Жауабы: 4 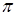 см.
см.
 Мысал Радиусы
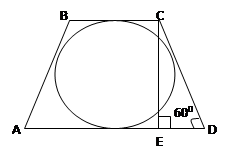
Мысал Радиусы 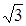 -ке тең дөңгелекке сүйір бұрышы 600-қа тең болатын тең бүйірлі трапеция сырттай сызылған. Трапецияның орта сызығының ұзындығын табыңыз.
-ке тең дөңгелекке сүйір бұрышы 600-қа тең болатын тең бүйірлі трапеция сырттай сызылған. Трапецияның орта сызығының ұзындығын табыңыз.
Берілгені:  -тең бүйірлі трапеция.
-тең бүйірлі трапеция. 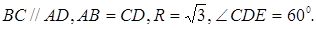
Табу керек: 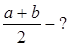
Шешуі: 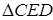 -нан:
-нан: 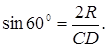 81-сурет
81-сурет
Осыдан 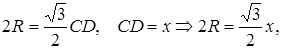
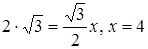 .
.
Шеңбер трапецияға іштей сызылғандықтан, 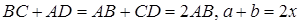 , бұдан
, бұдан 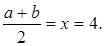
Демек, трапецияның орта сызығы 4-ке тең.
Жауабы: 4.
Мысал Тең бүйірлі трапецияның периметрі оған іштей сызылған шеңбердің ұзындығынан екі есе үлкен. Трапецияның табанындағы бұрышты табыңыз.
Берілгені: 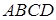 -тең бүйірлі трапеция,
-тең бүйірлі трапеция, 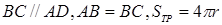 .
.
Табу керек: 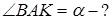
Шешуі: 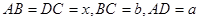 деп белгілейік. Есептің шарты бойынша
деп белгілейік. Есептің шарты бойынша 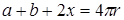 .
.
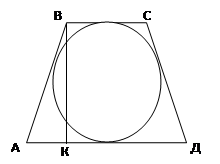 Трапеция шеңберге сырттай сызылғандықтан,
Трапеция шеңберге сырттай сызылғандықтан,
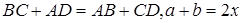 болады,
болады,
сондықтан 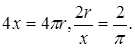
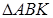 -нан:
-нан: 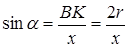 , бұдан
, бұдан
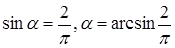 . 82-сурет
. 82-сурет
Демек, ізделінді бұрыш 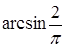 -ге тең.
-ге тең.
Жауабы: 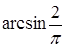 .
.
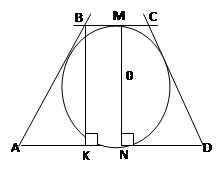
Мысал Тең бүйірлі трапецияның табан қабырғаларының ұзындықтары 21 және 9-ға, ал биіктігі 8-ге тең. Трапецияға сырттай сызылған шеңбердің радиусын табыңыз.
Берілгені: 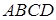 -тең бүйірлі трапеция,
-тең бүйірлі трапеция, 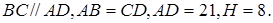
Табу керек: 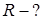
Шешуі: 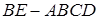 трапецияның биіктігі болсын,
трапецияның биіктігі болсын, 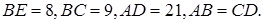
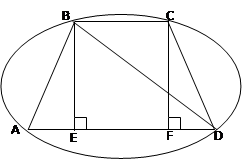 Сонда
Сонда 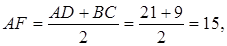
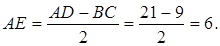
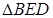 -нан:
-нан:
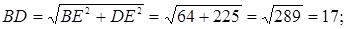
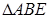 -нан: 83-сурет
-нан: 83-сурет
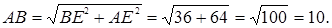
ABCD трапецияға сырттай сызылған шеңбердің радиусы 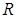 -ді,
-ді, 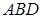 үшбұрышына сырттай сызылған дөңгелектің радиусы ретінде анықтаймыз
үшбұрышына сырттай сызылған дөңгелектің радиусы ретінде анықтаймыз 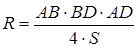 . Үшбұрышты жарты периметрі
. Үшбұрышты жарты периметрі 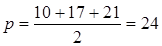 -ке, ал ауданы
-ке, ал ауданы 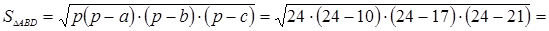
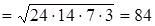 -ке тең. Бұдан
-ке тең. Бұдан 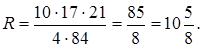
Трапецияға сырттай сызылған шеңбердің радиусы 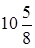 -ге тең.
-ге тең.
Жауабы: 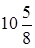 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| КРИЗИС ЕВРОПЕЙСКОЙ ЦИВИЛИЗАЦИИ И КУЛЬТУРЫ НА СОВРЕМЕННОМ ЭТАПЕ | | | Степень свободы конструкции |
Дата добавления: 2018-03-01; просмотров: 39557;
