Задача Эйлера для отдельно работающих балок

Рассмотрим решение задачи устойчивости упругого стержня, постоянного поперечного сечения, расположенной на двух шарнирно опертых концах, при действии продольной силы переменной величины Р (рис.13.2).Впервые эта задача была поставлена и решена Л. Эйлером в середине XVIII века.

На начальном этапе действия постоянно возрастающей силы Р, очевидно, что в поперечных сечениях стержня возникают только продольно сжимающие силы и стержень испытывает сжатие, сохраняя прямолинейную форму деформированного состояния (1). Считая данную форму деформированного состояния в качестве начальной, предполагают, что при некотором значении внешней силы Р = Pкр стержень изогнется, т.е. в некотором новом равновесном состоянии принимает искривленную форму (2), изображенную на рис.

Обозначая величину прогибов стержня через y (z) в сечении, расположенном на расстоянии z от начала системы координат y z, значения изгибающих моментов в указанном поперечном сечении от действия внешней силы Р принимают значения

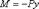
Из теории изгиба, при малых прогибах и пренебрегая продольными деформациями, деформированное состояние стержня за счет изгиба, описывается уравнением

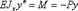(13.1)

Принимая обозначение

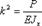(13.2)

уравнение (13.1) можно представить в следующем виде:

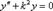(13.3)

Решение (13.3) имеет следующий вид:

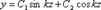(13.4)

Произвольные постоянные С1 и С2 определяются из граничных условий закрепления балки, т.е. y(0) = 0; y(l) = 0. Из первого условия вытекает, что С2 = 0, а из второго

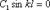(13.5)

Последнее уравнение имеет два возможных решения: либо С1 = 0, либо же .

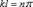В первом случае получается, что С1 = С2 = 0 и перемещения согласно (13.4) тождественно равны нулю, т.е. y = 0. Это решение очевидно соответствует первоначальному равновесному состоянию, которое нас не интересует. Во втором случае, т.е. предполагая, что С1 ¹ 0, из (13.5) следует, что Откуда следует, что , где n = 1,2,3,... С учетом выражения (13.2), получим 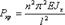. Наименьшая критическая сила 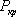получается при n=1:

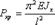(13.6)

Эта сила носит название первой критической или эйлеровой силы. Решение (4.4) при С1 ¹ 0 C2 = 0 принимает вид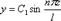

При выполнении практических расчетов, как правило, определяется критическое значение внешней силы, соответствующее низшей форме потери устойчивости системы. Поэтому мы далее будем рассматривать решение задачи по определению только наименьшего значения критических сил.

4. Модифицированный метод перемещений расчета сжато-изогнутых элементов в рамах.Предположим, что все элементы заданной системы изначально имеют прямолинейную форму и сопряжены между собой под пря­мым углом. В данном случае при действии узловых нагрузок на­чальная форма равновесного состояния системы соответствует докритической стадии работы конструкций, в поперечных сечениях элементов системы возникают только продольные силы и они ра­ботают либо на сжатие, либо на растяжение. Как и для обычных стержней, продольными деформациями оси элементов заданной системы пренебрегаем. Принимая, что рассматриваемая рамная система с произвольным п раз кинематически неопределимой системой (n = 1, 2, 3,...), ка­нонические уравнения метода перемещений для нового равно­весного, т.е. критического состояния, как и в классическом методе перемещений записывается в форме

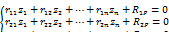
При расчетах на устойчивость система преобразуется. Так как мы рассматриваем только случай действия узловых нагрузок, то во введенных связях они никакой реакции не вызывают. То есть в данном случае следует принимать

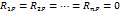
Единичные реакции r_ik (i_,k = 1, 2, 3,..., п), как и при расчете обычных статических задач, определяются из условия равновесия узлов или отдельных частей основной системы при заданных еди­ничных смещениях. В узловых сечениях элементов значения моментов и поперечных сил в общем случае являются функциями от параметра внешних продольных сил v. Следовательно, и единичные реактив­ные усилия во введенных связях r_ik в общем случае являются функ­циями от параметра v и обозначаются r_ik (v).

С учетом выше изложенного система преобразуется и за­писывается следующим образом:

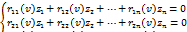
Так как в новом равновесном (критическом) состоянии, состав­ные элементы искривляются, следовательно, все неизвестные Zi за­ведомо не могут быть равны нулю. Поэтому определитель одно­родной системы алгебраических уравнений , составленный из коэффициентов при неизвестных, должен быть равен нулю

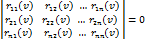
Раскрыв определитель и приравняв его нулю, получим трансцендентное уравнение относительно параметра критической нагрузки v. Решив это уравнение относительно v и по минималь­ному значению корня v = v_min, определяют критическое значение внешних сил.

5. Алгоритм расчета (ебаный вопрос если честно, я пишу со своих слов)

1) рисуем основную систему метода перемещений. В местах, где приложена вертикальная сила, номеруем стояки(?)

2) Строим по таблицам М1 и М2

3) записываем каноническую систему, находим r11, r12, r22

4) записываем определитель устойчивости. Упрощенный вид Δ=r₁₁*r₂₂ – r₁₂*r₂₁=0

5) находим параметр v. 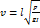. Из найденных значений v, выбираем большее.

6) подставляем найденное v в определитель.

7) рисуем таблицу. В шапку выписываем слогаемые из определителя.

8) задаемся v, выписываем для них значения из таблицы(v, φ). В итоге выбираем значение v, при котором наш определитель будет равен(близко приближен) к нулю.

9) находим P_крит. P_крит=v²*EI\l². v- найденное значение методом интерполяции из таблицы.

Определение критической силы и приведенной длины для сжато-изогнутых балок в состоянии бифуркации

Для составления расчетной схемы надо построить и проанализировать эпюру продольных сил в заданной системе.

Идея метода перемещения в заданной устойчивости, система разбивается на отдельные элементы, путем ведения фиктивных связей. Затем записывается система канонических уравнений. т.к. в данных расчетных схемах нагрузка всегда узловая, то грузовая эпюра моментов и грузовые коэффициенты системы уравнений всегда равны нулю. В задачах устойчивости система канонических уравнений всегда однородны.

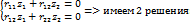
Либо z_i=0; либо не нулево решение, когда определитель составлен из коэффициентов системы (r_ij)=0.

При потере устойчивости сжатого элемента узлы обязательно перемещаются. В сжатых элементах эпюры моментов будут криволинейно-тригонометричны, в зависимости от критического параметра . После раскрытия определителя получается сложное трансцендентное уравнение, которое легко решается графическим методом или методом подбора. В общем случае уравнение даст несколько корней, истинный тот, который наименьший. Определяем v=> определяем коэффециент μ=π/v => приведенная длина l₀= μ*l.

Расчетная длина – это длина полуволны синусоиды, по которой изгибается сжатый элемент, потерявший устойчивость.

F_крит=v²EI/l²