Элементы математической логики. 2 страница
ВЫРАЖЕНИЕ ОДНИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
1. Функция f 8(x1,x2) = x1®x2 (импликация x1 в x2) может быть записана посредством функций дизъюнкции и отрицания
x1>x2=  Úx 2.
Úx 2.
Доказательство осуществляется посредством таблиц истинности.
| x 1 | x 2 | x1®x2 |
| x1 | x2 |  
|  Ú x 2 Ú x 2
|
2. Функцию эквивалентности f7(x1,x2)=x1~x2 = x1ºx2 выразим посредством других функций x1~x2= (  Úx2)&(x 1Ú
Úx2)&(x 1Ú 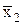 )
)
| x 1 | x 2 | x1~x2 | ||||
| x 1 | x 2 | 
| 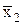
|  Úx 2 Úx 2
| x1Ú 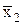
| (  Úx2)&(x 1Ú Úx2)&(x 1Ú 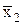 ) )
|
3. f 11(x1,x2) = x1  x2=
x2= 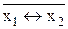
| x 1 | x 2 | x1  x2 x2
| x1~x2 | 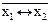
|
или
f (x1,x2) = x1  x2=(
x2=(  & x2)
& x2)  (x1&
(x1& 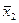 )
)
| x 1 | x 2 | x1  x2 x2
| 
| (  &x2) &x2)
| 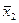
| (x1& 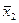 ) )
| (  &x2) &x2)  (x1& (x1& 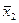 ) )
|
4. 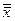 =x
=x
| x | 
| 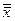
|
5. x1& x2= 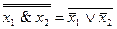
| x 1 | x 2 | x1& x2 |
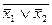
| x 1 | x 2 | 
| 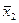
|   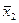
| 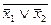
|
6. x1  x2=
x2= 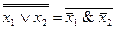
| x 1 | x 2 | x1  x2 x2
|
| x 1 | x 2 | 
| 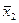
|  & & 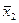
| 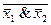
|
7. x1  x2=
x2= 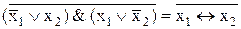
| x 1 | x 2 | x1  x2 x2
|
| x 1 | x 2 | 
| 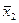
|   x2 x2
| x1  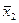
| 
|
Свойства конъюнкции, дизъюнкции и отрицания
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются сочетательный
x1&(x2&x3)= (x1&x2)&x3,
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3,
x3,
переместительный
x1  x2= x1
x2= x1  x2,
x2,
x1& x2= x1&x2,
и распределительный законы. Кроме того, выполняется распределительный закон дизъюнкции относительно конъюнкции.
x1  (x2&x3)= (x1
(x2&x3)= (x1  x2)& (x1
x2)& (x1  x3).
x3).
Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.
| x 1 | x 2 | x 3 | x2&x3 | x1  (x2&x3) (x2&x3)
|
| x 1 | x 2 | x 3 | x1  x2 x2
| x1  x3 x3
| (x1  x2)& (x1 x2)& (x1  x3) x3)
|
Совпадение построенных таблиц доказывает наше утверждение.
Рассмотрим теперь ряд простых, но весьма важных соотношений
 х
х  х=х;
х=х;
х&х=х.
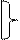 х
х  1=1; х
1=1; х  0=х; х
0=х; х 
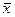 =1;
=1;
х&1=х. х&0=0. х& 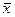 =0.
=0.
И как следствие получаем
х  х
х  …
…  х=х,
х=х,
х&х&…&х=х.
Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана
х1  х2
х2  …
…  хn=
хn=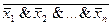 ;
;
х1&х2&…&хn=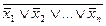 .
.
Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба)
Свойства функции сложения по модулю 2 и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств.
Для функции сложения по модулю 2 выполняются переместительный и сочетательный законы, а также распределительный закон относительно конъюнкции:
x1 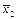 x2= x2
x2= x2  x1;
x1;
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3;
x3;
x1&(x2  x3)= (x1&x2)
x3)= (x1&x2)  ( x1&x3).
( x1&x3).
Справедливы также очевидные соотношения
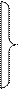 x
x  x=0;
x=0;
x  0=х;
0=х;
x  1=
1= 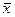 ;
;
х 
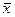 =1.
=1.
Кроме того, выполняется формула х1  х2= x1
х2= x1  x2
x2  x1&x2.
x1&x2.
В отличие от всех ранее рассмотренных функций для импликации не выполняются переместительный и сочетательный законы, однако справедливы следующие соотношения:
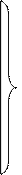 х®x=1;
х®x=1;
x® 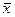 =
= 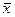 ;
;
x®1=1;
х®0= 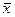 ;
;
0®х=1;
1®х=х;
х1®х2= 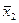 ®
® 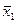 ;
;
х1®х2® х1= х1.
Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:
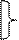 х1
х1  х2=
х2= 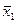 ® х2;
® х2;
х1&х2= 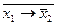 .
.
Для функции Шеффера и Вебба справедлив переместительный закон:
х1 /х2= х2/х1;
х1¯х2= х2¯х1.
Сочетательный закон для них не выполняется:
х1/(х2/х3)¹(х1/х2)/х3 ;
х1¯( х2¯х3)¹ (х1¯ х2)¯ х3.
 Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:
Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:
х /х= 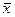 , х¯ х=
, х¯ х= 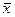 ;
;
х/ 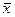 =1, х¯
=1, х¯ 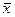 =0;
=0;
х/1= 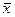 , х¯1 =0;
, х¯1 =0;
х/0=1, х¯0= 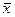 ;
;
х1/х2= 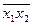 =
= 

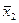 ;
;
х1¯х2= 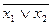 =
=  &
& 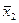 .
.
Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулами де Моргана для функций конъюнкции и дизъюнкции:
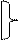 х1/х2=
х1/х2=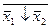 ;
;
х1¯х2=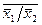 .
.
ОСНОВНЫЕ КЛАССЫ ФАЛ
В качестве первого класса таких ФАЛ рассмотрим класс функций, сохраняющих константу нуль, т.е. таких функций, для которых справедливо равенство
f (0, 0, …, 0)=0
Очевидно, что в фиксированном множестве число функций этого класса составляет половину всех функций алгебры логики, т.е. 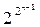 функций.
функций.
Аналогично класс функций, сохраняющих константу единица, будет определен, как класс функций, для которых выполняется равенство
f (1, 1,…, 1)=1
Этот класс состоит также из 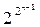 функций.
функций.
Определение Функция f*(x1 ,…,xn) называется двойственной к функции f (x1 ,…,xn), если выполняется равенство
f*(x1 ,…,xn)= 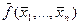 .
.
Определение Функция . f (x1 ,…,xn) самодвойственный, если она совпадает с двойственной себе функцией, т.е. справедливо равенство
f (x1 ,…,xn )= 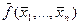 .
.
Определение ФАЛ f(x1,…,xn ) называется линейной, если она представима в следующем виде
f (x1 ,…,xn )=с0  с1х1
с1х1  …
…  сnхn,
сnхn,
где коэффициент сi 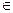 {0, 1}.
{0, 1}.
Число членов этого класса 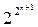 .
.
Определение ФАЛ f(x1,…,xn ) называется монотонной, если для любых двух наборов Х1 и Х2 таких, что Х1³ Х2 выполняется равенство
f (X1)³f (X2)
X1=< 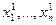 >
>
X2=< 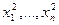 >.
>.
Определение ФАЛ f(x1,…,xn ) называется симметричной, если она не изменяется при произвольной перенумерации аргументов.
f(x1,…,xn )= f(y1,…,yn ),
где (y1,…,yn) – любая перестановка аргументов (x1,…,xn ).
АНАЛИТИЧЕСКАЯ ЗАПИСЬ ФАЛ
Пусть имеется двоичный набор < 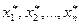 >. Сопоставим ему число i, определяемое
>. Сопоставим ему число i, определяемое
i= 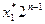 +
+ 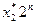 +…+
+…+ 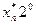 ,
,
число i называют номером набора < 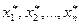 >.
>.
Рассмотрим функцию F(x1,…,xn), определяемую следующим соотношением
 1, если номер набора i
1, если номер набора i
(0) Fi=
0, в противном случае.
Такую функцию называют характеристической функцией «единицы». Предположим, что удалось построить аналитическое выражение для функции Fi (как это можно сделать описывается ниже). Тогда справедлива следующая теорема.
Дата добавления: 2017-11-04; просмотров: 545;
