Элементы математической логики. 1 страница
Математическая логика – раздел науки, истоки которого восходят к Аристотелю (384 -322 г. до н. э.). Как математическая дисциплина начала формироваться в середине XIX в., благодаря работам английского логика и математика Дж. Буля (1815-1864).
Целью логики является анализ методов рассуждений, при этом логика, прежде всего, интересуется формой, а не содержанием рассуждений, то есть выясняет, следует истинность заключения из истинности посылок. Это время характеризовано кризисом в физике, обусловленным ломкой старых представлений о материальном объекте, не учитывающих, что всякий материальный объект неисчерпаем по своим свойствам; кризисом в математике, обусловленных открытием порядков, то - есть рассуждений, приводящих к противоречиям. Известны и логические парадоксы.
1. Примером множеств являются множество всех студентов группы, множество преподавателей, множество всех людей. Объекты, из которых состоит множество, называются его элементами. Множество могут быть и элементами множеств. Например, множество студенческих групп в качестве элементов содержит множество студентов отдельных групп. Большинство множеств не являются элементами самих себя. Например, множество всех людей не являются элементом себя, так как само не человек. Однако множество всех множеств – элемент самого себя.
Рассмотрим теперь множество А всех таких множеств Х, что Х не есть элемент х. Согласно определению, если А есть элемент А, то А также и не есть элемент А, а если А не есть элемент А, то А есть элемент А. В любом случае А есть элемент А и А не есть элемент А. Этот парадокс открыт Б. Расселом в 1902г.
Семантический парадокс «лжеца» таков.
Некоторое лицо говорит: «Высказывание, которое я сейчас произнесу, ложно». Стоящее в кавычках высказывание не может быть без противоречия ни истинным, ни ложным. Этот парадокс был хорошо известен в древности (парадокс Эвбулида – IV в. до н.э.).
Так как логические рассуждения составляют скелет всей математики и теория множеств лежит в ее основе, то парадоксы побудили математиков к поиску решения проблем и были предложены различные аксиоматические теории.
Главная цель применение в логике математической символики заключалась в том, чтобы свести операции с логическими заключениями к формальным действиям над символами. При этом исходные положения записываются формулами, которые преобразуются по определенным законам, а полученные результаты истолковываются в соответствующих понятиях.
Логика нашла энергичные применение в вычислительной технике в теории преобразовании и передачи информации, в экономике, биологии, психологии и т.д.
Математическая логика разделяется на ряд отдельных разделов: двузначная, многозначная, пороговая, непрерывная, нечеткая, порядковая логики.
Объектом математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.
ПОНЯТИЕ ВЫСКАЗЫВАНИЯ
В логике под высказыванием понимают предложение, относительно которого можно сказать, истинно оно или ложно в настоящее время.
Примеры: 1.Дон впадает в Азовское море. 2.Два больше трех. 3.Я лгу.
Первые два предложения являются высказываниями, первое из них – истинно, второе – ложно. Третье предложение не является высказыванием. Допустим, что это предложение истинно тогда в силу его смысла, оно должно быть ложным. Аналогично, из ложности этого предложения вытекает его истинность.
В алгебре высказываний не рассматривают внутреннюю структуру и содержание высказываний, а ограничиваются рассмотрением их свойства представляет истину или ложь.
Из высказываний путем соединения их различными способами можно составлять новые, более сложные высказывания. Для образования таких комбинаций будем использовать логические операции, основные из которых вводятся следующим образом.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Пусть даны два произвольных высказывания А и В.
1. Выражение АΛВ означает высказывание, истинное только тогда, когда А и В истинны. Такое высказывание называется конъюнкцией высказывания А и В. Символ Λ означает операцию, называемую конъюнкцией. В обычной речи этой операции соответствует соединение высказываний союзом «И», «А», «ДА». Будем считать, что если А, В истинны, то они соответственно принимают значение 1, ложно – 0.
Таблица истинности данной операции имеет вид Λ?&
| А | В | АΛВ |
Логические операции называются конъюнкцией.
2. Выражение А  В означает высказывание, истинное, когда, по крайне мере одно из высказывание А или В истинно.
В означает высказывание, истинное, когда, по крайне мере одно из высказывание А или В истинно.
Такое высказывание называется дизъюнкцией высказываний А и В. Символ  означает операцию, называемой дизъюнкцией. В обычной речи этой операции соответствует соединение высказыванием связкой «ИЛИ».
означает операцию, называемой дизъюнкцией. В обычной речи этой операции соответствует соединение высказыванием связкой «ИЛИ».
Таблица истинности
| А | В | А  В В
|
3. Выражение А>В означает высказывание, которое ложно тогда и только тогда, когда А истинно, а В ложно. Такое высказывание называется импликацией высказываний А и В. Символ > означает операцию, называемую импликацией. Читается «А влечет В» или «если А, то В»
Таблица истинности (А>В) = ( 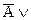 В)
В)
| А | В | А>В |
4. Выражение А~В означает высказывание, которое истинно тогда и только тогда, когда А и В оба истинны, или оба ложны. Такое высказывание называется эквивалентностью. В обычной речи этой операции соответствует соединение высказывания «тогда и только тогда, когда». (АВ 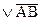 ) = А~В
) = А~В
| А | В | А~В |
5. Выражение А означает высказывание, которое истинно, когда А ложно и ложно, когда А – истинно.
Такое высказывание называется отрицательным высказыванием А. Черточка над буквой означает операцию, называемую отрицанием. В обычной речи этой операции соответствует образование нового высказывания с помощью частицы НЕ.
| А | В |
6. Операцией неравнозначности (равноименности) высказываний А,В называют составное высказывание, обозначаемое АВ, которое истинно тогда и только тогда, когда значение истинности высказываний А,В противоположны и ложно в противном случае, что отражается таблицей истинности
| А | В | А  В В
|
В составленном высказывании порядок выполнения логических операций определяется круглыми скобками, а при их отсутствии сначала выполняется отрицание, а затем конъюнкция, далее дизъюнкция, а потом все остальное. При отсутствии скобок порядок операции совпадает с порядком их перечисления.
Например, определим значение истинности составного высказывания
D=А&(А&В> 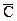 )
) 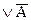 &В
&В
при А=0, В=1, С=1
А&В=0, А&В>С=1
А&(А&В>С)=0
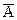 &В=1, D=1.
&В=1, D=1.
Рассмотрим обратную задачу. Пусть D=0. Необходимо найти хотя бы один набор значение высказываний А, В, С, при которых D=0.
В составленном высказывании «D» последней логической операции является дизъюнкция, поэтому составные высказывания
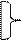 А&(А&В>С)=0
А&(А&В>С)=0
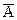 &В=0.
&В=0.
Для того чтобы
А&(А&В> 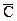 )=0 , необходимо чтобы или А=0 , или (А&В>
)=0 , необходимо чтобы или А=0 , или (А&В> 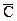 )=0
)=0
Рассмотрим случай, когда
(А&В> 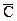 )=0.
)=0.
Последней операцией здесь является импликация, равная 0 в единственном случае, когда (А&В)=1, а 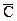 =0. Отсюда имеем С=1, А=1, В=1. Ясно, что при А=1, В=1 составное высказывание
=0. Отсюда имеем С=1, А=1, В=1. Ясно, что при А=1, В=1 составное высказывание 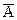 &В=0. Таким образом требуемый набор значений А, В, С определен.
&В=0. Таким образом требуемый набор значений А, В, С определен.
ЛОГИЧЕСКИЕ ФУНКЦИИ.
Отличительной особенностью логических функций состоит в том, что они принимают значения в конечных множествах. Иначе говоря, область значений логической функции всегда представляет собой конечную совокупность чисел, символов, понятий, свойств и, вообще, любых объектов.
Если область значений функций содержит k различных элементов, то она называется k-значной функцией.
Переименуем элементы области значений функции числами 1, …,k (или обозначают буквами). Перечет всех символов, соответствующих области значений, называют алфавитом, а сами символы - буквами этого алфавита(латинского, русского или другого алфавита, порядковые числа или любые другие символы).
Логические функции могут зависеть от одной, двух и любого числа переменных (аргументов) х1, …, хn.
В теоретико-множественном смысле логические функции n переменных y=f(x1, …, xn) представляет собой отображение множества наборов (n-мерных векторов, кортежей последовательностей) вида (х1, х2, …, хn) являющегося областью ее определения, на множество ее значений.
Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией.
Логическую функцию можно также рассматривать как операцию, заданную законом композиции
Х1 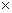 Х2
Х2 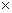 …
… 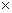 Хn>N, где Х1, …, Хn – множества, на которых определены аргументы
Хn>N, где Х1, …, Хn – множества, на которых определены аргументы
х1 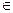 Х1 , х2
Х1 , х2 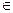 Х2 , …, хn
Х2 , …, хn 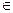 Хn .
Хn .
Если Х1= Х2=…= Хn=N, и однородная функция, рассматриваемая как закон композиции
Nn>N, определяет n-местную операцию на конечном множестве N.
Областью определения однородной функции y=f(x1, x2, …, xn) служит множество наборов (х1, …, хn), называемых словами, где каждый из аргументов х1, х2, …, хn заменяется буквами k-ичного алфавита (0,1, ..., (k-1)). Количество n букв в данном слове определяет его длину.
Очевидно, число всевозможных слов длины n в k-ичном алфавите равно kn. Так как каждому такому слову имеется возможность представить одно из k значений множества N, то общее количество однородных функций от n переменных выражается числом 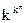 .
.
Если буквами алфавита служат числа от 0 до (k-1), то каждое слово (х1, х2, …, хn) символически представляется упорядоченной последовательностью n таких чисел и рассматривается как запись n-разрядного числа в позиционной системе счисления с основанием k, то есть
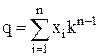
или х1kn-1+ х2kn-2+…+ хn-1k1+ хnk0=q.
Числа q=0,1,…,kn-1 служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность. Аналогично номерами функций можно считать kn разрядные числа в той же системе счисления.
Различны слова длины n в данном алфавите образуется как n-перестановки с повторениями.
Так в трехзначном алфавите (0,1,2) словами длины 4 будут всех четырехразрядные числа с основанием k=3, т.е. 0000, 0001,0002,0010, 0011, …, 2221, 2222 которые соответствуют десятичным числам от 0 до 80=2•33+2•32+2•31+2•30.
Поставить каждому такому числу в соответствии одну из букв алфавита {0,1,2}, получим некоторую функцию четырех переменных
f(x1, x2, x3, x4),
причем количество таких функций выразится числом 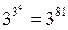 .
.
Наиболее простым и важнейшим классом однородных функций являются двузначные (булевы) функции (иногда ее называют переключательной). Функция f(x1, x2, …, xn-1, xn) принимает два значения 0,1 и зависит от переменных xi 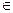 {0,1}, i=
{0,1}, i= 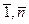 .
.
Областью определения булевой функции служит совокупность всевозможных n-мерных наборов из 0 и 1, а для ее задания достаточно указать, какие значения функции соответствуют каждому из этих наборов, т.е. осуществить табличные значения функции.
| x1, x2, …, xn-1, xn | f (x1, x2, …, xn-1, xn) |
| 0 0 … 0 0 | f (0 , 0 , …, 0 , 0) |
| 0 0 … 0 1 | f (0 , 0 , …, 0 , 1) |
| … … … … … | … … …… … … … |
| 1 1 … 1 0 | f (1 , 1 , …, 1 , 0) |
| 1 1 … 1 1 | f (1 , 1 , …, 1 , 1) |
Каждому набору α=(α1, …,αn) αi 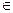 {0,1} становится в соответствии число
{0,1} становится в соответствии число
N=α12n-1+…+ αn-12+ αn.
Наборам (0, 0, …, 0, 0), (0, 0, …, 0, 1), …, (1, 1, …, 1, 1) соответствуют числа 0,1, …, 2n-1.
Легко видеть, что число n-мерных наборов из 0 и 1 равно 2n.
Если зафиксировать n переменных x1, x2, …, xn , то разные функции от переменных x1, x2, …, xn задаются разными таблицами. Число различных таблиц равно числу всех функций от переменных x1, x2, …, xn. Число булевых функций от n переменных x1, x2, …, xn равно 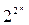 .
.
Познакомимся с другими способами задания булевой функции.
Сначала познакомимся с функцией одной и двух переменных, которые иногда называют «элементарными» функциями».
ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ И ИХ ОСНОВНЫЕ СВОЙСТВА.
Рассмотрим множество векторов 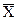 ={ x1, x2, …, xn }, пусть координаты этих векторов принимают значения 0 или 1. Таким образом, множество Х состоит из 2n различных векторов.
={ x1, x2, …, xn }, пусть координаты этих векторов принимают значения 0 или 1. Таким образом, множество Х состоит из 2n различных векторов.
Совокупность координат некоторого фиксированного вектора 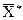 из множества
из множества 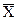 будем называть двоичным набором или просто набором.
будем называть двоичным набором или просто набором.
Сопоставим каждому вектору Х число 0 или 1, т.е. произведем однозначное отображение Х на множество Y={0,1}.
ФУНКЦИЕЙ АЛГЕБРЫ ЛОГИКИ
ФАЛ называется функция, дающая однозначное отображение Х в Y.
1. Число различных ФАЛ, зависящих от n аргументов, конечно и равно 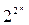 .
.
| x1, x2, …, xn-1, xn | f (x1, x2, …, xn-1, xn) |
| 0 0 … 0 0 | α1 |
| 0 0 … 0 1 | α2 |
| … … … … … | … … …… … … … |
| 1 1 … 1 0 | 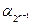
|
| 1 1 … 1 1 | 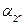
|
Если наборам значений аргументов ФАЛ сопоставляет точки n- мерного пространства, то множество 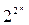 наборов определяет множество вершин n- мерного единичного куба. Таким образом, областью определения ФАЛ, зависящей от n аргументов, является множество вершин такого куба.
наборов определяет множество вершин n- мерного единичного куба. Таким образом, областью определения ФАЛ, зависящей от n аргументов, является множество вершин такого куба.
Пример.
ФАЛ f(x1, x2, x3) может быть задана геометрически . f(101, 110, 010, 011)=1

|
Значения ФАЛ могут быть заданы не на всех возможных наборах аргументов. На некоторых значения функции могут быть не определены. Такие функции называют не полностью определенными.
2. Если две ФАЛ f1(x1, x2, …, xn-1, xn) и f2(x1, x2, …, xn-1, xn) принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f1 и f2 называются равными.
3. ФАЛ f(x1, x2, …, xi, xi+1, …, xn-1, xn) существенно зависит от аргумента xi, если имеет место соотношение
f(x1, x2, …, xi-1,0 , xi+1, …, xn-1, xn)¹ f(x1, x2, …, xi-1,1 , xi+1, …, xn-1, xn)
в противном случае говорят, что от xi функция зависит не существенно и xi является ее фиктивным аргументом. ФАЛ не изменяется, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными.
Как найти несущественные аргументы? Для этого, если ФАЛ задана таблично, поступают следующим образом.
Разбивают множество наборов аргументов функции на два подмножества:
- подмножество, на котором заданная функция принимает значение 1;
- подмножество, на котором заданная функция принимает 0.
Для проверки фиктивности аргумента xi вычеркивают столбец, ему соответствующий, и проверяют, не появились ли в обоих подмножествах одинаковые наборы. Если таких наборов не появилось, то xi является фиктивным аргументом.
Пример:
Таблица
| x1 x2 x3 x4 | f (x1, x2, x3, x4) |
| 0 0 0 0 | |
| 0 0 0 1 | |
| 0 0 1 0 | |
| 0 0 1 1 | |
| 0 1 0 0 | |
| 0 1 0 1 | |
| 0 1 1 0 | |
| 0 1 1 1 | |
| 1 0 0 0 | |
| 1 0 0 1 | |
| 1 0 1 0 | |
| 1 0 1 1 | |
| 1 1 0 0 | |
| 1 1 0 1 | |
| 1 1 1 0 | |
| 1 1 1 1 |
Произведем разбиение набора аргументов:
x1 x2 x3 x4
 0 0 0 0
0 0 0 0
0 0 0 1 x1 x2 x3 x4
 0 0 1 0 0 1 0 0
0 0 1 0 0 1 0 0
0 0 1 1 наборы х 0 1 0 1
0 1 1 0 на которых 1 1 0 0 f( 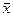 )=1
)=1
0 1 1 1 f( 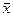 )=0 1 1 0 1
)=0 1 1 0 1
1 0 0 0 1 1 1 0
1 0 0 1 1 1 1 1
1 0 1 1
Вычеркнем в наборах четвертый столбец. Оставшиеся наборы таковы, что ни один из них не входит одновременно в оба подмножества. Это свидетельствует о фиктивности аргумента x4.
Элементарные функции алгебры логики
Рассмотрим множество элементарных ФАЛ. Начнем со случая, когда длина слова n=0. По формуле, определяющей число функций логики, вычисляем, что при n=0 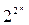 = 2.
= 2.
f1=0; f2=1.
Эти две функции совпадают с константами.
В случае n=1 мы имеем две функции, существенно зависящие от аргумента x, эти две функции определяются таблицей
| x1 | f 3 | f 4 |
Эти две функции также относят к элементарным, и они записываются следующим образом
f 3=x ; f 4= 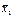 (читается «не x»).
(читается «не x»).
Функцию f 4 называют функцией отрицания.
В случае n=2 имеем десять различных функций, существенно зависящих от аргументов x1 и x2.
| x1Úx2 | x1&x2 | x1~x2 | x1®x2 | x1 ¯ x2 | x1/x2 | x1  x2 x2
| ||
| x 1 | x 2 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 |
Функция f5(x1,x2) =x1Úx2 (дизъюнкция).
Функция f6(x1,x2) =x1&x2 (конъюнкция).
Вместо символов & часто применяют символ умножения «•» или вообще опускают также, как и в обычной алгебре.
Функция f7 носит название функции эквивалентности или функции равнозначности
f7(x1,x2) = x1~x2
и f7(x1,x2) = x1ºx2.
Функция f8 носит название импликации x1 в x2. Она обозначается f8(x1,x2) = x1®x2.
Функция f9 носит название функции Вебба (или ее называют еще стрелкой Пирса) и обозначается
f 9(x1,x2) = x1vx2.
Функция f9 называется функцией (штрихом) Шеффера и обозначается следующим образом f 10(x1,x2) = x1 ¯ x2.
Функция f 11 обычно называется функцией сложения по модулю 2.
f 11(x1,x2) = x1 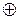 x2.
x2.
Рассмотрение одиннадцати функций позволяют строить новые функции двумя основными способами:
1. путем перенумерации аргументов;
2. путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f 1, f 2, f 3, …, f k путем применения этих правил будем называть суперпозицией функции f 1, f 2, f 3, …, f k .
Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить следующие новые функции ФАЛ.
Используя таблицы, определяющие элементарные функции, можно задать любую функцию ФАЛ, являющуюся суперпозицией этих функций.
Пример. Пусть требуется представить в виде таблицы следующую функцию
f (x1,x2,x3)={[(  ~x2)Ú (x1 ¯ x2)] (x1
~x2)Ú (x1 ¯ x2)] (x1  x2)}®x3.
x2)}®x3.
Будем строить ФАЛ последовательно.
| x1 | x2 | x3 | 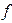 
|  ~x2 ~x2
| x1¯x2 | [ ] | x1Úx2 | { } | f (x1,x2,x3) |
Дата добавления: 2017-11-04; просмотров: 835;
