Элементы теории наивыгоднейшего расположения осветительных приборов
Расположение светильников общего освещения оказывает влияние на экономичность, качество освещения и удобство эксплуатации.
На рис. показано расположение светильников относительно основных поверхностей в помещении, где приняты обозначения, которые в дальнейшем будут использоваться.
| H |
| h |
| hp |
| hc |
| hп |
| L |
| l |
где H – высота помещения, hc – высота свеса светильников, hр – высота рабочей поверхности над полом, hп – высота установки СП над полом, h – расчетная высота, L – расстояние между светильниками или их рядами, l – расстояние крайних рядов СП от стены.
Размеры H и hp являются заданными, hc принимается в пределах от 0 до 1,5м. Расстояние l рекомендуется принимать около 0,5L при наличии проходов у стен, и 0,33L в остальных случаях. В случае необходимости обеспечить у стен такую же освещенность, как и по всей площади, допускается уменьшать l почти до нуля. Классическим считается размещение светильников по вершинам прямоугольных полей, при этом желательно чтобы La:Lb не превышало 1,5. Также используется шахматное расположение СП по вершинам ромбов с острым углом 600. Следует по возможности избегать однорядного расположения СП. СП с трубчатыми люминесцентными лампами размещают рядами желательно параллельно стене с окнами или длинной стороне узкого помещения, это обеспечивает направление света близкое к естественному, позволяет включать в сумерках освещение только в глубине помещения и уменьшает протяженность групповой сети.
Нормированные значения освещенности в помещении должны быть достигнуты наивыгоднейшим образом. Для решения светотехнической задачи необходимо по возможности обеспечить минимум светового потока, минимум мощности или минимум эксплуатационных годовых затрат. Соответственно этому различают светотехнически наивыгоднейшее расположение, энергетически наивыгоднейшее расположение и экономически наивыгоднейшее расположение. Для нахождения наивыгоднейшего расположения находят оптимальное соотношение расстояния между светильниками к расчетной высоте: 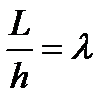
Рассмотрим задачу определения наивыгоднейшей высоты подвеса одиночного светильника, освещающего точку А горизонтальной поверхности, удаленную на расстояние d от проекции светильника на эту поверхность (рис.)
s 02088VKPXQ5z1ZF90gjbW3W6G2z9geD/O1nOlGL5WsIu71VWvGsob/uWK8MGKcw5nus5a0fKTN/H QbPW0ZeH2D5PR68ouQ3mr05/hx8K5DlW5SuqQ7fypOzyNcrLR4P3/gMAAP//AwBQSwMEFAAGAAgA AAAhAEuYuTDdAAAABQEAAA8AAABkcnMvZG93bnJldi54bWxMj8FuwjAQRO+V+g/WVuqlKk6hEJTG QVXVcugN6AFuxl6SCHsd2Q6Ev6/ppVxWGs1o5m25GKxhJ/ShdSTgZZQBQ1JOt1QL+Nl8Pc+BhShJ S+MIBVwwwKK6vytlod2ZVnhax5qlEgqFFNDE2BWcB9WglWHkOqTkHZy3Mibpa669PKdya/g4y2bc ypbSQiM7/GhQHde9FZDvLsvvrfHxOFVPh8/ehQ0aJcTjw/D+BiziEP/DcMVP6FAlpr3rSQdmBKRH 4t9N3utkPgG2FzDOZznwquS39NUvAAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAAT AAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/W AAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAOFHSiRL BgAAYiwAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAEuY uTDdAAAABQEAAA8AAAAAAAAAAAAAAAAApQgAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMA AACvCQAAAAA= ">
| n |
| α |
| d |
| h |
| I(α) |
| A |
Обычно для простоты в ручных расчетах принимается, что светораспределение светильника подчиняется закону:
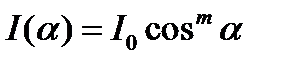 где m = 1,2,3…
где m = 1,2,3…
Справедливость такого допущения иллюстрируется рис.
Очевидно, что данная зависимость хорошо описывает равномерное светораспределение (m=0), косинусное светораспределение (m=1), глубокое и концентрированное (m>1).
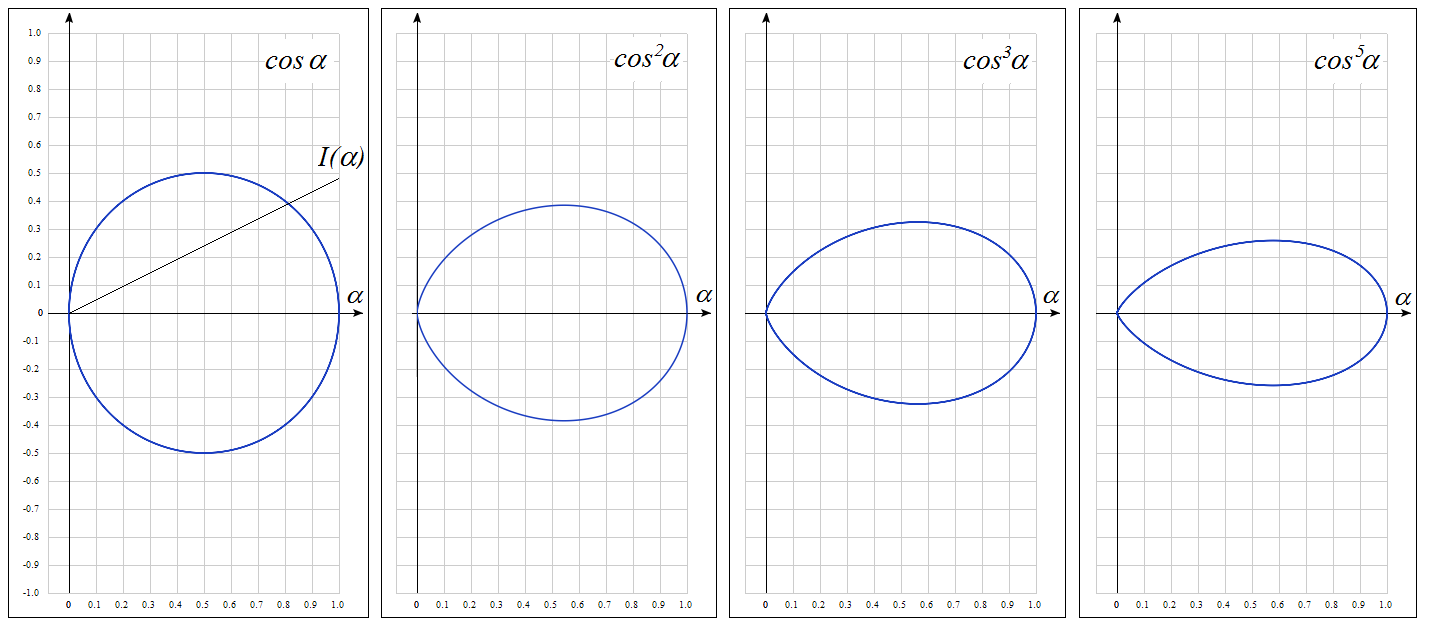
Функция cosmα в полярной системе координат при различных значениях параметра m
Запишем выражение для освещенности от одиночного точечного источника:
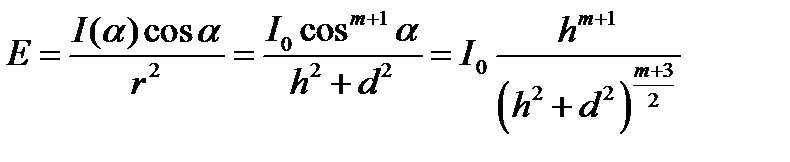
Находя первую производную освещенности по высоте и приравнивая её к нулю получим значение наивыгоднейшей высоты:
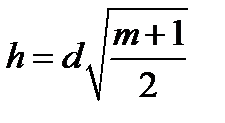
В случае расположения СП по вершинам квадратных полей
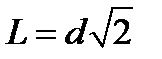 откуда имеем:
откуда имеем:
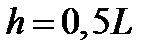 - для равномерного светораспределения (m=0)
- для равномерного светораспределения (m=0)
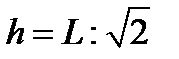 - для косинусного светораспределения (m=1)
- для косинусного светораспределения (m=1)
При заданном световом потоке СП светотехническая экономичность может быть принята пропорциональной полезному потоку, который в случае квадратных полей определяется из условия:
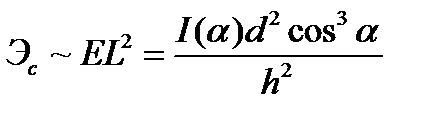
откуда
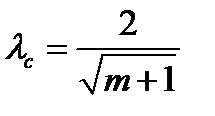
данное соотношение справедливо также для светящих линий.
Условия электрической экономичности определяются максимумом функции:
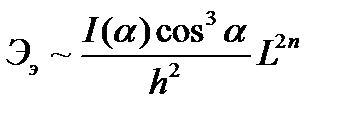 где n ≈ 1,14
где n ≈ 1,14
откуда
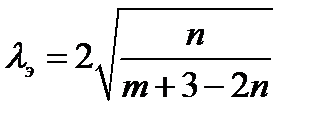
Дата добавления: 2017-11-04; просмотров: 926;
