Лекция №16. Функции пользователя. Структура функций
Если результатом подпрограммы является только одно значение, то такую подпрограмму можно оформить в виде функции. Функция пользователя аналогична процедуре с той лишь разницей, что:
Функция передает в программу результат своей работы – единственное значение, носителем которого является имя самой функции;
Имя функции может входить в выражение как операнд. Функция возвращает результат в точку своего вызова.
Функция, определенная пользователем, имеет заголовок и тело. Заголовок содержит зарезервированное слово function, имяфункции,заключенный в круглые скобкинеобязательныйсписокформальных параметрови – в отличие от процедуры, типвозвращаемого функцией значения:
FunctionИмяФункции[(ФормальныеПараметры)]: ТипРезультата;
Например:
Function func1(n: integer): integer;
Function func2(a,b: real): real;
Function func3: integer;
Имя функции уникально в пределах одной программы.
Тело функции аналогично по своей структуре обычной программе.
В разделе операторов функции должен находиться хотя бы один оператор, который присваивает ее имени значение, возвращаемое как результат работы функции. Если таких присваиваний несколько, то результатом выполнения функции будет значение последнего оператора присваивания. Если же такого оператора нет, то значение, возвращаемое функцией, не определено.
В отличие от процедуры, вызов функции не оформляется в виде отдельного оператора. Обращение к функции осуществляется путем использования указателя функции в качестве операнда в некотором выражении. Указатель функции – это ее имя со списком аргументов, т.е. фактических параметров.
Например: writeln(func1(i));
c:= func2(2,5);
Writeln(func3);
Таким образом, общий вид описания функции следующий:
Function Имя[(Список формальных параметров)]: Тип результата;
{Описательная часть}
Begin
Тело функции, в котором обязательно
долен быть оператор присваивания
Имя функции:= значение;
End;
Пример 1
Составить программу, подсчитывающую число сочетаний без повторения из n элементов по k.
Число сочетаний без повторения вычисляется по формуле: 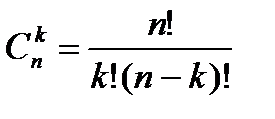
Решение
Обозначим через n и k переменные для хранения введенных чисел; c − переменную для хранения результата.
Чтобы подсчитать количество сочетаний без повторения, необходимо вычислить n!, (n-k)!, k!
Опишем функцию для вычисления факториала числа
n(n!= 1•2•...•n).
{заголовок функции}
Function factorial(n:Integer):Longint;
{описательная часть}
Vari: Integer;
rez: Longint;
{тело функции}
Begin
rez:=1;
For i:=1 To n Do rez:=rez*i;
factorial:=rez; {присваивание значения имени функции}
End;
Первая строчка в описании функции − это ее заголовок. Служебное слово Function (функция) указывает на то, что именем factorial названа функция. В скобках записан список формальных параметров функции, состоящий из одной переменной целого типа. Далее в заголовке указан тип значения функции. В данном примере результат функции factorial − длинное целое число.
За заголовком функции следует описательная часть функции, которая, как и у программы, может состоять из разделов описания переменных, констант, типов. В данном примере имеется только раздел описания переменных. В нем описаны переменные i (счетчик цикла) и rez (для накопления значения факториала).
Далее идет раздел операторов (тело функции). Результат присваивается имени функции, таким образом функция получает свое значение.
В тексте программы описания функций всегда следуют за разделом описания переменных и до начала основной части, как и описания процедур. После того как функция описана, ее можно использовать в программе.
Дата добавления: 2017-11-04; просмотров: 1385;
