Правила оформления схем алгоритмов. Разновидности структур алгоритмов
По структуре алгоритмы разделяют на линейные, разветвляющиеся и циклические.
Линейными называют алгоритмы, в которых операции выполняются последовательно одна за другой, в естественном и единственном порядке следования.
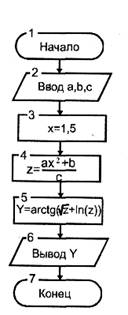
Рис.1. Схема линейного алгоритма.
Пример 1.Найти значение функции при значении аргумента x=1,5 и заданных а, b, с.
Алгоритмы, в которых в зависимости от выполнения некоторого логического условия происходит разветвление вычислений по одному из нескольких возможных направлений, называют разветвляющимися.Подобные алгоритмы предусматривают выбор одного из альтернативных путей продолжения вычислений. Каждое возможное направление вычислений называется ветвью.
Пример 2. Даны два числа а и b.
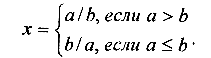
Найти
Очевидно, что для определения ветви , по которому необходимо производить процесс вычисления значения х, достаточно проверить выполнение одного из условий, например а>b. Если условие а>b не выполняется, то очевидно и без дополнительной проверки, что будет выполнено условие а < b. Следовательно, вариант схемы алгоритма будет выглядеть следующим образом
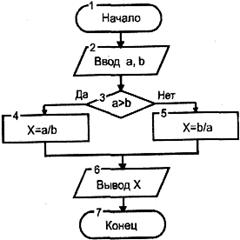
Рис.2. Схема разветвляющегося алгоритма.
Алгоритм циклическойструктуры предусматривает многократное повторение действий в одной и той же последовательности по одним и тем же математическим зависимостям, но при разных значениях некоторой специально изменяемой величины. Циклические алгоритмы позволяют существенно сократить объем программы за счет многократного выполнения группы повторяющихся вычислений, так называемого тела цикла. Специально изменяемый по заданному закону параметр, входящий в тело цикла, называется переменной цикла.Переменная цикла используется для подготовки очередного повторения цикла и отслеживания условий его окончания. Во время выполнения тела цикла параметры переменной цикла изменяются в интервале от начального до конечного значения с заданным шагом. Следовательно, при организации циклических вычислений необходимо предусмотреть задание начального значения переменной цикла, закон ее изменения перед каждым новым повторением и ее конечное значение, при достижении которого произойдет завершение цикла.
Циклы, в теле которых нет разветвлений и других встроенных в них циклов, называют простыми. В противном случае их относят к сложным. Циклические алгоритмы разделяют на детерминированные и итерационные.
Циклы, в которых число повторений заранее известно из исходных данных или определено в ходе решения задачи, называют детерминированными. Для организации детерминированных циклов наиболее целесообразно использовать блок модификации, внутри которого указывается переменная цикла, ее начальное и конечное значения, а также шаг ее изменения . Организовать подобный цикл возможно и при использовании блока проверки условия вместо блока модификации. Циклы, в которых число повторений неизвестно из исходных данных и не определено по ходу решения задачи, называют итерационными. В итерационных циклах для организации выхода из тела цикла предусматривается проверка некоторого заранее заданного условия, для чего используют блок проверки условия. В итерационных циклах невозможно использовать блоки модификации, так как при организации таких циклов заранее неизвестно количество изменений переменной цикла и ее конечное значение.
В зависимости от местонахождения блока проверки условия итерационные циклы могут быть организованы как циклы с предусловием (блок проверки условия размещен перед телом цикла) или с постусловием (блок проверки условия размещен после тела цикла). Если в цикле с предусловием входящие в тело цикла команды могут не выполняться ни разу (если начальное значение параметра цикла удовлетворяет условию выхода из цикла), то в цикле с постусловием - выполняются как минимум один раз (даже если начальное значение параметра цикла удовлетворяет условию выхода из него).
Пример 3.Дано натуральное число N. Найти сумму первых N членов натурального ряда.
Варианты схемы алгоритма циклической структуры решения поставленной задачи приведены на рис.3.1. и рис.3.2. При этом в схеме на рис. 3.1. цикл организован с использованием блока модификации, а на рис. 3.2. - блока проверки условия. В обоих алгоритмах операция нахождения суммы, при предварительном обнулении значения переменной S (блок 3), повторяется N раз.
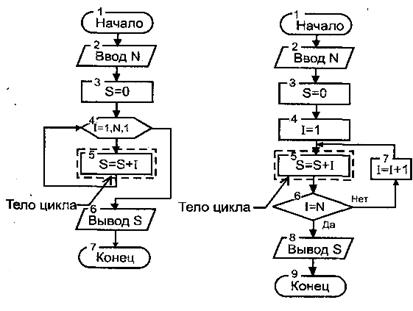
| Рис.3.1. Циклический алгоритм, использующий блок модификации. | Рис.3.2. Циклический алгоритм, использующий блок проверки условия |
Дата добавления: 2017-11-04; просмотров: 1102;
