Погрешность косвенного измерения
Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными.
Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку косвенных измерений.
Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.
Пусть физическая величина j(x, y, z, ...) является функцией ряда независимых аргументов x, y, z, ..., каждый из которых может быть определен экспериментально. Путем прямых измерений определяются величины 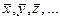 и оцениваются их средние абсолютные погрешности
и оцениваются их средние абсолютные погрешности  или средние квадратичные погрешности
или средние квадратичные погрешности 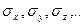 .
.
Средняя абсолютная погрешность косвенных измерений физической величины j вычисляется по формуле
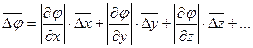
где 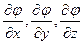 - частные производные от φ по x, y, z, вычисленные для средних значений соответствующих аргументов.
- частные производные от φ по x, y, z, вычисленные для средних значений соответствующих аргументов.
Так как в формуле использованы абсолютные величины всех членов суммы, то выражение для 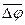 оценивает максимальную погрешность измерения функции при заданных максимальных ошибках независимых переменных.
оценивает максимальную погрешность измерения функции при заданных максимальных ошибках независимых переменных.
Средняя квадратичная погрешность косвенных измерений физической величины j

Относительная максимальная погрешность косвенных измерений физической величины j
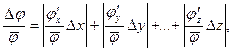
где 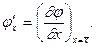 и т. д.
и т. д.
Аналогично можно записать относительную среднюю квадратичную погрешность косвенных измерений j
Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять относительную погрешность  . Для этого (в случае средней абсолютной погрешности) надо проделать следующее.
. Для этого (в случае средней абсолютной погрешности) надо проделать следующее.
1. Прологарифмировать выражение для косвенного измерения физической величины.
2. Продифференцировать его.
3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.
4. Взять выражение перед различными дифференциалами по модулю.
5. Формально заменить значки дифференциалов на значки абсолютной погрешности D.
Затем, зная e, можно вычислить абсолютную погрешность Dj по формуле
Dj = j×e
Пример 1.Вывод формулы для вычисления максимальной относительной погрешности косвенных измерений объёма цилиндра.
Выражение для косвенного измерения физической величины (исходная формула)
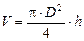
Величина диаметра D и высоты цилиндра h измеряются непосредственно приборами с погрешностями прямых измерений соответственноD D и Dh.
Прологарифмируем исходную формулу и получим
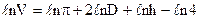
Продифференцируем полученное уравнение
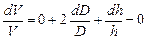
Заменив значки дифференциалов на значки абсолютной погрешности D, окончательно получим формулу для расчёта максимальной относительной погрешности косвенных измерений объёма цилиндра
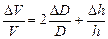
Дата добавления: 2017-10-09; просмотров: 3664;
