Действия над комплексными числами в алгебраической форме
Действия над комплексными числами в алгебраической форме.

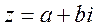 - алгебраическая форма записи комплексного числа,
- алгебраическая форма записи комплексного числа,
где а –действительная часть комплексного числа, b – мнимая часть комплексного числа, i – мнимая единица, 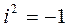
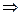
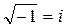 .
.
Действия над комплексными числами в алгебраической форме
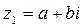 ,
, 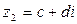 -данные комплексные числа
-данные комплексные числа
 1.Сложение: Чтобы найти сумму двух комплексных чисел , надо по отдельности сложить действительные и мнимые части, т.е.
1.Сложение: Чтобы найти сумму двух комплексных чисел , надо по отдельности сложить действительные и мнимые части, т.е.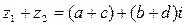
Пример 1: 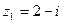 ,
, 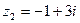 ,
, 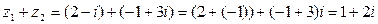
 2. Вычитание: Чтобы найти разность двух комплексных чисел , надо по отдельности вычесть действительные и мнимые части, т.е.
2. Вычитание: Чтобы найти разность двух комплексных чисел , надо по отдельности вычесть действительные и мнимые части, т.е.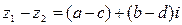
Пример 2: 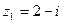 ,
, 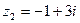 ,
, 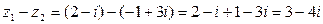
3.Умножение: Произведение комплексных чисел находится по распределительному закону умножения и определению мнимой единицы, т.е.раскрыть скобки, привести подобные, учитывая, что 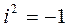
Пример 3: 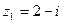 ,
, 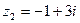 ,
, 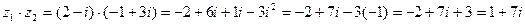
4. Деление:Числитель и знаменатель дроби умножить на выражение, сопряжённое знаменателю
Для комплексного числа 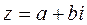 , сопряженным является число
, сопряженным является число 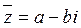
Для комплексного числа 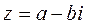 , сопряженным является число
, сопряженным является число 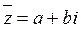
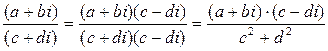
Пример 4: 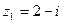 ,
, 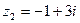
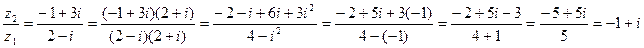
Тема № 2. Тригонометрическая форма комплексных чисел.
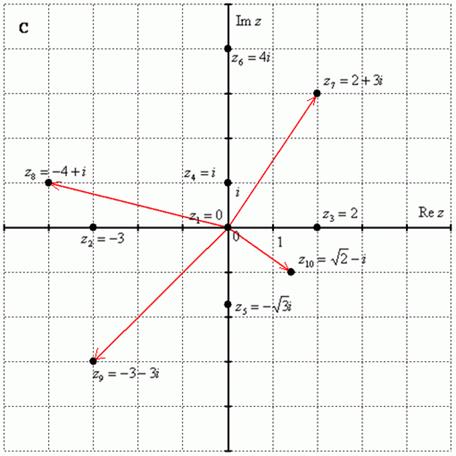
Каждое комплексное число a + bi геометрически изображается на плоскости как точка М(а;b) или как вектор ОМ. Ось Х является действительной осью, Ось Y является мнимой осью. Пример 1:
Пример 2: Аргументом ( [0, 2
Пример 3: Найдём аргумент комплексного числа
где r – модуль комплексного числа, Пример 4: Найти тригонометрическую форму записи комплексного числа
1) Найдём модуль: 2) Найдём аргумент: (-1;1) – координаты точки данного числа, 3) |
Тема № 3. Действия над комплексными числами в тригонометрической форме.
 1. Умножение. При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются
1. Умножение. При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются 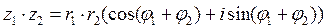
Пример1. Дано: 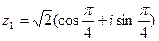 ,
, 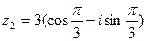 . Найти
. Найти 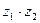
Решение: 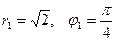 ,
, 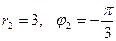 ,
, 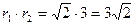 ,
, 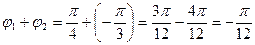 Ответ:
Ответ: 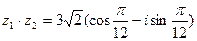
2. Деление. При делении двух комплексных чисел модуль первого из них делится на модуль второго, а из аргумента первого вычитается аргумент второго.

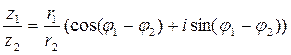
Пример 2. Дано: 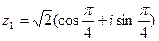 ,
, 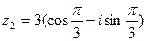 . Найти:
. Найти: 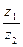
Регение: 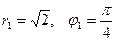 ,
, 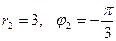 ,
, 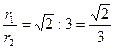 ,
, 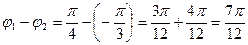 . Ответ:
. Ответ: 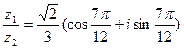
 3. Возведение в степень. При возведении комплексного числа z в степень n его модуль возводится в степень n, а аргумент умножается на n
3. Возведение в степень. При возведении комплексного числа z в степень n его модуль возводится в степень n, а аргумент умножается на n
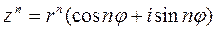
Пример 3.Дано: 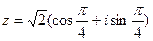 . Найти:
. Найти: 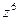 .
.
Решение: 
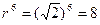 ,
, 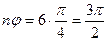 ,
, 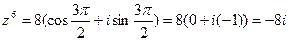
Ответ: 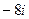
| <== предыдущая лекция | | | следующая лекция ==> |
| Основные правила работы архивов организаций 7 страница | | | Сущность и основные составляющие стратегического управления. |
Дата добавления: 2017-10-09; просмотров: 2044;

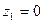
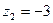
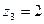
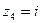
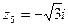
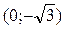
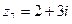
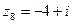
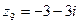
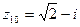
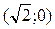
 Модулем ( r) комплексного числа называется длина вектора, соответствующего этому числу
Модулем ( r) комплексного числа называется длина вектора, соответствующего этому числу 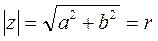
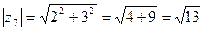 ,
, 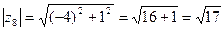 ,
, 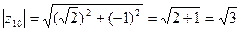
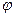 ) комплексного числа называется величина угла в радианах между положительным направлением действительной оси и вектором комплексного числа. Аргумент обозначается как ϕ = arg(z) и принадлежит полуинтервалу
) комплексного числа называется величина угла в радианах между положительным направлением действительной оси и вектором комплексного числа. Аргумент обозначается как ϕ = arg(z) и принадлежит полуинтервалу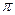 ).
).
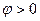 , если поворот против часовой стрелки,
, если поворот против часовой стрелки, 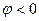 , если поворот по часовой стрелки.
, если поворот по часовой стрелки. 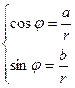 Аргумент комплексного числа можно найти через вспомогательный угол
Аргумент комплексного числа можно найти через вспомогательный угол 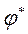 ,
, 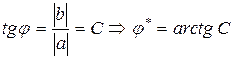 .
. 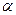 , рад
, рад
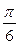
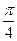
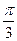
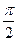
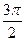
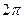
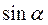
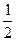
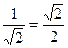
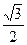
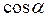
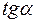
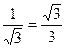
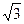
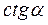
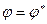
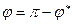
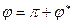
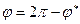
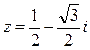 .
.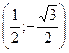 -координаты точки на плоскости данного числа,
-координаты точки на плоскости данного числа, 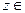 IV четверти.
IV четверти.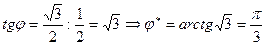 , так как число находится в IV четверти, то
, так как число находится в IV четверти, то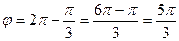 . Ответ:
. Ответ: 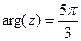

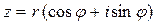 - тригонометрическая форма записи комплексного числа,
- тригонометрическая форма записи комплексного числа,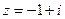 .
.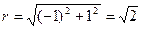 .
.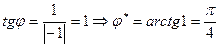 . Так как число находится во II четверти, то
. Так как число находится во II четверти, то 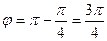
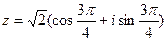 - тригонометрическая форма комплексного числа
- тригонометрическая форма комплексного числа