МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Основные этапы математического моделирования
Для обсуждения и обоснования основных подходов к разработке проблем математического моделирования технических устройств и процессов в них представляется целесообразным предварительно рассмотреть условную схему (рис. 1.1), определяющую последовательность проведения отдельных этапов общей процедуры вычислительного эксперимента. Исходной позицией этой схемы служит технический объект (ТО), под которым будем понимать конкретное техническое устройство, его агрегат или узел, систему устройств, процесс, явление или отдельную ситуацию в какой-либо системе или устройстве.
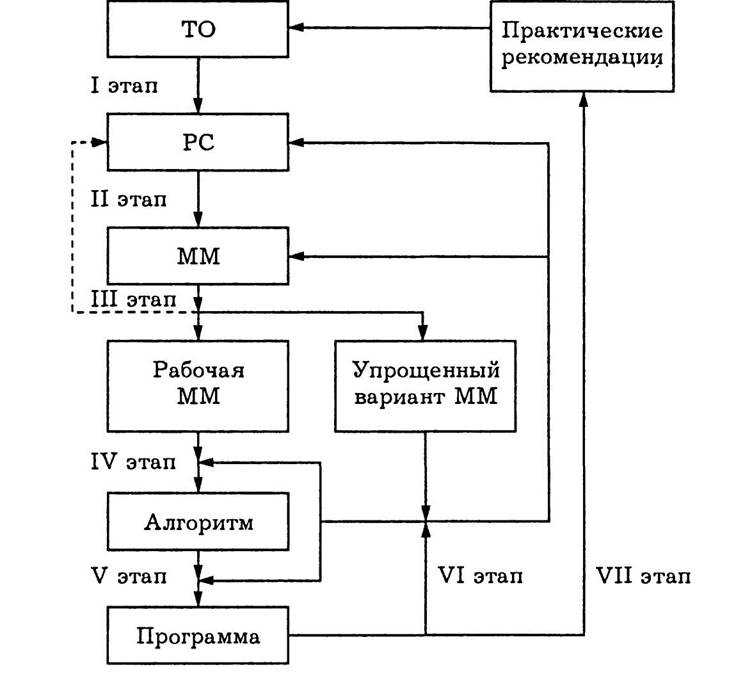
Рис. 1.1
На первом этапе осуществляют неформальный переход от рассматриваемого (разрабатываемого или существующего) ТО к его расчетной схеме (PC). При этом в зависимости от направленности вычислительного эксперимента и его конечной цели акцентируют те свойства, условия работы и особенности ТО, которые вместе с характеризующими их параметрами должны найти отражение в PC, и, наоборот, аргументируют допущения и упрощения, позволяющие не учитывать в PC те качества ТО, влияние которых предполагают в рассматриваемом случае несущественным. Иногда вместо PC используют термин содержательная модель* ТО, а в некоторых случаях — концептуальная модель. В сложившихся инженерных дисциплинах (например, в сопротивлении материалов, электротехнике и электронике) помимо описательной (вербальной) информации для характеристики PC разработаны специальные приемы и символы наглядного графического изображения. По ряду новых направлений развития техники подобная символика находится в стадии формирования.
При разработке новых ТО успешное проведение первого этапа в значительной мере зависит от профессионального уровня инженера, его творческого потенциала и интуиции. Полнота и правильность учета в PC свойств ТО, существенных с точки зрения поставленной цели исследования, являются основной предпосылкой получения в дальнейшем достоверных резульатов математического моделирования. И наоборот, сильная идеализация ТО ради получения простой PC может обесценить все последующие этапы исследования.
Содержание второго этапа состоит, по существу, в формальном, математическом описании PC. Это описание в виде математических соотношений, устанавливающих связь между параметрами, характеризующими PC TO, и называют математической моделью (ММ).
Надо сказать, что для некоторых типовых PC существуют банки ММ, что упрощает проведение второго этапа. Более того, одна и та же ММ может соответствовать PC из различных предметных областей. Однако при разработке новых ТО часто не удается ограничиться применением типовых PC и отвечающих им уже построенных ММ. Создание новых ММ или модификация существующих должны опираться на достаточно глубокую математическую подготовку и владение математикой как универсальным языком науки.
На третьем этапе проводят качественный и оценочный количественный анализ построенной ММ. При этом могут быть выявлены противоречия, ликвидация которых потребует уточнения или пересмотра PC (штриховая линия на рис. 1.1). Количественные оценки могут дать основания упростить модель, исключив из рассмотрения некоторые параметры, соотношения или их отдельные составляющие, несмотря на то что влияние описываемых ими факторов учтено в PC. В большинстве случаев, принимая дополнительные по отношению к PC допущения, полезно построить такой упрощенный вариант ММ, который позволял бы получить или привлечь известное точное решение. Это решение затем можно использовать для сравнения при тестировании результатов на последующих этапах. В некоторых случаях удается построить несколько ММ для одного и того же ТО, отличающихся различным уровнем упрощения. В этом случае говорят об иерархии ММ (греческое слово 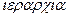 происходит от
происходит от 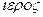 — священный и
— священный и 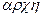 — власть и в данном случае означает упорядочение ММ по признаку их сложности и полноты).
— власть и в данном случае означает упорядочение ММ по признаку их сложности и полноты).
Построение иерархии ММ связано с различной детализацией свойств изучаемого ТО. Сравнение результатов исследования различных ММ может существенно расширить и обогатить знания об этом ТО. Кроме того, такое сравнение позволяет оценить достоверность результатов последующего вычислительного эксперимента: если более простая ММ правильно отражает некоторые свойства ТО, то результаты исследования этих свойств должны быть близки к результатам, полученным при использовании более полной и сложной ММ.
Итог анализа на рассматриваемом этапе — это обоснованный выбор рабочей ММ ТО, которая подлежит в дальнейшем детальному количественному анализу. Успех в проведении третьего этапа зависит, как правило, от глубины понимания связи отдельных составляющих ММ со свойствами ТО, нашедшими отражение в его PC, что предполагает органическое сочетание владения математикой и инженерными знаниями в конкретной предметной области.
Четвертый этап состоит в обоснованном выборе метода количественного анализа ММ, в разработке эффективного алгоритма вычислительного эксперимента, а пятый этап — в создании работоспособной программы, реализующей этот алгоритм средствами вычислительной техники. Для успешного проведения четвертого этапа необходимо владеть арсеналом современных методов вычислительной математики, а при математическом моделировании довольно сложных ТО выполнение пятого этапа требует профессиональной подготовки в области программирования на ЭВМ.
Получаемые на шестом этапе (в итоге работы программы) результаты вычислений должны прежде всего пройти тестирование путем сопоставления с данными количественного анализа упрощенного варианта ММ рассматриваемого ТО. Тестирование может выявить недочеты как в программе, так и в алгоритме и потребовать доработки программы или же модификации и алгоритма и программы. Анализ результатов вычислений и их инженерная интерпретация могут вызвать необходимость в корректировке PC и соответствующей ММ. После устранения всех выявленных недочетов триаду „модель — алгоритм — программа" можно использовать в качестве рабочего инструмента для проведения вычислительного эксперимента и выработки на основе получаемой количественной информации практических рекомендаций, направленных на совершенствование ТО, что составляет содержание седьмого, завершающего „технологический цикл" этапа математического моделирования.
Представленная последовательность этапов носит общий и универсальный характер, хотя в некоторых конкретных случаях она может и несколько видоизменяться. Если при разработке ТО можно использовать типовые PC и ММ, то отпадает необходимость в выполнении ряда этапов, а при наличии и соответствующего программного комплекса процесс вычислительного эксперимента становится в значительной степени автоматизированным. Однако математическое моделирование ТО, не имеющих близких прототипов, как правило, связано с проведением всех этапов описанного „технологического цикла".
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Из последовательности основных этапов математического моделирования (см. рис. 1.1) следует, что определяющую роль в нем играет математическая модель (ММ) изучаемого технического объекта. Поэтому прежде всего следует уделить внимание основным свойствам ММ и требованиям к ней, а также классификации ММ.
2.1. Понятие математической модели
Понятие математической модели (ММ), как и ряд других понятий, используемых в математическом моделировании, не имеет строгого формального определения. Тем не менее в это понятие вкладывают вполне конкретное содержание, с которым, в частности, тесно связано применение математики в инженерной практике. Более того, такие научные дисциплины, как механика, физика и их многочисленные разделы, являются, по существу, упорядоченными множествами ММ, построение которых сопровождается теоретическим обоснованием адекватного отражения этими моделями свойств рассматриваемых процессов и явлений. Именно посредством ММ научные дисциплины взаимодействуют с математикой.
Этапы развития многих естественно-научных направлений в познании законов природы и в совершенствовании техники — это построение последовательности все более точных и более полных ММ изучаемых процессов и явлений. Однако история науки знает не только случаи последовательного уточнения той или иной ММ, но и случаи отказа от некоторых ММ вследствие расхождений прогнозируемых ими результатов с реальностью.
Отвечающая реальности (адекватная) ММ является, как правило, большим научным достижением. Она позволяет провести детальное исследование изучаемого объекта и дать надежный прогноз его поведения в различных условиях. Но за адекватность ММ нередко приходится расплачиваться ее усложнением, что вызывает трудности при ее использовании. В этом случае на помощь математике и приходит современная вычислительная техника, существенно расширившая класс ММ, допускающих исчерпывающий количественный анализ.
Одни и те же ММ находят подчас совершенно различные приложения. Известно, например, что закон Ньютона притяжения двух материальных точек и закон взаимодействия двух точечных электрических зарядов при соответствующем выборе единиц измерения физических величин можно выразить одинаковыми формулами. При помощи одной и той же ММ, содержащей уравнение Пуассона
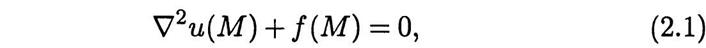
где 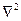 — дифференциальный оператор Лапласа, а
— дифференциальный оператор Лапласа, а 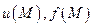 — искомая и заданная функции положения точки
— искомая и заданная функции положения точки 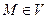 некоторой области V, можно изучать установившиеся процессы течения жидкости и распространения теплоты, распределение электрического потенциала, деформацию мембраны, механические напряжения при кручении бруса, фильтрацию нефти в нефтеносном слое или влаги в почве, распространение какой-либо примеси в воздухе или эпидемии в регионе. В каждой из перечисленных задач функции
некоторой области V, можно изучать установившиеся процессы течения жидкости и распространения теплоты, распределение электрического потенциала, деформацию мембраны, механические напряжения при кручении бруса, фильтрацию нефти в нефтеносном слое или влаги в почве, распространение какой-либо примеси в воздухе или эпидемии в регионе. В каждой из перечисленных задач функции 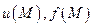 приобретают свой смысл, но их связь описывает общее для этих задач уравнение (2.1).
приобретают свой смысл, но их связь описывает общее для этих задач уравнение (2.1).
Приведенные примеры характеризуют свойство универсальности ММ. Благодаря этому свойству возникает „родство" между различными отраслями знаний, что ускоряет их совместное развитие. Такую общность и универсальность ММ можно объяснить тем, что в математике используют абстрактные основополагающие понятия, немногочисленные, но весьма емкие по содержанию. Это позволяет конкретные факты из самых различных областей знаний рассматривать как проявление этих понятий и отношений между ними. Совокупность таких понятий и отношений, выраженных при помощи системы математических символов и обозначений и отражающих некоторые свойства изучаемого объекта, и называют математической моделью этого объекта. В данном случае математика выступает, по существу, в роли универсального языка науки. Его универсальность французский математик Анри Пуанкаре (1854-1912) определил всего одной фразой: „Математика — это искусство называть разные вещи одним и тем же именем".
2.2. Структура математической модели
В достаточно общем случае изучаемый технический объект (ТО) количественно можно охарактеризовать векторами 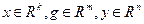 внешних, внутренних и выходных параметров соответственно. Одни и те же физические, механические или информационные характеристики ТО в моделях различного уровня и содержания могут выполнять роль как внешних или внутренних, так и выходных параметров.
внешних, внутренних и выходных параметров соответственно. Одни и те же физические, механические или информационные характеристики ТО в моделях различного уровня и содержания могут выполнять роль как внешних или внутренних, так и выходных параметров.
Например, для электронного усилителя выходными параметрами являются коэффициент усиления, полоса частот пропускаемых сигналов, входное сопротивление, рассеиваемая мощность, внешними — сопротивление и емкость нагрузки, напряжения источников питания, температура окружающей среды, а внутренними — сопротивления резисторов, емкости конденсаторов, характеристики транзисторов*2. Но если в качестве ТО рассматривать отдельно взятый транзистор, то такие его характеристики, как отпирающее напряжение и коллекторный ток, следует уже отнести к его выходным параметрам, а в качестве внешних надо будет рассматривать токи и напряжения, задаваемые коммутирующими с ним элементами усилителя.
При создании ТО значения выходных параметров или диапазоны их возможного изменения оговаривают в техническом задании на разработку ТО, тогда как внешние параметры характеризуют условия его функционирования.
В сравнительно простом случае математическая модель (ММ) ТО может представлять собой соотношение
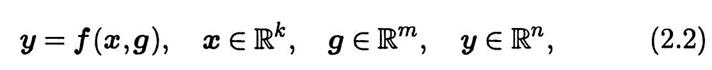
где 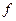 — векторная функция векторного аргумента. Модель в виде (2.2) позволяет легко вычислять выходные параметры по задаваемым значениям внешних и внутренних параметров, т.е. решать так называемую прямую задачу. В инженерной практике решение прямой задачи часто называют поверочным расчетом. При создании ТО возникает необходимость решать более сложную так называемую обратную задачу: по обусловленным техническим заданием на проектирование ТО значениям внешних и выходных параметров находить его внутренние параметры. В инженерной практике решению обратной задачи соответствует так называемый проектировочный расчет, часто имеющий целью оптимизацию внутренних параметров по некоторому критерию оптимальности. Однако при построении ММ ТО функция
— векторная функция векторного аргумента. Модель в виде (2.2) позволяет легко вычислять выходные параметры по задаваемым значениям внешних и внутренних параметров, т.е. решать так называемую прямую задачу. В инженерной практике решение прямой задачи часто называют поверочным расчетом. При создании ТО возникает необходимость решать более сложную так называемую обратную задачу: по обусловленным техническим заданием на проектирование ТО значениям внешних и выходных параметров находить его внутренние параметры. В инженерной практике решению обратной задачи соответствует так называемый проектировочный расчет, часто имеющий целью оптимизацию внутренних параметров по некоторому критерию оптимальности. Однако при построении ММ ТО функция 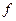 в (2.2) обычно заранее не известна и ее предстоит установить. Это наиболее сложная так называемая задача идентификации ММ (от латинского слова identifico — отождествляю, которому в данном случае придают смысл „распознаю").
в (2.2) обычно заранее не известна и ее предстоит установить. Это наиболее сложная так называемая задача идентификации ММ (от латинского слова identifico — отождествляю, которому в данном случае придают смысл „распознаю").
Задача идентификации может быть решена путем математической обработки информации о ряде таких состояний ТО, для каждого из которых известны (например, измерены экспериментально) значения выходных, внутренних и внешних параметров. Один из таких способов связан с применением регрессионного анализа [XVII]. Если информация о внутренних параметрах отсутствует или же внутреннее устройство ТО слишком сложно, то ММ такого ТО строят по принципу черного ящика — устанавливают соотношение между внешними и выходными параметрами путем исследования реакции ТО на внешние воздействия.
Теоретический путь построения ММ состоит в установлении связи между у, х и gв виде операторного уравнения
L(u(z))=0, (2.3)
где L — некоторый оператор (в общем случае нелинейный), О — нулевой элемент пространства, в котором действует этот оператор, z —вектор независимых переменных, в общем случае включающий время и пространственные координаты, а и — вектор фазовых переменных, включающий те параметры ТО, которые характеризуют его состояние. Но даже если возможно получить решение (2.3) и найти зависимость u(z) от z, то далеко не всегда удается представить ММ ТО в явном относительно вектора у виде (2.2). Поэтому именно (2.3) определяет в общем случае структуру ММ ТО, а (2.2) является более простым частным случаем такой модели.
2.3. Свойства математических моделей
Из сказанного ранее следует, что при изучении реально существующего или мыслимого технического объекта (ТО) математические методы применяют к его математической модели (ММ). Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям. Рассмотрим основные из этих свойств.
Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности ТО, которые интересуют нас с точки зрения поставленной цели проведения вычислительного эксперимента. Например, модель может достаточно полно описывать протекающие в объекте процессы, но не отражать его габаритные, массовые или стоимостные показатели. Так, ММ резистора в виде хорошо известной формулы U = IR закона Омаобладает свойством полноты лишь с точки зрения установления связи между падением электрического напряжения U на резисторе, его сопротивлением R и протекающим через него током силой I, но не дает никакой информации о размерах, массе, теплостойкости, стоимости и других характеристиках резистора, по отношению к которым она не является полной. Отметим попутно, что в рассматриваемой ММ сопротивление R резистора выступает в роли его внутреннего параметра, тогда как если задано U, то I будет выходным параметром, a U — внешним параметром, и наоборот.
Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров ТО, составляющих вектор
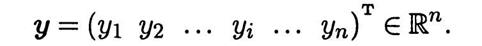
|
Пусть 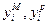 — найденное при помощи ММ и реальное значения i-го выходного параметра. Тогда относительная погрешность ММ по отношению к этому параметру будет равна
— найденное при помощи ММ и реальное значения i-го выходного параметра. Тогда относительная погрешность ММ по отношению к этому параметру будет равна
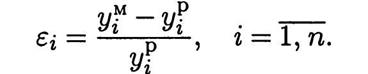
В качестве скалярной оценки вектора
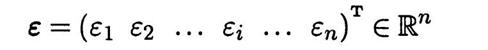
можно принять какую-либо его норму, например
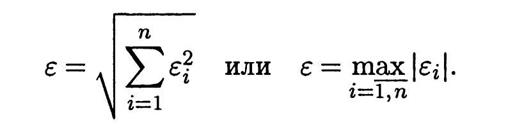
Поскольку выходные параметры ТО при помощи ММ связаны с его внешними и внутренними параметрами, т. е, как количественная характеристика точности модели этого ТО, будет зависеть от координат векторов х и y.
Адекватность ММ— это способность ММ описывать выходные параметры ТО с относительной погрешностью не более некоторого заданного значения 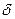 . Пусть при некоторых ожидаемых номинальных значениях внешних параметров ТО, составляющих вектор хном, из условия минимума
. Пусть при некоторых ожидаемых номинальных значениях внешних параметров ТО, составляющих вектор хном, из условия минимума 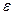 путей решения задачи конечномерной оптимизации [XIV] найдены значения внутренних параметров, составляющие вектор gном иобеспечивающие минимальное значение emin относительной погрешности ММ. Тогда при фиксированном векторе δ можно построить множество
путей решения задачи конечномерной оптимизации [XIV] найдены значения внутренних параметров, составляющие вектор gном иобеспечивающие минимальное значение emin относительной погрешности ММ. Тогда при фиксированном векторе δ можно построить множество
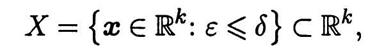
называемое областью адекватности данной ММ. Ясно, что 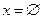 при
при 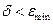 , а чем больше заданное значение
, а чем больше заданное значение 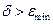 , тем шире область адекватности ММ, т.е. эта ММ применима в более широком диапазоне возможного изменения внешних параметров ТО.
, тем шире область адекватности ММ, т.е. эта ММ применима в более широком диапазоне возможного изменения внешних параметров ТО.
В более общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик ТО, которые важны в данном конкретном случае. Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик того же ТО. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом качественный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ естественно понимать лишь правильное качественное описание поведения изучаемых объектов или их систем. Экономичность ММ оценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Очевидно, что требования экономичности, высокой точности и достаточно широкой области адекватности ММ противоречивы и на практике могут быть удовлетворены лишь на основе разумного компромисса. Свойство экономичности ММ часто связывают с ее простотой. Более того, количественный анализ некоторых упрощенных вариантов ММ может быть осуществлен и без привлечения современной вычислительной техники. Однако его результаты могут иметь лишь ограниченную ценность на стадии отладки алгоритма или ЭВМ-программы (см. 1.2 и рис. 1.1), если упрощение ММ не согласовано с расчетной схемой ТО.
Робастность ММ (от английского слова robust — крепкий, устойчивый) характеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину, а также использование в ММ функций, быстро изменяющихся в промежутке, где значение аргумента известно с невысокой точностью. Иногда стремление увеличить полноту ММ приводит к снижению ее робастности вследствие введения дополнительных параметров, известных с невысокой точностью или входящих в слишком приближенные соотношения.
Продуктивность ММ связана с возможностью располагать достаточно достоверными исходными данными. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретного ТО теряет смысл. Ее можно будет использовать лишь для оценки характеристик некоторого класса ТО с гипотетическими исходными данными.
Наглядность ММ является ее желательным, но необязательным свойством. Тем не менее использование ММ и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это обычно позволяет ориентировочно предвидеть результаты вычислительного эксперимента и облегчает контроль их правильности.
В дальнейшем на конкретных примерах будут проиллюстрированы отмеченные выше свойства ММ (см. 3 и 6).
2.4. Структурные и функциональные
модели
Различные особенности и признаки математических моделей (ММ) лежат в основе их типизации (или классификации). Среди таких признаков выделяют характер отображаемых свойств технического объекта (ТО), степень их детализации, способы получения и представления ММ.
Один из существенных признаков классификации связан с отражением в ММ тех или иных особенностей ТО. Если ММ отображает устройство ТО и связи между составляющими его элементами, то ее называют структурной математической моделью. Если же ММ отражает происходящие в ТО физические, механические, химические или информационные процессы, то ее относят к функциональным математическим моделям. Ясно, что могут существовать и комбинированные ММ, которые описывают как функционирование, так и устройство ТО. Такие ММ естественно называть структурно-функциональными математическими моделями.
Структурные ММ делят на топологические и геометрические составляющие два уровня иерархии ММ этого типа. Первые отображают состав ТО и связи между его элементами. Топологическую ММ целесообразно применять на начальной стадии исследования сложного по структуре ТО, состоящего из большого числа элементов, прежде всего для уяснения и уточнения их взаимосвязи. Такая ММ имеет форму графов, таблиц, матриц, списков и т.п., и ее построению обычно предшествует разработка структурной схемы ТО.
Геометрическая ММ дополнительно к информации, представленной в топологической ММ, содержит сведения о форме и размерах ТО и его элементах, об их взаимном расположении. В геометрическую ММ обычно входят совокупность уравнений линий и поверхностей и алгебрологические соотношения, определяющие принадлежность областей пространства телу ТО или его элементам. Такую ММ иногда задают координатами некоторого множества точек, по которым интерполированием можно построить ограничивающие область линии или поверхности. Границы области задают и кинематическим способом: линию — как траекторию движения точки, а поверхность — как результат перемещения линии. Возможно представление формы и размеров области совокупностью типовых фрагментов достаточно простой конфигурации. Такой способ характерен, например, для метода конечных элементов [XIII], широко используемого в математическом моделировании.
Геометрические ММ находят применение при проектировании ТО, разработке технической документации и технологических процессов изготовления деталей (например, на станках с числовым программным управлением).
Функциональные ММ состоят из соотношений, связывающих между собой фазовые переменные, т.е. внутренние, внешние и выходные параметры ТО. Функционирование сложных ТО нередко удается описать лишь при помощи совокупности его реакций на некоторые известные (или заданные) входные воздействия (сигналы). Такую разновидность функциональной ММ относят к типу черного ящика и обычно называют имитационной математической моделью, имея в виду, что она лишь имитирует внешние проявления функционирования ТО, не раскрывая и не описывая существа протекающих в нем процессов. Имитационные ММ находят широкое применение в технической кибернетике— научном направлении, изучающем системы управления сложными ТО.
По форме представления имитационная ММ является примером алгоритмической математической модели, поскольку связь в ней между внешними и выходными параметрами ТО удается описать лишь в форме алгоритма, пригодного для реализации в виде ЭВМ-программы. По этому признаку к типу алгоритмических относят более широкий класс как функциональных, так и структурных ММ. Если связи между параметрами ТО можно выразить в аналитической форме, то говорят об аналитических математических моделях. При построении иерархии ММ одного и того же ТО обычно стремятся к тому, чтобы упрощенный вариант ММ (см. 1.2) был представлен в аналитической форме, допускающей точное решение, которое можно было бы использовать для сравнения при тестировании результатов, полученных при помощи более полных и поэтому более сложных вариантов ММ.
Ясно, что ММ конкретного ТО по форме представления может включать признаки как аналитической, так и алгоритмической ММ. Более того, на стадии количественного исследования достаточно сложной аналитической ММ и проведения вычислительного эксперимента на ее основе разрабатывают алгоритм, который реализуют в виде ЭВМ-программы, т.е. в процессе математического моделирования аналитическую ММ преобразуют в алгоритмическую ММ.
2.5. Теоретические и эмпирические
модели
По способу получения математические модели (ММ) делят на теоретические и эмпирические. Первые получают в результате изучения свойств технического объекта (ТО) и протекающих в нем процессов, а вторые являются итогом обработки результатов наблюдения внешних проявлений этих свойств и процессов. Один из способов построения эмпирических ММ заключается в проведении экспериментальных исследований, связанных с измерением фазовых переменных ТО, и в последующем обобщении результатов этих измерений в алгоритмической форме или в виде аналитических зависимостей. Поэтому эмпирическая ММ по форме представления может содержать признаки как алгоритмической, так и аналитической математической модели. Таким образом, построение эмпирической ММ сводится к решению задачи идентификации.
При построении теоретических ММ прежде всего стремятся использовать известные фундаментальные законы сохранения таких субстанций, как масса, электрический заряд, энергия, количество движения и момент количества движения. Кроме того, привлекают определяющие соотношения (называемые также уравнениями состояния), в роли которых могут выступать так называемые феноменологические законы (например, уравнение Клапейрона — Менделеева состояния совершенного газа, закон Ома о связи силы тока в проводнике и падения электрического напряжения, закон Гука о связи деформации и механического напряжения в линейно упругом материале, закон Фурье [XII] о связи градиента температуры в теле с плотностью теплового потока и т.п.).
Сочетание теоретических соображений качественного характера с обработкой результатов наблюдения внешних проявлений свойств изучаемого ТО приводит к смешанному типу ММ, называемых полуэмпирическими. При построении таких ММ используют основные положения теории размерностей, в том числе так называемую П-теорему (Пи-теорему*): если между п параметрами, характеризующими изучаемый объект, существует зависимость, имеющая физический смысл, то эту зависимость можно представить в виде зависимости между 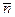 = п — к их безразмерными комбинациями, где к — число независимых единиц измерения, через которые можно выразить размерности этих параметров. При этом п определяет число независимых (не выражаемых друг через друга) безразмерных комбинаций, обычно называемых критериями подобия .
= п — к их безразмерными комбинациями, где к — число независимых единиц измерения, через которые можно выразить размерности этих параметров. При этом п определяет число независимых (не выражаемых друг через друга) безразмерных комбинаций, обычно называемых критериями подобия .
Объекты, для которых равны значения соответствующих критериев подобия, считают подобными. Например, любой треугольник однозначно определен длинами a, b и с его сторон, т.е n= 3, a k = 1. Поэтому, согласно 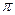 -теореме, множество подобных треугольников можно задать значениями
-теореме, множество подобных треугольников можно задать значениями 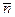 = п — к = 2 критериев подобия. В качестве таких критериев можно выбрать безразмерные отношения длин сторон: b/а и с/а или любые два других независимых отношения. Так как углы треугольника однозначно связаны с отношениями сторон и являются безразмерными величинами, то множество подобных треугольников можно определить равенством двух соответствующих углов или равенством угла и отношения длин прилегающих к нему сторон. Все перечисленные варианты соответствуют известным признакам подобия треугольников.
= п — к = 2 критериев подобия. В качестве таких критериев можно выбрать безразмерные отношения длин сторон: b/а и с/а или любые два других независимых отношения. Так как углы треугольника однозначно связаны с отношениями сторон и являются безразмерными величинами, то множество подобных треугольников можно определить равенством двух соответствующих углов или равенством угла и отношения длин прилегающих к нему сторон. Все перечисленные варианты соответствуют известным признакам подобия треугольников.
Для успешного применения П-теоремы к построению моделей ТО необходимо располагать полным набором параметров, описывающих изучаемый объект, причем выбор этих параметров должен опираться на аргументированный качественный анализ тех свойств и особенностей ТО, влияние которых существенно в данном конкретном случае. Отметим, что такой анализ необходим при любом способе построения ММ, и проиллюстрируем это положение примерами.
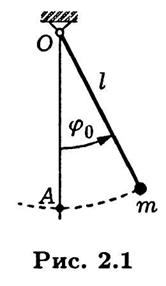
Пример 2.1.Рассмотрим хорошо известную расчетную схему математического маятника (рис. 2.1) в виде материальной точки массой 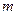 , подвешенной на невесомом стержне постоянной длины
, подвешенной на невесомом стержне постоянной длины 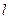 , который может свободно вращаться относительно горизонтальной оси, проходящей через точку О. Отклонение маятника на угол
, который может свободно вращаться относительно горизонтальной оси, проходящей через точку О. Отклонение маятника на угол 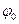 от его вертикального положения
от его вертикального положения
|
равновесия приведет к возрастанию потенциальной энергии материальной точки на величину 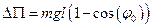 где
где 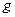 — ускорение свободного падения. Если после отклонения маятник начнет движение, то при отсутствии сопротивления он в силу закона сохранения энергии будет совершать незатухающие колебания относительно положения равновесия (точка А на рис. 2.1). При прохождении положения равновесия скорость v материальной точки является наибольшей по абсолютной величине, поскольку в этом положении кинетическая энергия этой точки равна
— ускорение свободного падения. Если после отклонения маятник начнет движение, то при отсутствии сопротивления он в силу закона сохранения энергии будет совершать незатухающие колебания относительно положения равновесия (точка А на рис. 2.1). При прохождении положения равновесия скорость v материальной точки является наибольшей по абсолютной величине, поскольку в этом положении кинетическая энергия этой точки равна 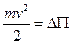 , так
, так
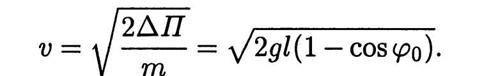
Пусть необходимо установить зависимость периода Т колебаний маятника (т.е. наименьшего промежутка времени, через который маятник возвращается в некоторое фиксированное положение, не совпадающее с положением равновесия) от параметров 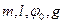 (параметр v следует исключить из рассмотрения, поскольку его удалось выразить через указанные выше параметры). Размерности [.] четырех указанных параметров и периода Т колебаний можно выразить через к = 3 независимые стандартные единицы измерения: [Т] = с, [т] = кг, [l] = мс, [
(параметр v следует исключить из рассмотрения, поскольку его удалось выразить через указанные выше параметры). Размерности [.] четырех указанных параметров и периода Т колебаний можно выразить через к = 3 независимые стандартные единицы измерения: [Т] = с, [т] = кг, [l] = мс, [ 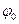 ] = 0 и [g] = м/с2. Поэтому в силу П-теоремы из п = 5 параметров можно составить
] = 0 и [g] = м/с2. Поэтому в силу П-теоремы из п = 5 параметров можно составить 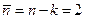 безразмерные комбинации, причем угол
безразмерные комбинации, причем угол 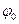 , будучи безразмерным, является одной из них. Во вторую безразмерную комбинацию не удается включить массу m материальной точки, поскольку единица измерения массы (кг) входит лишь в размерность массы. Следовательно, величина m не является аргументом искомой зависимости, что можно установить и при построении теоретической ММ рассматриваемого маятника (см. пример 5.12). После исключения параметра m имеем п = 4 и к = 2, т.е. снова п = 2, так что наряду с безразмерным параметром
, будучи безразмерным, является одной из них. Во вторую безразмерную комбинацию не удается включить массу m материальной точки, поскольку единица измерения массы (кг) входит лишь в размерность массы. Следовательно, величина m не является аргументом искомой зависимости, что можно установить и при построении теоретической ММ рассматриваемого маятника (см. пример 5.12). После исключения параметра m имеем п = 4 и к = 2, т.е. снова п = 2, так что наряду с безразмерным параметром 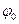 остальные
остальные
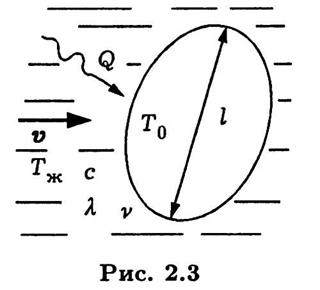
Пример 2.3.Пусть поток несжимаемой жидкости обтекает неподвижное твердое тело заданной формы, имеющее характерный размер 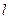 и постоянную температуру То (рис. 2.3). Скорость v и температура Тж > То жидкости на большом (по сравнению с I) расстоянии от тела сохраняют постоянные значения. Необходимо при некотором фиксированном положении тела относительно направления вектора v скорости найти количество теплоты Q, передаваемое в единицу времени от жидкости к телу и называемое тепловым потоком.
и постоянную температуру То (рис. 2.3). Скорость v и температура Тж > То жидкости на большом (по сравнению с I) расстоянии от тела сохраняют постоянные значения. Необходимо при некотором фиксированном положении тела относительно направления вектора v скорости найти количество теплоты Q, передаваемое в единицу времени от жидкости к телу и называемое тепловым потоком.
|
Процесс передачи теплоты локализован у поверхности тела и зависит не только от перечисленных параметров, но и от объемной теплоемкости с и коэффициента теплопроводности 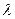 жидкости, поскольку эти параметры характеризуют способность жидкости подводить тепловую энергию и передавать ее поверхности тела. Подвод тепловой энергии к телу также зависит от распределения скорости жидкости у его поверхности. В случае идеальной (невязкой) жидкости оно однозначно определено фиксированным положением тела относительно вектора v, а для вязкой жидкости зависит и от соотношения между силами вязкости и инерции, характеризуемого коэффициентом вязкости
жидкости, поскольку эти параметры характеризуют способность жидкости подводить тепловую энергию и передавать ее поверхности тела. Подвод тепловой энергии к телу также зависит от распределения скорости жидкости у его поверхности. В случае идеальной (невязкой) жидкости оно однозначно определено фиксированным положением тела относительно вектора v, а для вязкой жидкости зависит и от соотношения между силами вязкости и инерции, характеризуемого коэффициентом вязкости 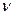 , называемым кинематическим и измеряемым в м2/с.
, называемым кинематическим и измеряемым в м2/с.
При сравнительно близких значениях Тж и То естественно предположить, что тепловой поток зависит не от каждой из этих температур, а от их разности 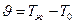 . Тогда в случае идеальной жидкости имеем п = 6 размерных параметров, размерности которых можно выразить через к = 4 независимые стандартные единицы измерения: [l] = м, [v] = м/с,
. Тогда в случае идеальной жидкости имеем п = 6 размерных параметров, размерности которых можно выразить через к = 4 независимые стандартные единицы измерения: [l] = м, [v] = м/с,
[ 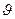 ] =K, [Q]=Дж/с=Вт=н
] =K, [Q]=Дж/с=Вт=н  м/с, [c]=Дж/(м3К)=кг/(м
м/с, [c]=Дж/(м3К)=кг/(м  с2
с2  К), [
К), [ 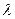 ]=Вт/(м
]=Вт/(м  К)=кг
К)=кг  м/(с3К), где Дж (джоуль) и Вт (ватт) — единицы измерения энергии (работы) и мощности соответственно, а К (кельвин ) — единица измерения температуры в абсолютной шкале. В силу П-теоремы из этих параметров можно составить лишь п = п — к = 2 независимые безразмерные комбинации, например
м/(с3К), где Дж (джоуль) и Вт (ватт) — единицы измерения энергии (работы) и мощности соответственно, а К (кельвин ) — единица измерения температуры в абсолютной шкале. В силу П-теоремы из этих параметров можно составить лишь п = п — к = 2 независимые безразмерные комбинации, например 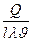 и
и 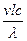 . В итоге приходим к функциональной зависимости
. В итоге приходим к функциональной зависимости

установленной в 1915 г. Дж.У. Стреттом .
Отношение q = Q/S называют усредненной по площади S поверхности тела плотностью теплового потока и измеряют в Вт/м2. Так как для геометрически подобных тел 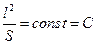 , то (2.7) можно представить в виде
, то (2.7) можно представить в виде
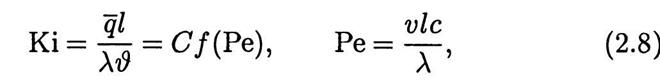
где Ki — тепловой критерий Кирпичева и Ре — критерий Пекле. Интенсивность теплообмена на поверхности тела обычно характеризуют усредненным коэффициентом теплоотдачи 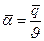 — , измеряемым в Вт/(м2К). Тогда вместо (2.8) получим
— , измеряемым в Вт/(м2К). Тогда вместо (2.8) получим
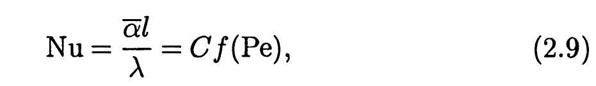
где Nu — критерий (число) Нуссельта . Вид функции 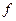 в (2.7)-(2.9) нельзя установить в рамках теории размерностей и его приходится определять путем обработки результатов экспериментов, хотя в некоторых простых случаях удается построить и теоретические ММ процесса теплообмена.
в (2.7)-(2.9) нельзя установить в рамках теории размерностей и его приходится определять путем обработки результатов экспериментов, хотя в некоторых простых случаях удается построить и теоретические ММ процесса теплообмена.
В случае вязкой жидкости имеем п = 7 размерных параметров, размерности которых по-прежнему можно выразить через к = 4 независимые единицы измерения, т.е. число независмых безразмерных комбинаций равно 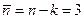 . К рассмотренным выше следует добавить любую безразмерную комбинацию, включающую новый параметр и. Эту комбинацию можно выбрать, например, в виде
. К рассмотренным выше следует добавить любую безразмерную комбинацию, включающую новый параметр и. Эту комбинацию можно выбрать, например, в виде 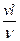 или
или 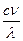 . В первом случае ее называют критерием (числом) Рейнолъдса и обозначают Re =
. В первом случае ее называют критерием (числом) Рейнолъдса и обозначают Re = 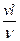 , а во втором — критерием (числом)Прандтля и обозначают Рг =
, а во втором — критерием (числом)Прандтля и обозначают Рг = 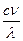 . Критерий Прандтля характеризует только свойства жидкости, а критерий Рейнольдса — соотношение между инерционными силами и силами вязкого трения. В итоге вместо (2.9) получим
. Критерий Прандтля характеризует только свойства жидкости, а критерий Рейнольдса — соотношение между инерционными силами и силами вязкого трения. В итоге вместо (2.9) получим
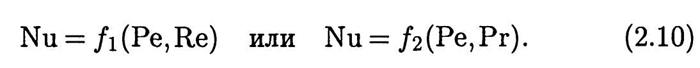
Так как Ре = RePr, то в случае вязкой жидкости критерий Нуссельта может быть представлен функцией любых двух из трех аргументов Ре, Re, Pr.
Ясно, что при наличии трех и более безразмерных комбинаций параметров построение полуэмпирической ММ существенно усложняется. В этом случае обычно выделяют так называемый определяемый критерий (в примере 2.3 это Ki или Nu), a остальные критерии относят к определяющим и проводят несколько серий экспериментальных измерений для установления функциональной зависимости определяемого критерия от двух или более определяющих, рассматриваемых в качестве аргументов искомой функции (в (2.10) это функции 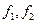 ). В каждой серии измерений размерные параметры изменяют таким образом, чтобы изменялось значение лишь одного из определяющих критериев. Тогда обработка результатов такой серии измерений позволяет выявить функциональную зависимость определяемого критерия от одного из аргументов при фиксированных значениях остальных. В итоге в некоторой области изменения значений определяющих критериев удается с некоторой степенью приближения построить искомую функцию, т.е. решить задачу идентификации полуэмпирической ММ.
). В каждой серии измерений размерные параметры изменяют таким образом, чтобы изменялось значение лишь одного из определяющих критериев. Тогда обработка результатов такой серии измерений позволяет выявить функциональную зависимость определяемого критерия от одного из аргументов при фиксированных значениях остальных. В итоге в некоторой области изменения значений определяющих критериев удается с некоторой степенью приближения построить искомую функцию, т.е. решить задачу идентификации полуэмпирической ММ.
Отметим, что применение 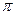 -теоремы к аналитической ММ, представленной в виде уравнений, позволяет привести их к безразмерной форме и сократить число параметров, характеризующих изучаемый ТО. Это упрощает качественный анализ и позволяет еще до проведения количественного анализа оценить влияние отдельных факторов (см. Д.2.2). Кроме того, безразмерная форма ММ дает возможность представить в более компактном виде результаты ее количественного анализа.
-теоремы к аналитической ММ, представленной в виде уравнений, позволяет привести их к безразмерной форме и сократить число параметров, характеризующих изучаемый ТО. Это упрощает качественный анализ и позволяет еще до проведения количественного анализа оценить влияние отдельных факторов (см. Д.2.2). Кроме того, безразмерная форма ММ дает возможность представить в более компактном виде результаты ее количественного анализа.
2.6. Особенности функциональных моделей
Одной из характерных особенностей функциональной математической модели (ММ) является наличие или отсутствие среди ее параметров случайных величин. При наличии таких величин ММ называют стохастической, а при их отсутствии — детерминированной.
Далеко не все параметры реальных технических объектов (ТО) можно характеризовать вполне определенными значениями. Поэтому ММ таких ТО, строго говоря, следует отнести к стохастическим. Например, если изучаемый ТО является изделием массового производства и его внутренние параметры могут принимать случайные значения в пределах допусков, установленных относительно номинальных значений, то и выходные параметры ТО будут случайными величинами. Случайными могут быть и значения внешних параметров при воздействии на ТО таких факторов, как порывы ветра, турбулентные пульсации, сигналы на фоне шума и т.п.
Для анализа стохастических ММ необходимо использовать методы теории вероятностей, случайных процессов и математической статистики. Однако основная трудность их применения обычно связана с тем, что вероятностные характеристики случайных величин (математические ожидания, дисперсии, законы распределения) часто не известны или известны с невысокой точностью, т.е. ММ не удовлетворяет требованию продуктивности ММ. В таких случаях эффективнее использовать ММ, более грубую по сравнению со стохастической, но и более устойчивую по отношению к недостоверности исходных данных, т.е. в большей мере удовлетворяющую требованию робастности.
Существенным признаком классификации ММ является их возможность описывать изменение параметров ТО во времени. Рассмотренная в примере 2.4 ММ теплообмена тела с окружающей средой учитывает такое изменение, и ее относят к нестационарным (или эволюционным) математическим моделям. Если при этом в ММ отражено влияние инерционных свойств ТО, то ее обычно называют динамической. В противоположность этому ММ, которая не учитывает изменение во времени параметров ТО, называют статической. Рассмотренные в примерах 2.2 и 2.3 ММ являются статическими. Несмотря на движение воздушного потока и жидкости, обтекающих профиль крыла и нагреваемое тело соответственно, все параметры, характеризующие эти процессы остаются постоянными во времени.
Если изменение параметров ТО происходит столь медленно, что в рассматриваемый фиксированный момент времени этим изменением можно пренебречь, то говорят о квазистатической математической модели. Например, в медленно протекающих механических процессах можно пренебречь инерционными силами, при малой скорости изменения температуры — тепловой инерцией тела, а при медленно изменяющейся силе тока в электрической цепи — индуктивностью элементов этой цепи. Стационарные математические модели описывают ТО, в которых протекают так называемые установившиеся процессы, т.е. процессы, в которых интересующие нас выходные параметры постоянны во времени. К установившимся относят и периодические процессы, в которых некоторые выходные параметры остаются неизменными, а остальные претерпевают колебания. Например, ММ математического маятника (см. пример 2.1) является стационарной по отношению к не зависящим от времени периоду и полуразмаху колебаний, хотя материальная точка перемещается во времени относительно положения равновесия.
Если интересующие нас выходные параметры ТО изменяются медленно и в рассматриваемый фиксированный момент времени таким изменением можно пренебречь, то говорят о квазистационарной математической модели. При описании некоторых процессов нестационарная ММ может быть преобразована в квазистационарную соответствующим выбором системы координат. Например, при дуговой электросварке температурное поле в свариваемых стальных листах в окрестности движущегося с постоянной скоростью электрода в неподвижной системе координат описывает нестационарная ММ, а в подвижной системе координат, связанной с электродом, — квазистационарная ММ.
Важным с точки зрения последующего анализа свойством ММ является ее линейность. В линейной математической модели ТО его параметры связаны линейными соотношениями. Это означает, что при изменении какого-либо внешнего (или внутреннего) параметра ТО линейная ММ предсказывает линейное изменение зависящего от него выходного параметра, а при изменении двух или более параметров — сложение их влияний, т.е. такая ММ обладает свойством суперпозиции (от латинского слова superpositio — наложение). Если ММ не обладает свойством суперпозиции, то ее называют нелинейной.
Для количественного анализа линейных ММ разработано большое число математических методов, тогда как возможности анализа нелинейных ММ связаны в основном с методами вычислительной математики. Чтобы для исследования нелинейной ММ ТО можно было использовать аналитические методы, ее обычно линеаризуют, т.е. нелинейные соотношения между параметрами заменяют приближенными линейными и получают так называемую линеаризованную математическую модель рассматриваемого ТО. Так как линеаризация связана с внесением дополнительных погрешностей, то к результатам анализа линеаризованной модели следует относиться с определенной осторожностью. Дело в том, что линеаризация ММ может привести к утрате или существенному искажению реальных свойств ТО. Учет в ММ нелинейных эффектов особенно важен, например, при описании смены форм движения или положений равновесия ТО, когда малые изменения внешних параметров могут вызвать качественные изменения в его состоянии.
Каждый параметр ТО может быть двух типов — непрерывно изменяющимся в некотором промежутке своих значений или принимающим только некоторые дискретные значения. Возможна и промежуточная ситуация, когда в одной области параметр принимает все возможные значения, а в другой — только дискретные. В связи с этим выделяют непрерывные, дискретные и смешанные математические модели. В процессе анализа ММ этих типов могут быть преобразованы одна в другую, но при таком преобразовании следует контролировать выполнение требования адекватности ММ рассматриваемому ТО.
2.7. Иерархия математических моделей и формы их представления
При математическом моделировании достаточно сложного технического объекта (ТО) описать его поведение одной математической моделью (ММ), как правило, не удается, а если такая ММ и была бы построена, то она оказалась бы слишком сложной для количественного анализа. Поэтому к таким ТО обычно применяют принцип декомпозиции. Он состоит в условном разбиении ТО на отдельные более простые блоки и элементы, допускающие их независимое исследование с последующим учетом взаимного влияния блоков и элементов друг на друга. В свою очередь, принцип декомпозиции можно применить и к каждому выделенному блоку вплоть до уровня достаточно простых элементов. В таком случае возникает иерархия ММ связанных между собой блоков и элементов.
Иерархические уровни выделяют и для отдельных типов ММ. Например, среди структурных математических моделей ТО к более высокому уровню иерархии относят топологические математические модели, а к более низкому уровню, характеризующемуся большей детализацией ТО, — геометрические математические модели.
Среди функциональных математических моделей иерархические уровни отражают степень детализации описания процессов, протекающих в ТО, его блоках или элементах. С этой точки зрения обычно выделяют три основных уровня: микро-, макро- и метауровень.
Математические модели микроуровня описывают процессы в системах с распределенными параметрами (в континуальных системах), а математические модели макроуровня — в системах с сосредоточенными параметрами (в дискретных системах). В первых из них фазовые переменные могут зависеть как от времени, так и от пространственных координат, а во вторых — только от времени.
Если в ММ макроуровня число фазовых переменных имеет порядок 104-105, то количественный анализ такой ММ становится громоздким и требует значительных затрат вычислительных ресурсов. Кроме того, при столь большом числе фазовых переменных трудно выделить существенные характеристики ТО и особенности его поведения. В таком случае путем объединения и укрупнения элементов сложного ТО стремятся уменьшить число фазовых переменных за счет исключения из рассмотрения внутренних параметров элементов, ограничиваясь лишь описанием взаимных связей между укрупненными элементами. Такой подход характерен для математических моделей метауровня.
ММ метауровня обычно относят к высшему уровню иерархии, ММ макроуровня — к среднему, а ММ микроуровня — к низшему. Наиболее распространенной формой представления динамической (эволюционной) математической модели микроуровня является формулировка краевой задачи для дифференциальных уравнений математической физики [XII]. Такая формулировка включает дифференциальные уравнения с частными производными и краевые условия. В свою очередь, краевые условия содержат начальные условия — распределения искомых фазовых переменных в некоторый момент времени, принимаемый за начальный, в пространственной области, конфигурация которой соответствует рассматриваемому ТО или его элементу, — и граничные условия на границах этой области. При представлении ММ целесообразно использовать безразмерные переменные (независимые и искомые) и коэффициенты уравнений, сократив число параметров, характеризующих рассматриваемый ТО (см. Д.2.2).
ММ микроуровня называют одномерной, двумерной или трехмерной, если искомые фазовые переменные зависят от одной, двух или трех пространственных координат соответственно. Два последних типа ММ объединяют в многомерные математические модели микроуровнл. Одномерная ММ микроуровня, фазовые переменные в которой не зависят от времени, имеет представление в виде системы ОДУ с заданными граничными условиями (в простейшем случае одного фазового переменного такая ММ включает лишь одно ОДУ и граничные условия).
Поскольку краевой задаче, содержащей дифференциальные уравнения с частными производными и краевые условия, можно поставить в соответствие интегральную формулировку , то и ММ микроуровня также может быть представлена в интегральной форме. При определенных условиях интегральную форму краевой задачи удается привести к вариационной формулировке в виде функционала , который допустимо рассматривать на некотором множестве функций, содержащем искомую функцию. В этом случае говорят о вариационной форме модели микроуровня. Искомая функция обращает в нуль вариацию функционала, т.е. является его стационарной точкой.
Построение функционала и соответствующей ему вариационной формы модели микроуровня обычно основано на некотором содержательном с физической точки зрения вариационном принципе механики или электродинамики сплошной среды (например, на принципе минимума потенциальной энергии континуальной системы в положении равновесия или на принципе минимума времени прохождения светового луча между двумя точками оптически неоднородной среды). В этом случае стационарная точка функционала соответствует его экстремальному (в частности, минимальному) значению на допустимом множестве функций. Такая форма модели микроуровня, называемая экстремальной вариационной, позволяет, сравнивая значения функционала на любых двух функциях из допустимого множества, оценивать в интегральном смысле близость этих функций к искомой. Это свойство экстремальной вариационной формы модели важно при качественном анализе ММ и при сравнении различных приближенных решений соответствующей краевой задачи*.
При выполнении некоторых ограничений можно построить двойственную вариационную форму модели микроуровня, включающую пару функционалов, достигающих в одной и той же стационарной точке равных между собой альтернативных экстремальных значений (минимума и максимума) . Такая форма ММ дает возможность по разности значений этих Функционалов, вычисленных на некоторой функции из допустимого множества, количественно оценить погрешность, возникающую при выборе этой функции в качестве искомой.
Основной формой динамической (эволюционной) ММ макроуровня являются ОДУ или их системы вместе с заданными начальными условиями. Независимым переменным в таких ММ будет время, а искомыми — фазовые переменные, характеризующие состояние ТО (например, перемещения, скорости и ускорения элементов механических устройств, а также приложенные к этим элементам силы и моменты; давление и расход жидкости или газа в трубопроводе; напряжения и силы тока в электрических цепях и т.п.). В некоторых случаях ММ макроуровня удается представить в интегральной форме, используя принцип Гамильтона — Остроградского или экстремальный вариационный принцип Гамильтона.
Если эволюцию ТО определяет его состояние не только в текущий момент времени t, но и в некоторый предшествующий момент t — τ, то ММ макроуровня включает ОДУ вида
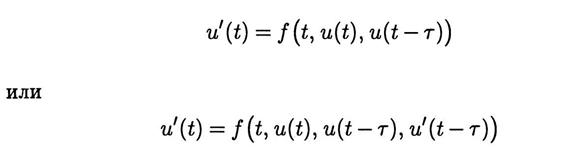
относительно искомой функции u(t). Такие ОДУ называют уравнениями запаздывающего и нейтрального типа соответственно и относят к дифференциально-функциональным уравнениям* (ДФУ) (или дифференциальным уравнениям с отклоняющимся аргументом). Наиболее широко ДФУ и их системы представлены в ММ систем автоматического управления и регулирования. Кроме того, ДФУ находят применение в моделях биологических и экономических процессов.
Запаздывающая реакция ТО на изменение своего состояния может определяться более чем одним интервалом времени 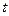 . Тогда ДФУ будет включать не одно, а несколько дискретных запаздываний. В более общем случае запаздывание может быть непрерывным во времени, что приводит, например, для линейной математической модели к интегро-дифференциальному уравнению (ИДУ) вида
. Тогда ДФУ будет включать не одно, а несколько дискретных запаздываний. В более общем случае запаздывание может быть непрерывным во времени, что приводит, например, для линейной математической модели к интегро-дифференциальному уравнению (ИДУ) вида
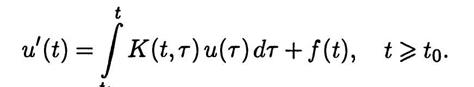
Заданную функцию K(t,r) называют ядром этого ИДУ, а о рассматриваемом ТО говорят, что он обладает памятью, поскольку его эволюция зависит от всей предыстории изменения состояний ТО.
В статическую математическую модель макроуровня не входит время. Поэтому она включает лишь конечное (в общем случае нелинейное) уравнение или систему таких уравнений (в частности, систему линейных алгебраических уравнений — СЛАУ). Такой же вид имеют квазистатическая, стационарная и квазистационарная математические модели макроуровня.
Если для рассматриваемого ТО удается выделить поддающееся количественной характеристике некоторое важное свойство или сочетание таких свойств (надежность, долговечность, массу, стоимость, какой-либо из определяющих качество ТО выходных параметров) и установить их связь с фазовыми переменными при помощи действительной функции, то можно говорить об оптимизации ТО по критерию, выражаемому этой функцией. Ее называют целевой функцией [XIV], поскольку ее значения характеризуют меру (или степень) достижения определенной цели совершенствования ТО в соответствии с выбранным критерием.
Вследствие ограниченности располагаемых ресурсов в реальной ситуации имеют смысл лишь те экстремальные значения целевой функции, которые достигаются в области возможного изменения фазовых переменных ТО, обычно ограниченной системой неравенств. Эти неравенства вместе с целевой функцией и статической ММ ТО в виде конечного нелинейного Уравнения или систем таких уравнений входят в математическую формулировку задачи оптимизации ТО по выбранному критерию, называемой (в общем случае) задачей нелинейного программирования . В частном случае линейной математической модели ТО в виде СЛАУ, линейных целевой функции и неравенств говорят о задаче линейного программирования. К таким задачам обычно приходят при рассмотрении проблем технико-экономического содержания. Задачу оптимизации ТО, описываемого динамической (эволюционной) ММ макроуровня, относят к классу задач оптимального управления .
Для ММ метауровня характерны те же типы уравнений, что и для ММ макроуровня, но эти уравнения включают фазовые переменные, описывающие состояние укрупненных элементов сложных ТО. Если определен закон непрерывного перехода ТО из одного состояния в другое, то для анализа ММ метауровня часто используют аппарат передаточных функций*, а при рассмотрении состояний ТО в дискретные моменты времени ОДУ и их системы переходят в разностные уравнения относительно значений фазовых переменных в эти моменты времени. В случае дискретного множества состояний ТО применяют также аппарат математической логики и конечных автоматов.
| <== предыдущая лекция | | | следующая лекция ==> |
| Акустические свойства горных пород | | | Типологизация социальных проблем |
Дата добавления: 2017-10-09; просмотров: 4400;
