Особенности оценки надежности восстанавливаемых изделий

Восстановление изделий после отказов осуществляется путем ремонта или замены отказавших средств (за исключением программных и информационных). Данные по надежности для восстанавливаемых изделий упрощенно можно представить в виде последовательности моментов времени

t0 < t1 < t2 < ...<tn < ... ,

где t0 – момент включения в работу изделия, элементы выборки с нечетными номерами соответствуют моментам отказов, а с четными – моментам восстановления. Предполагается, что все интервалы времени работоспособности и восстановления являются независимыми случайными величинами со своими законами распределения. Для выборок, цензурированных слева заданным моментом времени, на последнем интервале отсутствует отказ, если это интервал работоспособности, или отсутствует восстановление, если это интервал восстановления. Аналогичные рассуждения следует провести относительно первого интервала изменения работоспособности, если выборка цензурирована справа моментом начала наблюдения. Следует учитывать, что ремонт и замена, вообще говоря, приводят к изменению свойства надежности изделий.

При оценке надежности объектов процесс отказов и восстановлений часто представляют в виде простого процесса восстановле­ния, для которого выборка содержит только моменты отказов или только моменты восстановлений, а функции распределения времени между отказами Fi(t) для всех интервалов одинаковы и равны F(t). Такое представление допустимо, если время восстановления значительно меньше средней наработки между отказами и прово­дится полное восстановление ресурса отказавшего изделия.

Когда отсутствуют априорные сведения о виде закона распределения F(t) применяют непараметрические методы оценки надежности, при этом оценка параметра потока отказов проводится с использованием соотношения

),

где d(t, t+Dt) – количество отказавших изделий в интервале [ t, t+Dt];

n(t) – общее количество эксплуатируемых изделий в момент времени t.

При многократном цензу­рировании в моменты T1, T2, ..., Tm значение n(t) постепенно уменьшается, начиная с исходного значения n1, и определяется по формулам

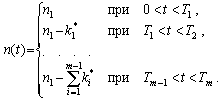
(8.13)

Величина ki* (в отличие от ki для невосстанавливаемых изделий) включает в себя отказавшие и исправные изделия.

Коэффициент оперативной готовности Ког(t, t) для малых значений интервала времени t и при постоянном контроле работоспособности приближенно можно определить как

Ког(t, t) .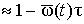

Коэффициент готовности определяется через среднее значение наработки между отказами То и среднее время восстановление Тв по известному соотношению

Кг = То /(То + Тв).

Оценка вероятности отказа в предположении биномиального распределения числа отказавших изделий d(t, t+Dt) соответствует q(t, t+Dt) = d(t, t+Dt)/n(t).

Если восстановление производится на основе "новых" изделий, выработанный ресурс которых не совпадает с ресурсом отказавшего компонента, то вероятность отказа на интервале [t, t+Dt] будет отличаться от предшествующего интервала, за исключением экспоненциального закона распределения (для него интенсивность отказа составляет постоянную величину). В случае различных вероятностей проявления какого-либо события при каждом испытании можно оценить среднюю вероятность события в серии из L испытаний по формуле

,

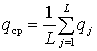где qj – вероятность появления события в j-м опыте. Такой подход предполагает, что полученные оценки показателей надежности являются оценками средних значений этих показателей, определяемых с учетом различных вероятностей отказа изделий в интервале [t, t+Dt].

Восстановление отказавших изделий с использованием "старых" компонентов обусловливает равенство параметра потока отказов значению интенсивности отказов w(t)= l(t).

Параметрические методы применяют при известном законе распределения наработки на отказ. В случае непрерывного контроля работоспособности и мгновенной замены отказавших изделий новыми для некоторых видов законов распределения удается получить ана­литические выражения, определяющие параметр потока отказов:

для экспоненциального распределения w(t)= l ;

для распределения Эрланга (частный случай гамма-распределения, когда параметр d является целым положительным числом)

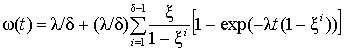
где x=exp(2pj/d), j=(-1)0,5;

для нормального распределения. Функция распределения времени наработки до r-го отказа при s<<m(t) имеет вид

.

Здесь Фл(х) – функция Лапласа (при х>0 Фл(х)=Фн(х)–0,5, где Ф(х) – функции нормального распределения). Параметр потока отказов определяется по формуле

.

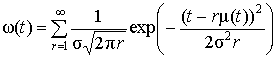Для распределения Вейбулла и общего вида гамма-распределения получить аналитические выражения для показателей надежности не удается, поэтому соответствующие уравнения следует решать численными методами, например, с использованием конечных разностей или разложением уравнений в ряд Фурье.

Рассмотренные подходы и методы решения задач оценки надежности позволяют определить основные показатели для ряда типовых условий эксплуатации. Однако следует учитывать незавершенность исследований в области экспериментального оценивания надежности, наличие других или появление новых моделей с более широкими возможностями, а также моделей, предназначенных для исследования различных аспектов эксплуатации, например, учитывающих периодичность контроля работоспособности или особенности оценки надежности при проведении модернизации изделий.