Однотипные выборки ЭД и задачи их обработки

По результатам эксплуатации может накапливаться целый ряд выборок по однотипным средствам и комплексам. Однотипность не означает равноценности объектов по их показателям. Отличия могут быть обусловлены выпуском изделий различными изготовителями, разнообразием условий применения, в том числе изменением условий в ходе эксплуатации, проведением модернизации и доработками средств. Выборки, характеризующие различные однотипные объекты или один и тот же объект в различные периоды эксплуатации, вообще говоря, могут быть неоднородными. Неоднородность означает, что выборки принадлежат различным законам распределения, которые различаются или только параметрами при одном и том же виде, или видом и параметрами распределения.

Задачи обработки однотипных выборок подразделяются на две группы. К первой группе относятся задачи объединения выборок. Объединение выборок позволяет повысить точность оценок за счет увеличения объема обрабатываемых ЭД. Простое слияние однотипных, но неоднородных выборок для последующей оценки показателей по объединенной выборке, приводит к снижению качества оценок или даже к их полной непригодности. Необходимо применение специальных приемов объединения разнородных сведений в интересах использования всей содержащейся в выборках информации. Таким образом, при объединении выборок необходимо сначала проверить их однородность. Однородные выборки сливаются в одну общую выборку, которая обрабатывается с помощью обычных методов. Неоднородные выборки обрабатываются раздельно или объединяются с помощью специальных приемов.

Вторая группа задач связана с сопоставлением параметров распределения выборок, т.е. с определением существенных различий в значениях параметров однотипных выборок. Наиболее широкое распространение получил один из видов подобного рода задач, так называемый дисперсионный анализ. В дисперсионном анализе исследуются методы проверки гипотезы о равенстве математических ожиданий случайных величин, представленных выборками ограниченного объема. Непосредственное сравнение оценок математических ожиданий совокупности выборок оказывается менее эффективным, чем сопоставление оценок дисперсий, это обстоятельство и дало наименование методу. Подобные задачи возникают при исследовании влияния каких-либо параметров на показатели качества объекта, например: привела ли модернизация оборудования к снижению времени обработки запросов; влияет ли размер кэша второго уровня на производительность системы при решении конкретных задач обработки данных. Эти задачи решаются в рамках однофакторного дисперсионного анализа. В более сложных ситуациях исследуется влияние нескольких факторов на нескольких уровнях (многофакторный дисперсионный анализ). Далее будет рассмотрен только однофакторный анализ.

Итак, пусть имеются выборки по одному устройству, но полученные на различных интервалах времени наблюдений, или имеются выборки по однотипным устройствам, сформированные за один и тот же или различные периоды наблюдений. Количество таких поступивших на обработку выборок т – не менее двух, каждая выборка имеет свой объем пi, i=1, 2, ..., m. Априорных сведений об однородности или неоднородности различных выборок нет.

Следовательно, объектом обработки выступает совокупность независимых выборок результатов наблюдений по одному и тому же показателю однотипных объектов

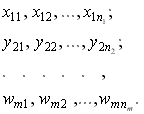
(4.1)

Эта совокупность состоит из m слоев (строк). Каждая i-я строка (i=1, 2, ..., m) представляет собой однородную случайную выборку результатов наблюдений за значениями случайной величины X, Y, … , W соответственно. Слой характеризуется своим, в общем случае векторным, параметром Тi распределения и может иметь свои статистики, т.е. свои функции от выборочных значений.