Объединение выборок
| Прежде, чем объединяться, и для того, чтобы объединиться, необходимо сначала решительно и определенно размежеваться. В.И. Ленин. "Что делать?" . |
По возможности объединения информации из совокупности однотипных выборок можно выделить три типовые ситуации:
различные слои представляют собой однородные выборки. Это является следствием однотипности объектов, близости режимов использования и одинаковости внешних воздействий на исследуемые средства. В такой идеализированной ситуации выборки можно объединить и определять искомые параметры, используя традиционный аппарат математической статистики. Данная ситуация предоставляет наибольшие возможности использования информации, содержащейся в ЭД, именно в таком случае удается достичь максимальной эффективности оценок показателей, т.е. объединение обеспечивает потенциальную возможность полного использования сведений, содержащихся в выборках;
совокупность слоев частично неоднородна. Тогда однородные слои, если таковые обнаружатся, целесообразно объединить, а оставшиеся неоднородные группы выборок обрабатывать раздельно. В этой ситуации всю содержащуюся в выборках информацию полностью извлечь не удается. Однако существуют простые приемы получения некоторых оценок параметров распределения по совокупности неоднородных выборок;
слои полностью или частично неоднородны. Но, в дополнение к результатам наблюдений, имеется априорная информация о взаимосвязи параметров Тi различных выборок. Такие взаимосвязи устанавливаются на основе изучения сущности процессов, протекающих в объектах, и могут задаваться различными способами – в виде аналитических соотношений, ограничений на значения параметров и т. п. Чем выше уровень априорной информированности о взаимосвязях параметров, тем потенциально более высокой эффективности оценок показателей можно достичь.
Следовательно, объединение слоев всегда следует начинать с проверки однородности выборок.
Объединение однородных выборок
Простое объединение рекомендуется только для однородных выборок. Постановка задачи проверки однородности выборок формулируется следующим образом [3].
Имеются результаты наблюдений в виде совокупности выборок типа (4.1), задан уровень значимости a для проверки статистической гипотезы об однородности выборок.
Необходимо проверить однородность слоев.
Допущение: законы распределения случайных величин для различных слоев неизвестны.
Проверка однородности полной расслоенной выборки относительно сложна в реализации и не позволяет выделить те выборки, которые существенно различаются по своим свойствам. Более практично использовать последовательную процедуру проверки и попарного объединения выборок. В качестве исходной выборки можно взять любую, например, первую или наибольшую по количеству элементов. В качестве второй выбирается любая из оставшихся выборок. Эти две выборки проверяются на однородность. При ее наличии выборки объединяются в одну, а при ее отсутствии вторая выборка остается самостоятельной. Указанную проверку и объединение повторяют для всех слоев исходной выборки.
Определение однородности двух выборок проводится на основе проверки статистической гипотезы Н0 о том, что выборки x1, x2, ... , xnx и y1, y1, ... , yny принадлежат одному, пусть и неизвестному, закону распределения. При этом применяют критерии знаков, критерий Вилкоксона (Вилкоксона – Мана – Уитни) и другие. Существенной особенностью критерия знаков является требование равного объема сравниваемых выборок, правда, это требование легко выполнить, "обрезав" при рассмотрении более длинную выборку (но такая операция приводит к потере части информации при сопоставлении выборок). В интересах решения поставленной задачи целесообразно применять второй критерий – критерий Вилкоксона .
Проверка однородности выборок по критерию Вилкоксона состоит в следующем. Пусть для случайной величины Х имеется выборка объема nx и для случайной величины Y выборка объема ny. По этим выборкам необходимо с уровнем значимости a проверить гипотезу Н0 о том, что функция распределения F(x) случайной величин Х равна функции распределения F(y) случайной величины Y. Конкурирующая гипотеза – функции распределения случайных величин различны: F(x)<F(y) или F(x)>F(y), т.е. критическая область двусторонняя.
Сущность проверки основана на простой идее: если верна гипотеза Н0, то нельзя ожидать преобладания наблюдений одной из выборок на любом из концов вариационного ряда, иначе говоря, результаты наблюдений из каждого слоя должны быть рассеяны по всему вариационному ряду. Такая проверка осуществляется только по порядковым соотношениям x>y и x<y между элементами выборок.
Далее считается, что объем первой выборки не превышает объема второй. Если это условие не выполняется, то выборки просто меняются местами. Проверка гипотезы однородности имеет свою специфику для разных объемов выборок.
Пусть nx>3, ny>3 и суммарный объем обеих выборок не превосходит 25. Проверка гипотезы осуществляется поэтапно:
из выборок исклy1ючаются одинаковые элементы (вероятность совпадения элементов весьма невелика, поэтому число исключаемых членов выборок не будет большим);
на основе элементов обеих выборок строится общий вариационный ряд, индексы и конкретные значения элементов можно опустить. В результате получится просто последовательность букв y и x, например xxxyxyyxxxyyy;
подсчитывается сумма порядковых номеров u вариант первой (меньшей по объему) выборки. В приведенном примере nx>ny (nx=7 и ny=6), поэтому первой будем считать выборку для величины Y. Буква y встречается на четвертом, шестом, седьмом, одиннадцатом, двенадцатом и тринадцатом местах, следовательно u=4+6+7+11+12+13=53. Случайная величина u имеет распределение Вилкоксона. Для нее построена специальная таблица нижних критических точек распределения. Фрагмент такой таблицы представлен в табл. П.5;
по таблице критических точек для ny=6, nx=7, заданного уровня значимости, например a=0,05 (критическая область двусторонняя, следовательно, каждая сторона критической области соответствует уровню значимости a/2=0,025), определяется нижняя критическая точка ин. В данном случае ин=27;
вычисляется верхняя критическая точка uв=(ny+nx+1)ny–uн. Для рассматриваемого примера uв=(6+7+1)6–27=57;
если u<uн или u>uв, то нулевую гипотезу отвергают. В противном случае нет оснований для отклонения нулевой гипотезы. В приведенном примере нулевая гипотеза об однородности выборок принимается.
Сумма порядковых номеров вариант первой выборки с увеличением общего объема выборок стремится к нормальному распределению. Нормальное распределение можно применять, если uв>3, ny>3 и объем хотя бы одной из выборок превосходит 25. В таком случае значение нижней критической точки величины u при uв>=ny
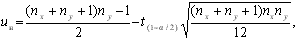
| (4.2) |
где t1–a/2 – квантиль уровня 1-a/2 стандартизованной нормальной случайной величины.
Остальные этапы проверки ничем не отличаются от рассмотренных выше, применительно к малому объему слоев.
В результате выполнения рассмотренных процедур однородные выборки будут объединены.
Объединение неоднородных выборок
Одним из простых и рациональных способов слияния является линейное объединение оценок показателей независимо от степени однородности имеющейся информации. При таком способе объединения неоднородной информации общая выборка рассматривается как смесь из m выборок однотипных наблюдений, каждая из которых имеет свои значения показателей. Подобное объединение возможно для несмещенных выборочных средних оценок (типа центральных моментов распределения, вероятностей свершения событий).
Пусть имеются выборочные средние оценки qi отдельных слоев. Задача состоит в нахождении функции 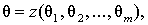 которая была бы лучшей, в смысле принятого критерия, объединенной оценкой q параметра Т. Типичным критерием оптимальности оценки является минимум дисперсии оценки. В качестве оценочной функции можно взять любую, но использование сложных функций вызывает трудно преодолимые препятствия по нахождению несмещенных и эффективных оценок. Лучше взять простую линейную комбинацию
которая была бы лучшей, в смысле принятого критерия, объединенной оценкой q параметра Т. Типичным критерием оптимальности оценки является минимум дисперсии оценки. В качестве оценочной функции можно взять любую, но использование сложных функций вызывает трудно преодолимые препятствия по нахождению несмещенных и эффективных оценок. Лучше взять простую линейную комбинацию
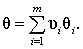
Коэффициенты ui выбирают из условия
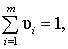
что обеспечивает получение несмещенной объединенной оценки. Значения коэффициентов ui, обеспечивающие минимум дисперсии искомой оценки 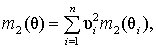 равны
равны 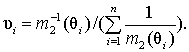
Применение рассмотренного подхода предполагает знание дисперсий оценок, которые, как правило, неизвестны. Замена дисперсии ее выборочной оценкой приводит к трудно оцениваемому смещению величины q. Преодоление данного недостатка возможно на основе объединения выборок с учетом доли каждой выборки в общем объеме имеющихся сведений, т.е. коэффициенты характеризуют относительный вклад каждого слоя в общую оценку. Значение коэффициента ui можно определить как отношение объема данной выборки к общему объему всех наблюдений или по отношению наработки данной группы устройств к общей наработке всех устройств. Линейное объединение оценок приводит к их усреднению по всем выборкам. Иначе говоря, значение некоторого показателя в данном случае следует рассматривать как среднее значение случайной величины, принимающей значение qi с вероятностью ui.
В некоторых случаях выборки формируются по наблюдениям за аналогичными объектами, работающими в различных условиях, и из априорных соображений (например, по результатам математического моделирования) известна функциональная связь между параметрами этих выборок или установлена зависимость показателя каждого объекта от условий его функционирования. Наличие таких соотношений позволяет построить искомые оценки показателей по методу максимального правдоподобия, используя объединенную выборку.
Сущность подхода состоит в следующем. Пусть имеются две выборки, являющиеся реализациями случайных величин X и Y, принадлежащих различным законам распределения. Так как изделия подобны, то параметры qx и qy связаны между собой функциональной зависимостью qy=j(qx), вид которой предполагается известным. Тогда логарифм функции правдоподобия запишется в виде
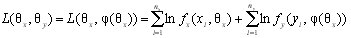 , ,
| (4.3) |
где fx и fy – функции плотности распределения случайных величин X и Y соответственно. В таком случае задача оценивания двух параметров сводится к задаче оценивания параметра qx по одной совместной выборке x1, x2, ... , xn, y1, y2, ... , ym..По методу максимума правдоподобия оценка qx находится из уравнения
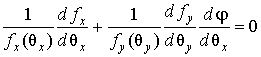 .
.
Эта оценка обладает всеми достоинствами оценок максимального правдоподобия, но нахождение оценки связано с преодолением математических трудностей, связанных с решением уравнения правдоподобия. Если не вводить существенных упрощений по виду функциональной связи параметров, то обычно уравнение удается решить только численными методами.
В настоящее время нет достаточно обоснованных и проработанных общих подходов к объединению информации, содержащейся в неоднородных выборках. Подобное объединение было бы возможно, если бы удалось построить модели, учитывающие взаимосвязи показателей с процессами, протекающими в конкретных объектах и во внешней среде, или удалось бы установить корреляционные связи показателей объектов, эксплуатируемых в различных условиях. При отсутствии объективных априорных сведений по этим закономерностям можно предусмотреть их «открытие» на основе обработки эмпирических данных. Но такая процедура требует значительного объема статистического материала.
Пример 4.1.По результатам наблюдения за пропускной способностью канала в различные дни испытаний сформированы упорядоченные выборки, табл. 4.1. При уровне значимости a = 0,05 необходимо проверить однородность выборок.
Решение. Возьмем в качестве исходной выборку Х, соответствующую первому дню испытаний, и проверим ее на однородность с выборкой Y, составленной из результатов второго дня испытаний. Перечислим последовательность элементов в общем вариационном ряду, составленном из элементов первой и второй выборки: yyxyxyxxyxyxy .
Таблица 4.1
| День испытаний | Пропускная способность, байт/с | ||||||
| 259,14 | 260,06 | 260,97 | 262,43 | 267,83 | 273,14 | ||
| 253,68 | 258,14 | 259,49 | 260,18 | 263,65 | 271,39 | 274,12 | |
| 256,69 | 259,36 | 262,84 | 265,94 | 270,33 | 270,44 | 271,63 |
Сумма порядковых номеров вариант первого дня испытаний (n1<n2) составит
u=3+5+7+8+10+12=45.
Количество элементов в обеих выборках меньше 25, поэтому следует воспользоваться распределением Вилкоксона для проверки гипотезы Н0 об однородности выборок. Значение нижней критической точки для двусторонней критической области при заданном уровне a/2=0,025, количестве наблюдений п1=6, п2=7 определим по табл. П.5. Оно составит uн=27. Значение верхней критической точки распределения равно
uв=(п1+п2+1)п1–uн=(6+7+1)6–27=57.
Значение величины u превышает uн и меньше uв, поэтому нет оснований отвергать нулевую гипотезу об однородности выборок. Обозначим объединенную выборку через Х .
Проверим однородность объединенной выборки Х и результатов третьего дня наблюдений W. Построим общий вариационный ряд из элементов выборки Х и выборки W: xwxxwxxxxxwxwxwwxwxx.
Сумма порядковых номеров вариант третьего дня испытаний (этих вариант меньше, чем в объединенном ряду Х) составит
u=2+5+11+13+15+16+18=80.
Воспользуемся распределением Вилкоксона и определим при уровне значимости a/2=0,025, п1=7, п2=13 нижнюю критическую точку uн=48, табл. П.5. Верхняя критическая точка
uв=(7+13+1)7–48=99.
В соответствии с выбранным критерием нет оснований отвергать нулевую гипотезу, следовательно, все три выборки однородны и их можно объединить в одну.
Дата добавления: 2017-10-09; просмотров: 1673;
