Основная формула трансформаторной ЭДС

Возьмем катушку с ферромагнитным сердечником и вынесем отдельным элементом омическое сопротивление обмотки как это показано на рис.2.8[3].

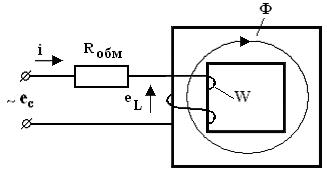
Рисунок 2.8 – К выводу формулы трансформаторной ЭДС

При включении переменного напряжения e_c в катушке, cогласно закону электромагнитной индукции, возникает ЭДС самоиндукции е_L.

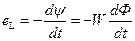(2.8)

где ψ – потокосцепление,

W – число витков в обмотке,

Ф – основной магнитный поток.

Потоком рассеяния пренебрегаем. Приложенное к катушке напряжение и наведённая ЭДС уравновешиваются. По второму закону Кирхгофа для входной цепи можно записать:

е_c + е_L = i * R_обм, (2.9)

где R_обм – активное сопротивление обмотки.

Поскольку е_L >> i * R_обм , то падением напряжения на омическом сопротивлении пренебрегаем, тогда е_c ≈ – 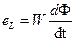. Если напряжение сети гармоническое е_с = E_m cos ωt, то E_m cos ωt = 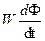, откуда 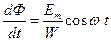. Найдём магнитный поток. Для этого берём неопределённый интеграл от правой и левой частей. Получаем

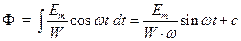, (2.10)

но так как магнитопровод считаем линейным, в цепи протекает только гармонический ток и нет постоянного магнита или постоянной составляющей, то постоянная интегрирования с = 0. Тогда дробь перед гармоническим множителем есть амплитуда магнитного потока 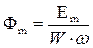, откуда выразим E_m = Ф_m*W*ω. Его действующее значение равно

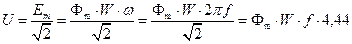или получаем

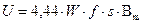(2.11)

где s – сечение магнитопровода (сердечника, стали).

Выражение (2.11) называют основной формулой трансформаторной ЭДС, которая справедлива только для гармонического напряжения. Обычно её видоизменяют и вводят так называемый коэффициент формы, равный отношению действующего значения к среднему:

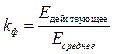. (2.12)

Найдем его для гармонического сигнала, но среднее значение находим на интервале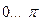

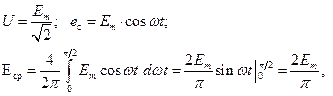
Тогда коэффициент формы равен 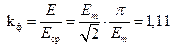и основная формула трансформаторной ЭДС принимает окончательный вид:

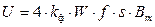(2.13)

Если сигнал меандр, то амплитудное, действующее и среднее значения за половину периода равны между собой и его 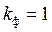. Можно найти коэффициент формы и для других сигналов. Основная формула трансформаторной ЭДС будет справедлива.

Построим векторную диаграмму катушки с ферромагнитным сердечником. При синусоидальном напряжении на зажимах катушки её магнитный поток тоже синусоидальный и отстаёт по фазе от напряжения на угол π/2 как показано на рис.2.9а.

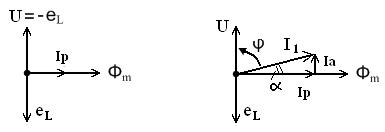
а) б)

Рисунок 2.9 – Векторная диаграмма катушки с ферромагнитным

сердечником а) без потерь; б) с потерями

В катушке без потерь намагничивающий ток – реактивный ток ( I_p ) совпадает по фазе с магнитным потоком Ф_m. Если имеют место потери в сердечнике ( 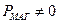), то угол 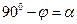– угол потерь на перемагничивание сердечника. Активная составляющая тока I_а характеризует потери в магнитопроводе.