ЛДС с конечной и бесконечной импульсной характеристикой

Определим особенности импульсных характеристик рекурсивных и нерекурсивных ЛДС.

Учтем, что импульсная характеристика – это реакция на единичный дискретный импульс.

В результате замены в разностном уравнении входного сигнала на единичный дискретный импульс 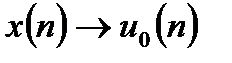, получим выражение для импульсной характеристики нерекурсивной ЛДС:

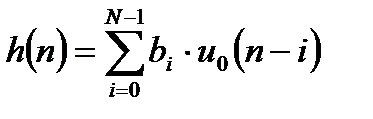
или в соответствии с определением единичного дискретного импульса

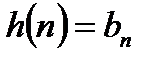. (2.1)

Соответственно, передаточная функция ЛДС с конечной импульсной характеристикой имеет следующий вид:

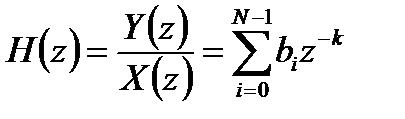. (2.2)

Таким образом, можно сделать следующие выводы:

- импульсная характеристика нерекурсивной ЛДС имеет конечную длительность, а значения отсчетов импульсной характеристики равны коэффициентам 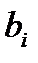разностного уравнения;

- нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ, finite impulse response – FIR);

- передаточная характеристика нерекурсивной ЛДС не имеет полюсов;

- вследствие отсутствия обратных связей и полюсов передаточной функции любой нерекурсивный фильтр является устойчивым.

Простота анализа и реализации, абсолютная устойчивость нерекурсивных ЛДС привели к их широкому использованию на практике. Достоинством нерекурсивных ЛДС является возможность получения линейных фазочастотных характеристик. Однако для получения частотных характеристик с высокой прямоугольностью АЧХ необходимы фильтры высокого порядка – до нескольких сотен и даже тысяч.

Импульсная характеристика рекурсивного фильтра рассчитывается значительно сложнее. Ранее было аналитически получено, что импульсная характеристика рекурсивного фильтра с полюсами в передаточной функции описывается бесконечными степенными рядами:

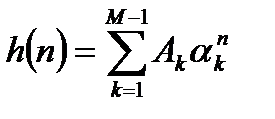. (2.3)

где 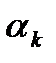- полюс;

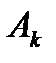- коэффициент разложения при k-м полюсе.

Передаточная функция рекурсивной ЛДС описывается передаточной дееюей ЛДС общего вида:

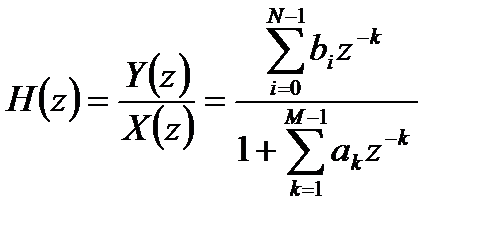, (2.4)

и ее эквивалентными формами записи через произведение сомножителей и в виде суммы простых дробей:

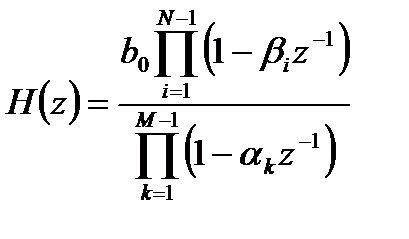, (2.5)

где 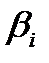- нули, 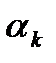- полюса;

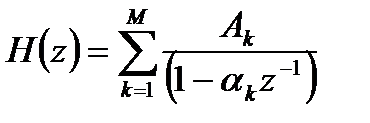, (2.6)

где 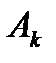- коэффициент разложения при k-м полюсе.

Таким образом, можно сделать следующие выводы:

- наличие в схеме расчетов рекурсивного фильтра обратных связей позволяет получить бесконечную импульсную характеристику;

- рекурсивные фильтры также называются фильтрами с бесконечной импульсной характеристикой (БИХ, infinite impulse response – IIR);

- передаточная функция рекурсивных фильтров всегда имеет полюса;

- из-за наличия обратных связей и полюсов передаточной функции рекурсивные фильтры могут быть неустойчивыми.

Достоинством рекурсивных фильтров является высокая крутизна спадов АЧХ даже при малом порядке фильтра. Недостатком рекурсивных фильтров является нелинейность фазочастотной характеристики.