Кинетическая энергия
Кинетическая энергия точки и системы. Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 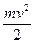 или
или 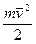 , так как скалярный квадрат любого вектора равен квадрату модуля этого вектора. Кинетическая энергия является скалярной положительной величиной.
, так как скалярный квадрат любого вектора равен квадрату модуля этого вектора. Кинетическая энергия является скалярной положительной величиной.
Кинетической энергией системы 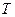 называют сумму кинетических энергий всех точек механической системы, т. е.
называют сумму кинетических энергий всех точек механической системы, т. е.
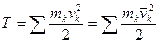 . (200)
. (200)
Кинетическая энергия как точки, так и сие темы не зависит от направления скоростей точек. Кинетическая энергия может быть равна нулю для системы только при условии, если все точки системы находятся в покое.
Вычисление кинетической энергии системы (теорема Кёнига): Кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс:
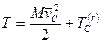 , (201)
, (201)
где 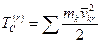 .
.
Величина 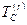 – кинетическая энергия относительного движения системы относительно системы координат, движущейся поступательно вместе с ее центром масс, или кинетическая энергией системы относительно центра масс.
– кинетическая энергия относительного движения системы относительно системы координат, движущейся поступательно вместе с ее центром масс, или кинетическая энергией системы относительно центра масс.
Кинетическая энергия твердого тела. При поступательном движении твердого тела
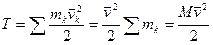 , (202)
, (202)
так как при поступательном движении твердого тела скорости всех точек тела одинаковы, т. е. 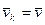 , где
, где 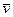 – общая скорость для всех точек тела.
– общая скорость для всех точек тела.
Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе всего тела.
При вращении тела вокруг неподвижной оси
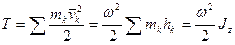 , (203)
, (203)
где 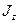 – момент инерции тела относительно оси вращения
– момент инерции тела относительно оси вращения 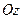 .
.
Следовательно, кинетическая энергия тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
При плоском движении твердого тела
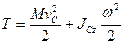 . (204)
. (204)
Таким образом, при плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.
Дата добавления: 2017-09-19; просмотров: 534;
