Пересечение прямой линии с плоскостью .

Рассмотрим общий случай пересечения прямой с плоскостью, когда и плоскость и прямая общего положения.

На рис. 4.16. дана плоскость треугольник АВС и прямая l.

Определить точку пересечения К. Алгоритм решения задачи:

1. Прямую l заключаем вспомогательную проецирующую плоскость, в нашем случае, горизонтально проецирующую å ^ p₁ l₁ º å₁.

2. Строим линию пересечения данной плоскости и вспомогательной åÇ(АВС)®(12).

3. Определяем искомую точку на пересечение линии пересечения и проекции прямой l (1₂2₂) Ç l₂ ® K₂ ® K₁.

4. Определяем видимость прямой l относительно точки пересечения.

Т.к. стороны треугольника АВС и прямой l являются скрещивающимися прямыми, видимость определяем по конкурирующим точкам.

Если в задаче на определение точки встречи прямой линии с плоскостью один из геометрических объектов – частного положения, то в ведение вспомогательной плоскости не требуется. Рассмотрим эти случаи.

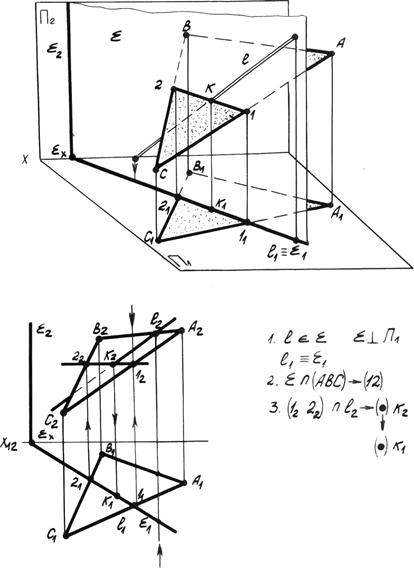
Рис. 4.16. Пересечение прямой линии с плоскостью.

Задача: Дана плоскость (СDЕ) – горизонтально проецирующая и прямая линия l общего положения (рис. 4.17а) Определить точку их пересечения.

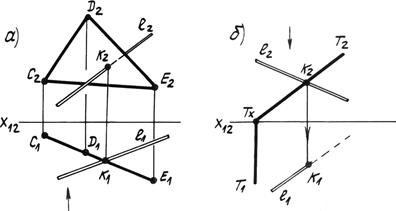
Рис. 4.17.

Решение: Так как треугольник CDE – горизонтально проецирующая плоскость и проецируется на p₁ в прямую линию, то пересечение прямой l определяем на пересечении горизонтальных проекций объектов в единственной точке К₁. Далее определяем видимость прямой l относительно точки пересечения К.

Аналогично решаем задачу на рис. 4.17б, где плоскость Т задана следами и является фронтально проецирующей.

Задача: Дана плоскость (AВC) – общего положения и фронтально проецирующая прямая l. Определить точку их пересечения (рис. 4.18а).

Решение: Так как прямая l является фронтально проецирующей и проецируется на плоскость p₂ в точку, то фронтальная проекция точки пересечения К₂ совпадает с l₂. Горизонтальную проекцию точки пересечения К₁ определяем из условия принадлежности точки К и прямой l плоскости АВС. Проводим вспомогательную прямую (12), принадлежащую плоскости, через К₂. Рассматриваем видимость прямой l относительно точки пересечения К. Аналогично решаем задачу на рис. 4.18б, где плоскость Г задана следами, а прямая l перпендикулярна плоскости p₁.

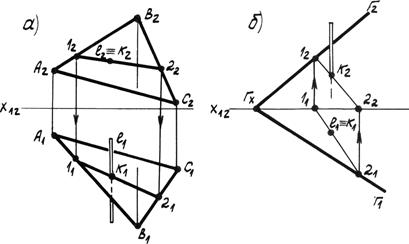
рис. 4.18.