Модель магнитного материала

Математическое моделирование в Elcut

Пакет ELCUT, (ПК ТОР, Санкт-Петербург) известен на рынке с 1990 года как интерактивный инструмент для расчета двумерных магнитных, электрических, температурных полей, а также полей упругих напряжений и деформаций. ELCUT решает задачи, описываемые уравнениями Лапласа, Пуассона и диффузии в плоско-параллельных и осесимметричных расчетных областях произвольной формы.

При решении нестационарных задач электромагнитного поля и теплопередачи, начальным условием может быть нулевой потенциал или результат решения другой задачи. Шаг интегрирования по времени назначается вручную или выбирается автоматически адаптивным алгоритмом.

ELCUT способен использовать решение одной задачи в качестве источника для другой. Так, например, распределение вихревых токов, являющееся результатом решения электромагнитной задачи, может быть использовано как источник тепловой мощности (омических потерь) для тепловой задачи, а ее результат – распределение температуры – послужит для расчета термических деформаций в задаче упругости.

Метод решения

ELCUT использует метод конечных элементов. Разработчиками выбран единственный тип конечного элемента – линейный треугольник. Все усилия создателей, сосредоточены на том, чтобы эффективно работать с огромным числом простых треугольных элементов. Эксперимент показал успешное решение задачи с сеткой, превышающей 5 млн. степеней свободы (около 10 млн. треугольных элементов) за 12 мин на обычном офисном персональном компьютере (2.6 ГГц, 1.5 Гбайт памяти).

Использование метода конечных элементов позволяет практически снять ограничения на сложность расчетной области, свойства материалов и пр. В состав ELCUT входит эффективный геометрический редактор, который позволяет нарисовать мышью геометрию расчетной области за считанные минуты. Возможен также импорт геометрии или отдельных фрагментов из программ САПР. В редактор встроен генератор сетки конечных элементов, который может работать как в полностью автоматическом режиме, так и учитывать пожелания пользователя о густоте сетки в отдельных местах модели. Имеется процедура адаптивного уточнения густоты сетки на базе апостериорной оценке погрешности грубого решения.

Ключевым моментом эффективности является процедура решения результирующей системы линейных алгебраических уравнений (СЛАУ). Как известно, манипулирование с большой разреженной матрицей, характерной для метода конечных элементов, требует разработки алгоритмов, тесно связанных с эффективной схемой хранения матрицы в оперативной памяти. ELCUT использует собственную систему алгоритмов и схемы хранения, названную "метод геометрической декомпозиции". Это один из вариантов метода сопряженных градиентов, с эвристическим блочно-диагональным предобуславливателем, учитывающим физическую природу задачи. Метод демонстрирует уникальную скорость решения, растущую с увеличением количества степеней свободы почти линейно (точнее, в степени 1.1).

Модель магнитного материала

В задачах магнитостатики и нестационарного магнитного поля ELCUT использует следующую модель материала. Линейный материал характеризуется численным значением относительной магнитной проницаемости, причем, для учета анизотропии могут быть заданы две константы (по оси X и по оси Y, либо в радиальном и тангенциальном направлении).

Нелинейные материалы, у которых магнитная проницаемость зависит от величины поля, рассматриваются только как изотропные. В этом случае, пользователь задает по точкам основную кривую намагничивания, которая автоматически аппроксимируется кубическим сплайном. Для магнитотвердых материалов дополнительно задается вектор коэрцитивной силы по индукции (в том числе и направленный радиально или тангенциально), который сдвигает основную кривую намагничивания во второй квадрант.

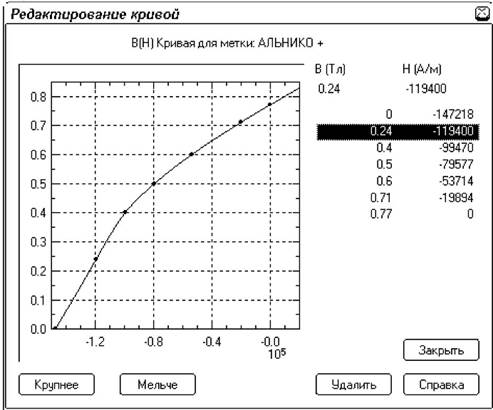
Рис. 1. Кривая размагничивания сплава типа Алнико