Соотношение порядка и беспорядка в природе
При изложении статистических закономерностей в природе упоминалось, что любая замкнутая макроскопическая система, т.е. система не обменивающаяся с окружающей средой веществом и энергией, с течением времени эволюционирует к состоянию статистического равновесия (о нем также говорят как о термодинамическом или тепловом равновесии), когда макроскопические физические величины с большой относительной точностью равны своим средним значениям. Таким образом, в состоянии статистического равновесия отсутствуют какие-либо макроскопические структуры, т.е. это состояние неупорядоченное, хаотическое. Замкнутые системы всегда эволюционируют к хаосу - состоянию, в котором полностью отсутствует какое-либо регулярное движение и регулярные структуры. Причиной этого является то, что состояние статистического равновесия является наиболее вероятным из всех различных состояний системы. Как уже упоминалось, мерой беспорядка состояния системы является физическая величина, называемая энтропией, и, таким образом, эволюция макроскопической системы в состояние статистического равновесия связана с законом возрастания энтропии замкнутой системы.
Как может показаться, закон возрастания энтропии утверждает, что в природе должны существовать лишь процессы, в которых происходит разрушение упорядоченных структур и переход от порядка к хаосу. Такие процессы действительно наблюдаются в природе, можно привести достаточно много примеров. Капля чернил, попавшая в воду, постепенно растворяется во всем объеме воды, так что вместо первоначальной структуры (капли) образуется однородная бесструктурная смесь. Горные породы под воздействием ветра, влаги и температуры разрушаются, и рельеф местности выравнивается. Ударная волна (упорядоченная во времени структура), образующаяся в результате электрического разряда - молнии (а также в результате выстрела или взрыва), по мере распространения размывается и вместо резкого хлопка вблизи разряда мы слышим гулкие раскаты на большом расстоянии от него. Берега искусственных водохранилищ постепенно размываются, а вместо первоначальных островов образуются отмели. Пожары уничтожают леса.
Однако наряду с такими процессами в природе существуют и противоположные им, а именно процессы, связанные с образованием структур из хаоса. Такие процессы называются также процессами самоорганизации. Наиболее явственно и наглядно такие явления демонстрирует живая природа. Из семечка, посаженного в землю может вырасти большое растение со сложной структурой (ствол, ветви, листья, цветы) и вся огромная (по сравнению с первоначальным семечком) масса этого растения образуется из бесструктурного вещества (вода, углекислый газ, элементы почвы). На первый взгляд такие процессы настолько отличаются от процессов в неживой природе, где в основном проявляются процессы разрушения структур, что долгое время существовало мнение о неприменимости законов физики к описанию живой природы. Тем не менее, более пристальный взгляд дает достаточно много примеров процессов самоорганизации в неживой природе.
Всем знакомые снежинки, обладающие прекрасной высокосимметричной структурой, образуются из бесструктурного водяного пара. В разные дни небо может быть затянуто пеленой облачности, хаотическими облаками (представляющими, тем не менее, определенные структуры), а также и симметричными (в смысле повторяемости) волнами облаков. В спокойном течении реки при огибании препятствий или при ускорении течения в области сужения русла могут возникнуть структуры в виде вихрей.
Классическим примером образования структур из полностью хаотической фазы в лабораторных условиях являются ячейки Бенара.
В 1900 г. была опубликована статья Ч. Бенара с фотографией структуры, по виду напоминавшей пчелиные соты (рис. 16.1). Эта структура образовалась в ртути, налитой в плоский широкий сосуд, подогреваемый снизу, после того, как перепад температуры между верхним и нижним слоем жидкости превысил некоторое критическое значение. Весь слой ртути (то же происходит и с другой вязкой жидкостью, например, растительным маслом) распадался на одинаковые вертикальные шестигранные призмы с определенным соотношением между стороной и высотой - ячейки Бенара. В центральной области призмы жидкость поднимается, а вблизи вертикальных граней - опускается. В поверхностном слое жидкость растекается от центра к краям, в придонном - от границ призм к центру. По сравнению с однородным состоянием такие конвективные ячейки, очевидно, являются более высокоорганизованной структурой.
Примерами образования структур являются автоколебания. Звуковые автоколебания возникают в смычковых и некоторых духовых инструментах, когда равномерное (бесструктурное по времени) движение смычка или струи воздуха приводят к возникновению периодической волны (то, что звуки производит живой человек не является принципиальным, завывания ветра также являются подобными автоколебаниями). Электрические или электромагнитные автоколебания образуются в генераторах электрических сигналов, используемых в радио, телевидении, компьютерах, а также в оптических квантовых генераторах –
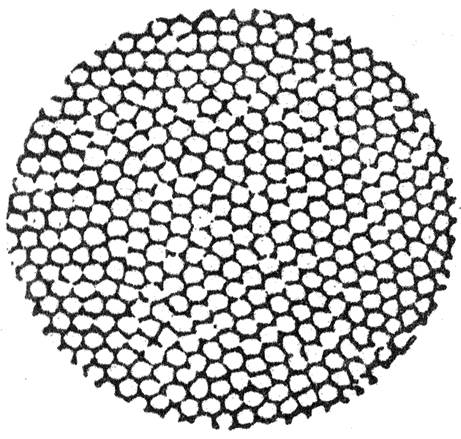
Рис. 16.1. Ячейки Бенара (упорядоченная конвекция в тонком слое масла при неоднородном нагревании)
лазерах. Автоколебания в механических часах, вообще говоря, самопроизвольно не возникают, однако, при соответствующих условиях, например, если часы-ходики поместить на ветру, такая автогенерация становится возможной (далее мы еще вернемся к этому примеру, так как на нем хорошо видна причина самоорганизации).
Автоколебания возникают и при некоторых химических процессах. Классическим примером химической реакции этого типа является реакция Белоусова - Жаботинского, наблюдавшаяся в смеси серной кислоты, малоновой кислоты, сульфата церия (Се) и бромида калия. В процессе этой реакции ионы Се4+, находящиеся в растворе, периодически превращаются в ионы Се3+ и затем обратно. Внешне это проявляется в периодическом изменении цвета раствора. В зависимости от концентрации растворенных веществ период колебаний варьируется от 2 до 100 с.
Естественно, автоколебания присущи не только неживой природе. В живой же природе они происходят как на уровне организма - биение сердца, периодическое непроизвольное сокращение мышц и т.д., так и на более высоком уровне, например на уровне биогеоценоза. Примером являются синхронные колебания популяций кроликов и рысей, наблюдавшиеся, в частности, на протяжении 100 лет в Канаде.
До сих пор говорилось о макроструктурах, т.е. о структурах в макромире. Однако структуры наблюдаются и в мегамире. Поскольку время образования таких структур значительно превышает время существования человеческой цивилизации, мы не можем наблюдать их самообразование. Наблюдаются лишь процессы разрушения, например, взрыв сверхновой и образование на ее месте Крабовидной туманности. Тем не менее современные гипотезы, подтвержденные расчетами в рамках соответствующих математических моделей, говорят о том, что структуры мегамира также образовались из однородного на начальной стадии вещества Вселенной, а процесс образования таких структур продолжается и в настоящее время.
Из приведенных примеров следует, что процессы самоорганизации существуют как в живой, так в неживой природы. Более того, такие процессы выходят за рамки объектов, исследуемых естественными науками, и проявляются и в обществе, живущем по социальным законам. Бесструктурное при первобытнообщинном строе общество в ходе истории трансформировалось в общество со многими иерархическими структурами и объединениями. Автоколебания возникают в экономике и проявляются в виде периодических подъемов и спадов производства.
Таким образом, процессы самоорганизации являются достаточно типичным свойством нашего мира, а следовательно, должны подчиняться и некоторым общим законам. Это означает, что математические уравнения, описывающие эти процессы, должны иметь нечто общее. Однако до последнего времени исследование таких задач было затруднено ввиду чрезвычайной сложности соответствующих уравнений. И даже в том случае, когда исходные уравнения выглядят просто, получить их решения, описывающие процессы самоорганизации (например, образование вихрей в движущейся жидкости), часто является непосильной задачей. Вот что пишет лауреат Нобелевской премии по физике Р. Фейнман: «В простейшей форме задача такова: пропустим через очень длинную трубку на большой скорости воду. Спрашивается: какое нужно давление, чтобы прогнать сквозь трубку данное количество воды? И никто, основываясь только на первичных законах и на свойствах самой воды, не умеет ответить на этот вопрос. Если вода течет неторопливо или когда сочится вязкая жижа вроде меда, то мы прекрасно все умеем. Ответ вы можете найти, например, в любом вашем учебнике. А вот с настоящей, мокрой водой, брызжущей из шланга, справиться мы не в силах».
Тем не менее, в последнее время ученые начинают активно исследовать такие задачи, что, в частности, объясняется их важностью в силу универсального характера. И хотя успехи в этом направлении более чем скромны по сравнению, например, с исследованиями в физике микромира, многие качественные особенности такого рода задач становятся понятными. Соответствующее научное направление выделилось в отдельную область, для которой Г. Хакен (1973 г.) предложил название синергетика. Предметом этой новой области науки было названо изучение общих принципов функционирования систем, в которых из хаотических состояний самопроизвольно возникают упорядоченные пространственные, временные и пространственно-временные структуры. Синергетика призвана построить физическую модель этих процессов и подобрать для их описания адекватный математический аппарат. Не ставя целью изложение соответствующей теории, рассмотрим качественные особенности систем, в которых происходят процессы самоорганизации и обсудим причины, приводящие к возникновению структур в этих системах.
Дата добавления: 2017-09-19; просмотров: 262;
